3.1 数字类型及操作
3.1.1整数
特点:可正可负
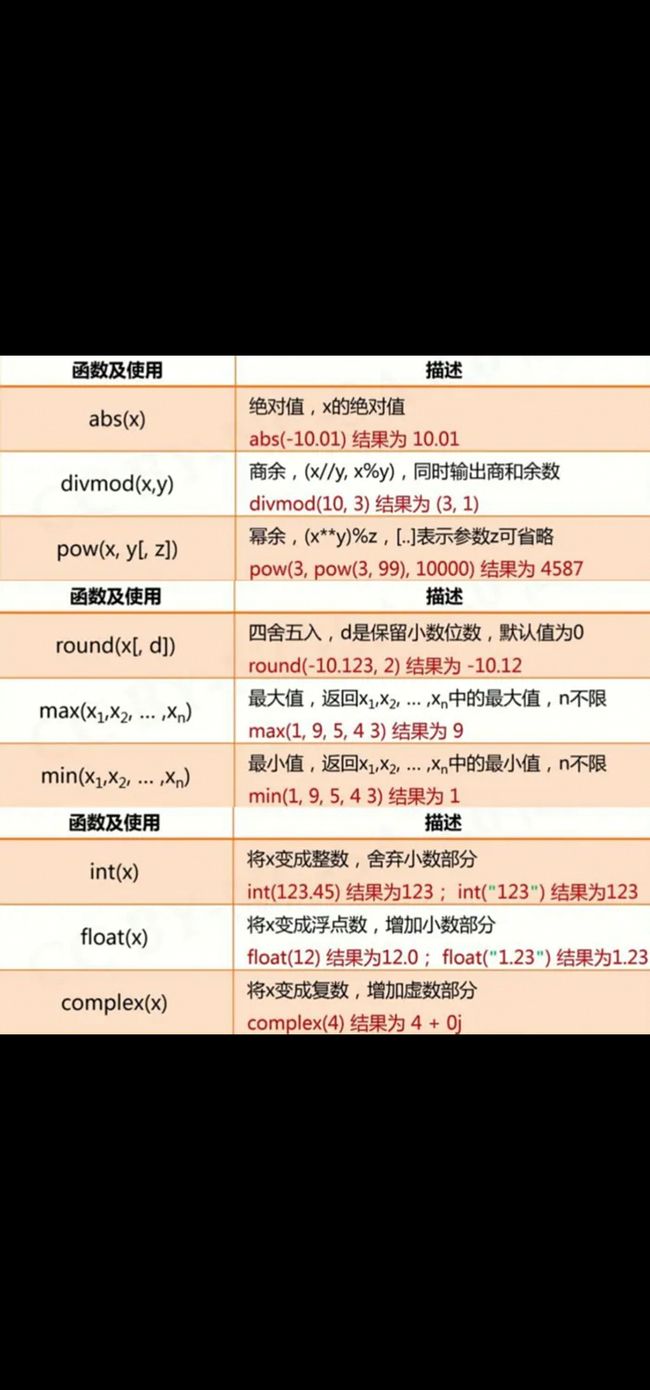
pow(x,y)用来计算x的y次方
四种进制:1 十进制:1010,999,-876
2 二进制:OB或ob开头,比如ob010
3八进制:0o或者0O开头,比如:0O123
4十六进制:0x或者0X开头,比如:0x76
3.1.2 浮点数
定义:带有小数或者小数点的数字
特点:取值范围和小数精度都存在限制,但常规计算中可以忽略不计,若运算中出现不确定常数为正常现象。
==在Python中是一种等于的判断符号
round(x,d)表示对x四舍五入去第d位小数为止
科学计数法:使用字母e或者E,e表示a*10的b次方
3.1.3 复数
定义:a+bj a为实部 b 为虚部
z.real取实部
z.imag取虚部
3.1.4 数值运算操作符
3.1.5数值运算函数
3.2 天天向上的力量
3.2.1 问题一
每天进步千分之一,每天退步千分之一,一年后的变化?
#DayDayUpQ1.py
Dayup=pow(1.001,365)
Daydown=pow(0.999,365)
print("向上:{:.2f},向下:{.:2f}".format(Dayup,Daydown))
3.2.2 问题二
每天努力千分之五,每天退步千分之五,一年后的变化
#DayDayUpQ2.py
dayfactor=0.005
dayup=pow(1+dayfactor,365)
daydown=pow(1-dayfactor,365)
print("向上:{:.2f},向下:{:.2f}".format(dayup))
3.2.3 问题三
工作日每天进步百分之一,休息日每天退步百分之一,一年后的变化
#DayDayUpQ3.py
dayup=1.0
dayfactor=0.01
for i in range(365):
if i% 7 in [6,0]:
dayup=dayup*(1-dayfactor) else:
dayup=dayup*(1+dayfactor)
print("工作的力量:{:.2f}".format(dayup))
3.2.4 问题四
如果只有工作日努力需要努力多少才能比得上每天努力的人
#DayDayUpQ4.py
def dayUp(df):
dayup=1
for i in range(365):
if i% 7 in [6,0]:
dayup=dayup*(1-0.01)
else:
dayup=dayup*(1+df)
return dayup
dayfactor=0.01
while dayUp(dayfactor)<37.78:
dayfactor+=0.001
print("工作日的努力为:{:.3f}".format(df))
3.3 字符串问题及操作
3.3.1 字符串类型的表是字符的有效序列,可对其中的字符进行索引,从零开始。
表达方式:有两类四种表达方式 " " 或者 ' ' 或者 " ' " 或者 ' " ' 或者 ''' " ' '''
字符串的序号:正向递增序列以及反向递减序列
字符串的索引:返回字符串中的单个字符 <字符串>[M]
字符串的切片:返回字符串中的多个字符 <字符串> [M:N]
字符串的序号:正向递增序列以及反向递减序列示
定义:由0个或者多个字符组成的有序字符序列,由一对单引号或者双引号表示。
3.2 天天向上的力量
3.2.1 问题一
每天进步千分之一,每天退步千分之一,一年后的变化?
#DayDayUpQ1.py
#DayDayUpQ1.py
Dayup=pow(1.001,365)
Daydown=pow(0.999,365)
3.2.2 问题二
每天努力千分之五,每天退步千分之五,一年后的变化
#DayDayUpQ2.py
dayfactor=0.005
dayup=pow(1+dayfactor,365)
daydown=pow(1-dayfactor,365)
print("向上:{:.2f},向下:{:.2f}".format(dayup))
3.2.3 问题三
工作日每天进步百分之一,休息日每天退步百分之一,一年后的变化
#DayDayUpQ3.py
dayup=1.0
dayfactor=0.01
for i in range(365):
if i% 7 in [6,0]:
dayup=dayup*(1-dayfactor)
else:
dayup=dayup*(1+dayfactor)
print("工作的力量:{:.2f}".format(dayup))
3.2.4 问题四
如果只有工作日努力需要努力多少才能比得上每天努力的人
#DayDayUpQ4.py
def dayUp(df):
dayup=1
for i in range(365):
if i% 7 in [6,0]:
dayup=dayup*(1-0.01)
else:
dayup=dayup*(1+df)
return dayup
dayfactor=0.01
while dayUp(dayfactor)<37.78:
dayfactor+=0.001
print("工作日的努力为:{:.3f}".format(df))
3.3 字符串问题及操作
3.3.1 字符串类型的表示
定义:由0个或者多个字符组成的有序字符序列,由一对单引号或者双引号表示。
是字符的有效序列,可对其中的字符进行索引,从零开始。
表达方式:有两类四种表达方式 " " 或者 ' ' 或者 " ' " 或者 ' " ' 或者 ''' " ' '''
字符串的序号:正向递增序列以及反向递减序列
字符串的索引:返回字符串中的单个字符 <字符串>[M]
字符串的切片:返回字符串中的多个字符 <字符串> [M:N]
字符串中的转义符:\表示文本中的特定字符的含义,当作特定文本的解释
"\b"回退 "\n"换行(光标回到文本的下一行) "\r"回车(光标回到文本的首行)
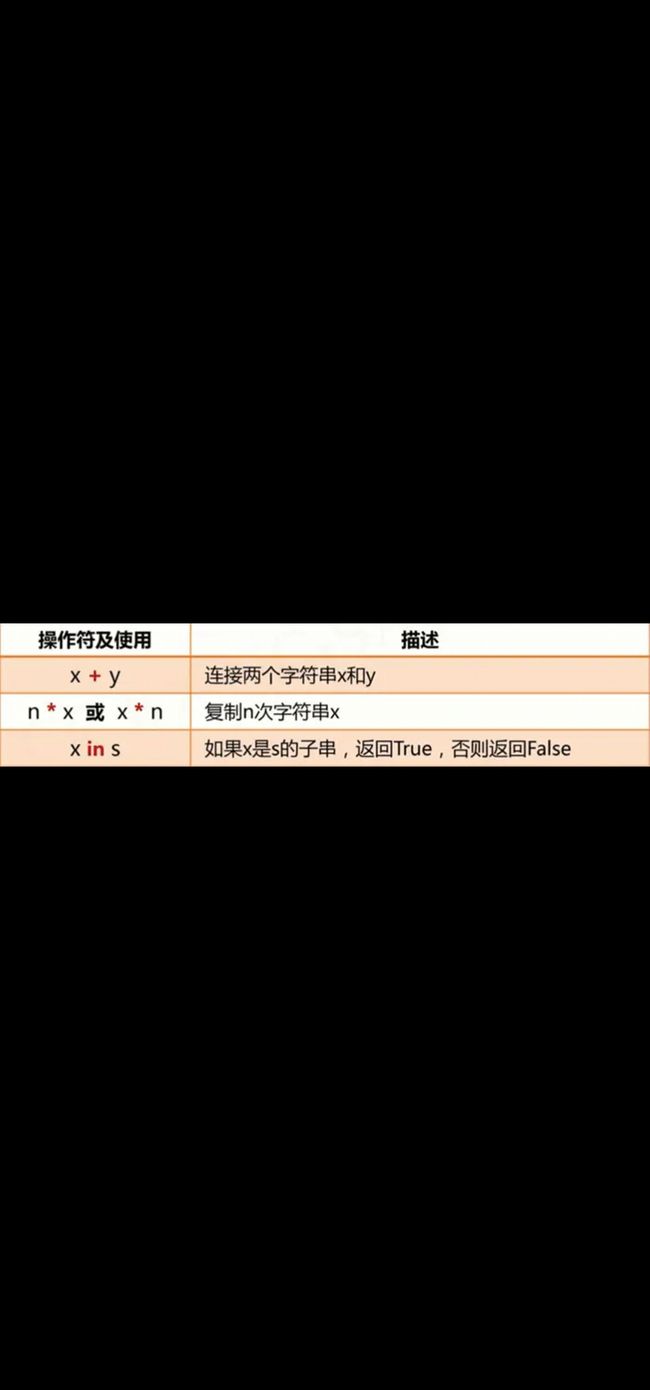
3.3.2 字符串操作符
获取星期字符串:
#WeekNamePrintV1.py
weekStr="星期一星期二星期三星期四星期五星期六星期日"
weekId=eval(input("请输入星期数字(1-7):"))
pos=(weekId-1)*3
print(weekStr[pos:pos+3])
简便操作:
#WeekNamePrintV1.py
weekStr="一二三四五六七"
weekId=eval(input("请输入星期数字(1-7):"))
print("星期"+weekStr[weekId-1])
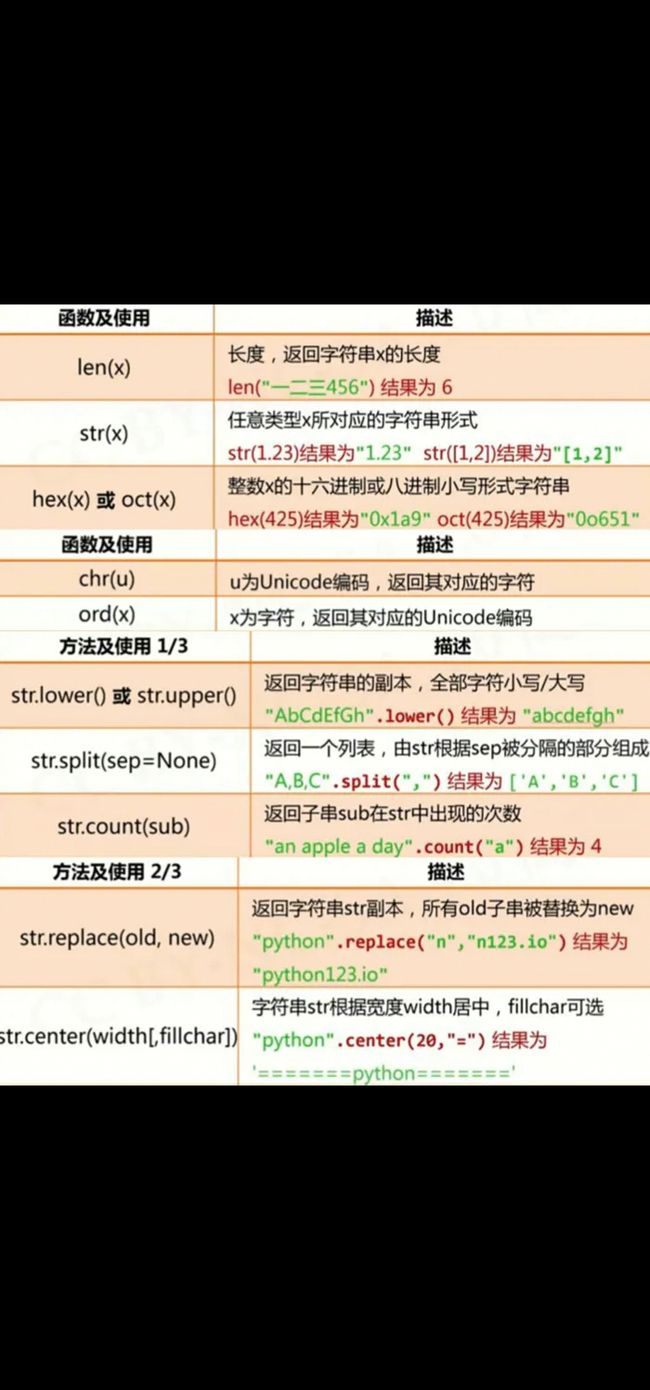
3.3.3 字符串处理函数
3.3.4 字符串处理方法
定义:方法为一种专有名词
形式:.() 与a有关
八个字符串处理方法
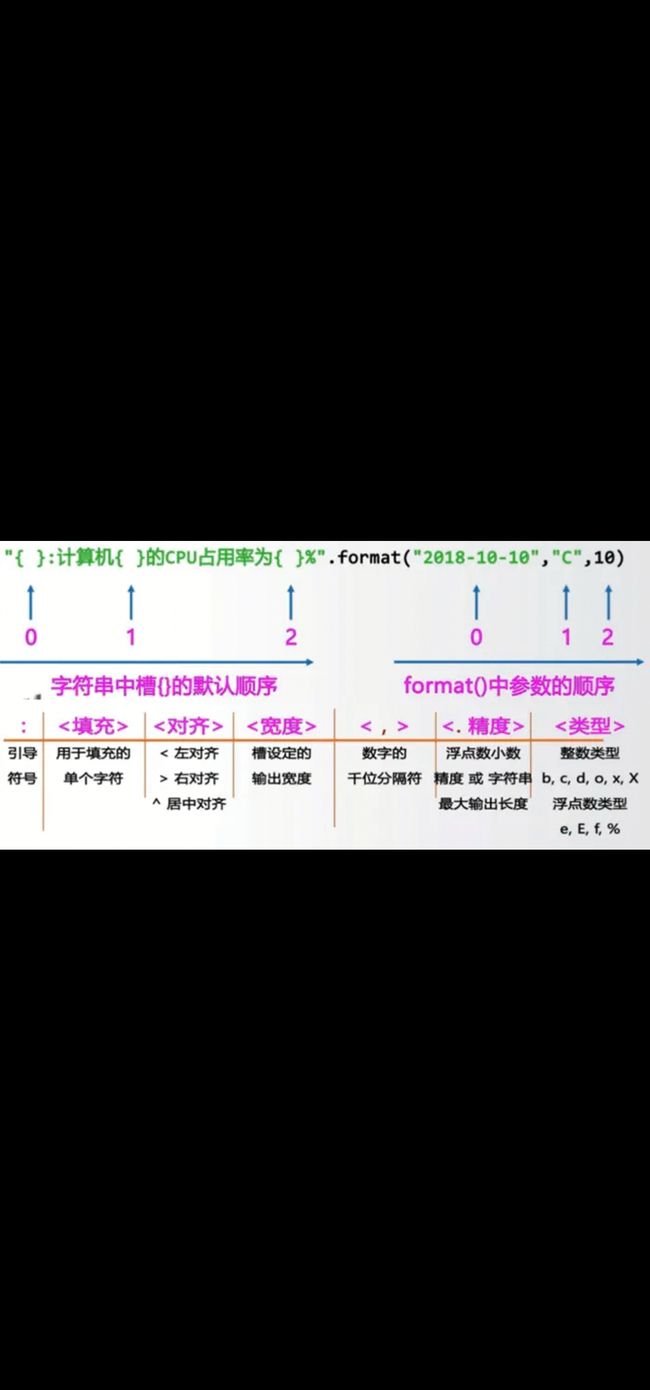
字符串的格式化:.format()
表示:<模板字符串>.format(<逗号分隔符的参数>)
槽:"{}=
填充,对齐,宽度
"{0:=^20}".format("PYTHON")
"{0:*>20}".format("BIT")
分隔符,精度,类型
"{0:b},{0:c},{0:d},{0:o},{0:x},{0;X}".format(425)
"{0:e},{0:f},{0:E},{0:%}".format(3.14)
3.4 time库的使用
3.4.1 time库基本介绍
定义:time库是处理时间的标准库,可以获取系统时间并且格式化输出
用途:提供系统计时功能,用于系统性能分析
用途:提供系统计时功能,用于系统性能分析
表示:import time time.()
包含:时间获取、时间格式化、程序计时
3.4.2 时间获取
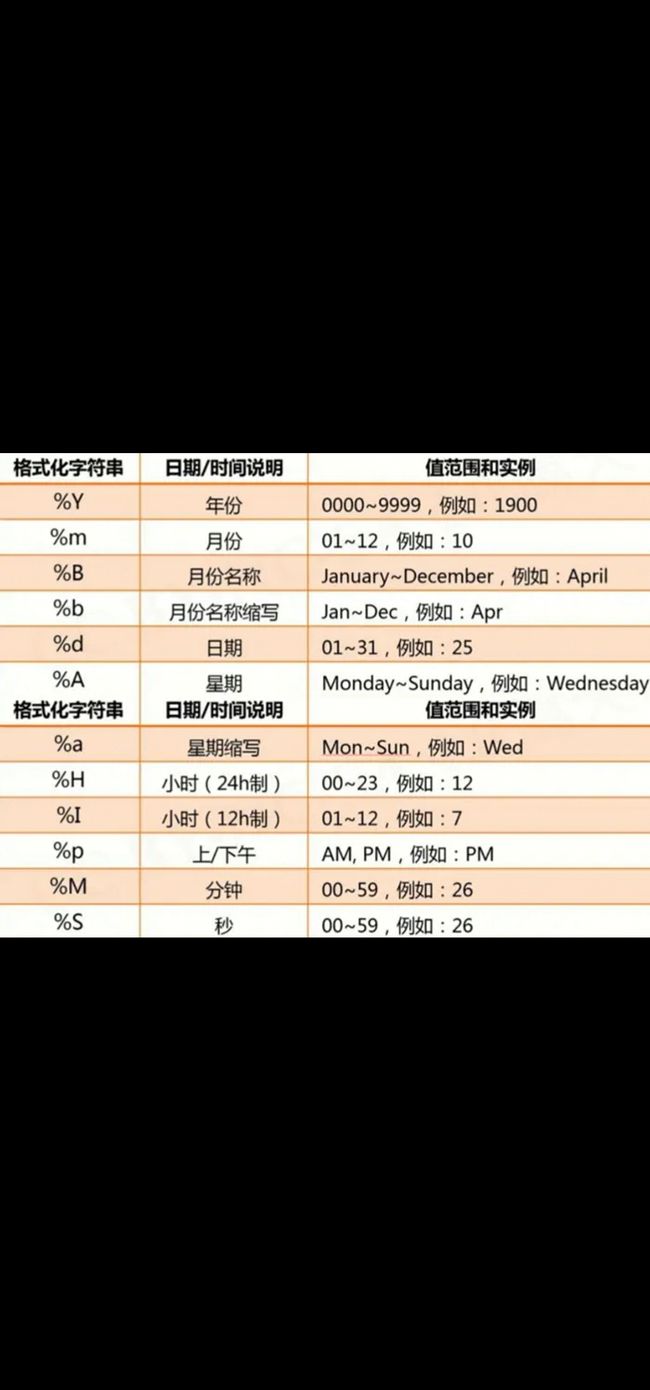
3.4.3 时间格式化
定义:将时间以合理的方式展现出来,类似字符串格式化,需要有展示模板
实现方法:strftime() 函数
strftime(tpl,ts)
#获取时间
t=time.gmtime()
time.strftime("%Y-%m-%d %H:%M:%S,t")
strptime与之相反
#逆向获取时间
timeStr="2019-01-29 14:41:55"
time.strptime(timeStr,"%Y-%m-%d %H:%M:%S")
3.4.4 程序计时应用
定义:起止经历的时间过程
分类:测量时间、产生时间
测量时间:perf_counter() 连续调用计算差值
产生时间:sleep() 让程序休眠
#连续调用计算差值
start=time.perf_counter()
end=time.perf_counter()
end-start
#休眠
def wait()
time.sleep(3.3)
wait()
3.5 文本进度条
3.5.1 简单进度条
文本进度条:采用字符串方式打印可以动态变化的文本进度条,需要在一行中逐渐变化
#TextProBar.V1.py
import time
scale=10
print("-----执行开始-----")
for i in range(scale+1):
a='*'*i
b='.'*(scale-i)
c=(i/scale)*100
print("{:^3.0f}%[{}->{}]".format(c,a,b))
time.sleep(0.1)
print("-----执行结束-----")
3.5.2 单行动态刷新
方法:用打印后的字符覆盖之前的字符,打印后光标需要回到原位置(/r)
#TextProBar.V2.py
import time
for i in range(101):
print("/r{:3}%".format(i),end='')
time.sleep(0.1)
3.5.3 文本刷新完整实例
#TextProBar.V3.py
import time
scale=50
print("执行开始".center(scale//2,"-"))
start=time.perf_counter()
for i in range(scale+1):
a='*'*i
b='.'*(scale-i)
c=(i/scale)*100
dur=time.perf_counter()-start
print("/r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,dur),end='')
time.sleep(0.1)
print("/n"+"执行结束".center(scale//2),'_')
一些其他进度条函数