Python宽搜(BFS)和深搜(DFS)
目录
- BFS
-
- BFS是什么
- BPS工作过程和原理
- BFS应用场景
- python实现BFS(树和图)
-
- python实现BFS图
- python实现图的最短路径
- python实现BFS树
- DFS
-
- DFS是什么
- DFS工作过程和原理
- DFS应用场景
- python实现DFS
-
- python实现DFS图
- python实现DFS树
- 何时使用深搜和广搜
- python实现树前中后序遍历
-
- 前序遍历
- 中序遍历
- 后序遍历
- 参考资料
BFS
BFS是什么
BFS称为宽度优先搜索也叫做广度优先搜索,其别名又叫BFS,属于一种盲目搜寻法。
Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
目的是系统地展开并检查图中的所有节点,以找寻结果。
换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,故得名。
广度优先搜索使用队列(queue)来实现,队列(queue)有着先进先出FIFO(First Input First Output)的特性。
BPS工作过程和原理
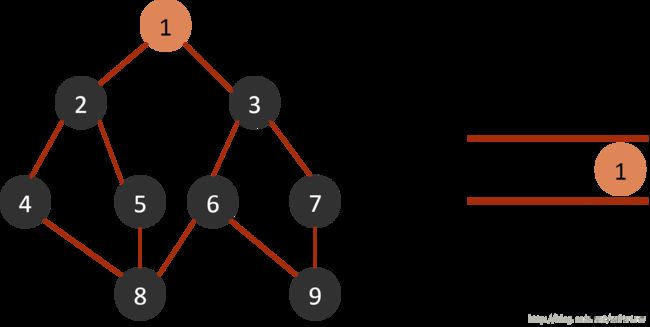
BFS操作步骤如下:
1、把起始点放入queue;
2、重复下述2步骤,直到queue为空为止:
1)从queue中取出队列队首;
2)找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
(2)从queue中取出队列头的节点1,找出与节点1邻接的节点2,3,标记为已遍历,然后放入queue中。

(3)从queue中取出队列头的节点2,找出与节点2邻接的节点1,4,5,由于节点1已遍历,排除;标记4,5为已遍历,然后放入queue中。

(4)从queue中取出队列头的节点3,找出与节点3邻接的节点1,6,7,由于节点1已遍历,排除;标记6,7为已遍历,然后放入queue中。
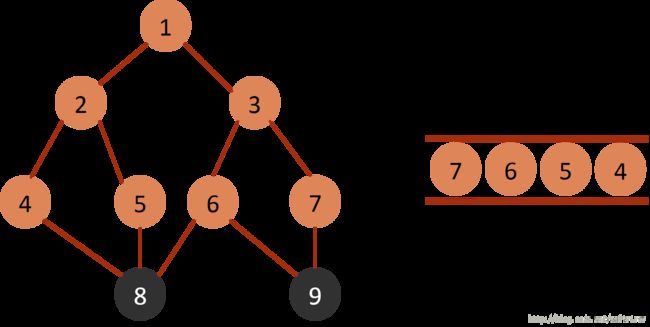
(5)从queue中取出队列头的节点4,找出与节点4邻接的节点2,8,2属于已遍历点,排除;因此标记节点8为已遍历,然后放入queue中。
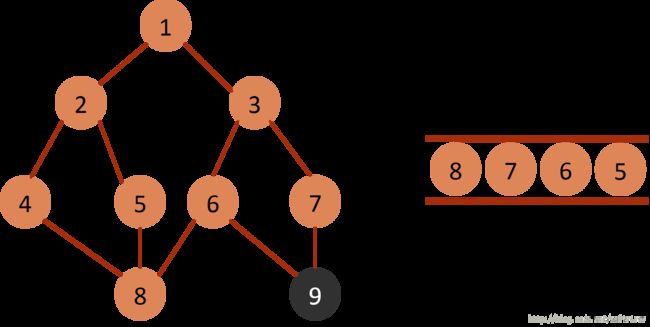
(6)从queue中取出队列头的节点5,找出与节点5邻接的节点2,8,2,8均属于已遍历点,不作下一步操作。

(7)从queue中取出队列头的节点6,找出与节点6邻接的节点3,8,9,3,8属于已遍历点,排除;因此标记节点9为已遍历,然后放入queue中。
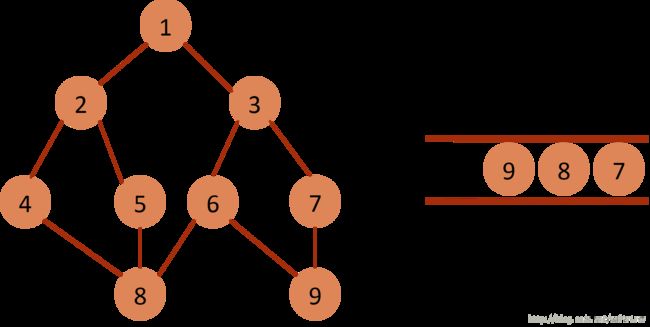
(8)从queue中取出队列头的节点7,找出与节点7邻接的节点3, 9,3,9属于已遍历点,不作下一步操作。

(9)从queue中取出队列头的节点8,找出与节点8邻接的节点4,5,6,4,5,6属于已遍历点,不作下一步操作。
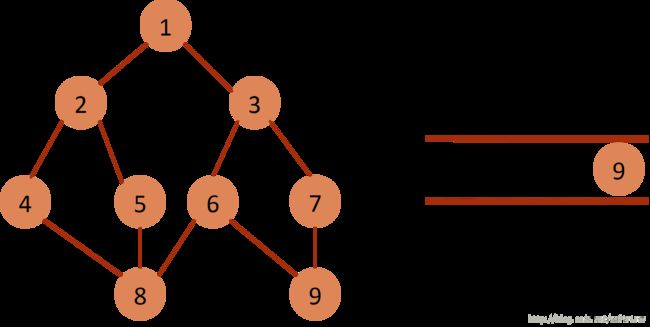
(10)从queue中取出队列头的节点9,找出与节点9邻接的节点6,7,6,7属于已遍历点,不作下一步操作。
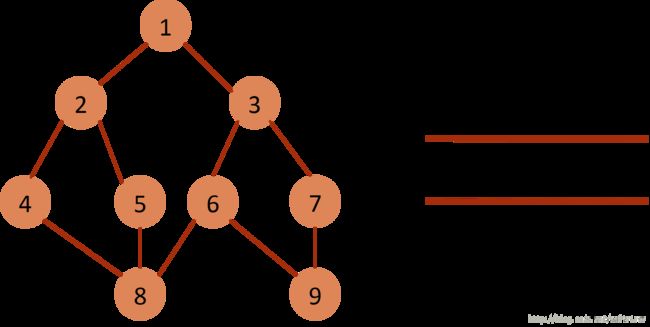
(11)queue为空,BFS遍历结束。
BFS应用场景
- BFS的两个场景:层序遍历、最短路径
- 找距离某一点的最短路,但路径不唯一,最先搜索到满足条件的就是最短的路径
- 大范围的查找
- 出现 “最短”、“最少”类似字眼的可以优先考虑
python实现BFS(树和图)
树是特殊的图
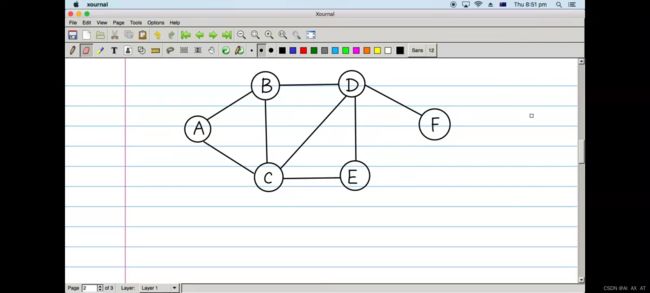
python实现BFS图
import os
import sys
'''
python实现BFS的图
2022-01-15
'''
# 创建一个字典,用于存储图。字典相当于映射关系,通过键值对进行读取。适用于图只有少量的点,数据过多使用python类更为合适
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# 开始BFS遍历
# graph是图数据,s是图的起点
def BFS(graph, s):
# 创建一个数组作为队列,用于存储未访问过的点
queue = []
# 放入起点
queue.append(s)
# 创建一个集合,用于存放已读入的点,例如起点s
seen = set()
seen.add(s)
# 循环读queue
while (len(queue) > 0):
# 通过queue.pop(0)读取队列队首,即每个点
vertex = queue.pop(0)
# 读取每个点相邻的点
nodes = graph[vertex]
# 判重:循环判断相邻的点是否读过
for w in nodes:
if w not in seen:
queue.append(w)
seen.add(w)
# 输出遍历节点
print(vertex, end= ' ')
BFS(graph, "A")
'''
# 运行结果
A B C D E F
'''
python实现图的最短路径
import os
import sys
'''
python实现BFS的图
2022-01-15
'''
# 创建一个字典,用于存储图。字典相当于映射关系,通过键值对进行读取。适用于图只有少量的点,数据过多使用python类更为合适
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# 开始BFS遍历
# graph是图数据,s是图的起点
def BFS(graph, s):
# 创建一个数组作为队列,用于存储未访问过的点
queue = []
# 放入起点
queue.append(s)
# 创建一个集合,用于存放已读入的点,例如起点s
seen = set()
seen.add(s)
# 路径还原,把访问的点和它前一个点对应起来,形成一个键值对,利用它来完成最短路径的输出
parent = {s: None}
# 循环读queue
while (len(queue) > 0):
# 通过queue.pop(0)读取队列队首,即每个点
vertex = queue.pop(0)
# 读取每个点相邻的点
nodes = graph[vertex]
# 判重:循环判断相邻的点是否读过
for w in nodes:
if w not in seen:
queue.append(w)
seen.add(w)
parent[w] = vertex
# 输出遍历节点
# print(vertex, end= ' ')
return parent
parent = BFS(graph, "A")
# 输出你想要的到最短路径
# 设v为终点
v = 'F'
# 循环查找v
while v != None:
print(v, end=' ')
v = parent[v]
'''
# 运行结果
F D B A
'''
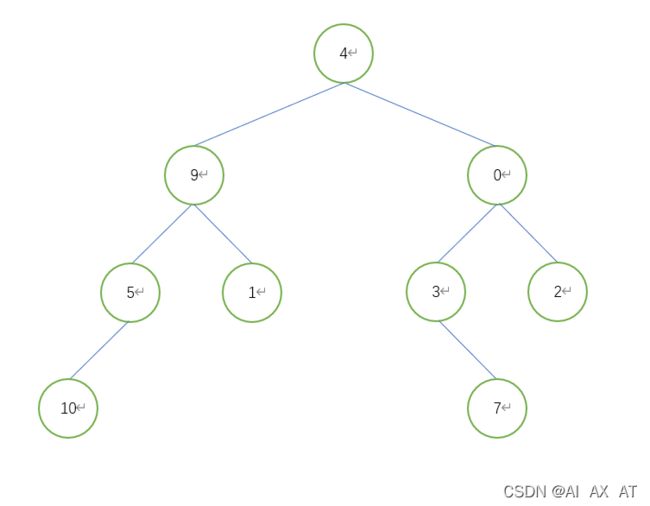
python实现BFS树
# 定义一个树的节点
class TreeNode:
def __init__(self, x):
self.val = x # 值
self.left = None # 左节点
self.right = None # 右节点
def level_order_tree(root):
if not root: # 一个树只有根节点,返回空值
return root
queue = []
result = []
queue.append(root) # 将根节点入队
result.append(root.val) # 添加根节点值
while len(queue) > 0:
node = queue.pop(0) # 取队列队首
result.append(node.val)
# 判断左右子树
if node.left: # 添加左子树的孩子到队列
queue.append(node.left)
if node.right: # 添加右子树的孩子到队列
queue.append(node.right)
return result
if __name__ == "__main__":
tree = TreeNode(4)
tree.left = TreeNode(9)
tree.right = TreeNode(0)
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
print(level_order_tree(tree))
# [4, 9, 0, 5, 1, 3, 2, 10, 7]
DFS
DFS是什么
- 深度优先搜索算法(英语:Depth-First-Search,简称DFS)是一种用于遍历或搜索树或图的算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
- 当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。
- 对于同一颗的树或图,其DFS序不一定唯一。
- 深度优先搜索使用栈(stack)来实现,栈(stack)有着先进后出的特性。
DFS工作过程和原理
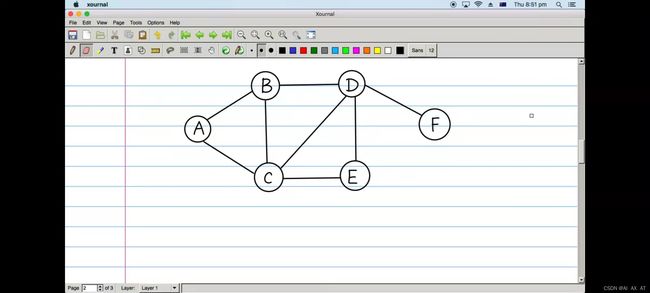
- 以A为开始节点,访问A,与A相连的邻接点有B和C。
- 此时可以访问B和C,访问哪个取决于你压栈的顺序。
- 访问B,与B相连的邻接点有C和D。
- 访问D,与D相连的邻接点有E和F。
- 访问F,F没有邻接点,原路返回来时最近的邻接点D。
- 与D相连的邻接点E没被访问过,访问E,与E相连的邻接点有C和D。
- 访问C,C的邻接点有A、B、D和E,全被访问过了,原路返回D,此时D的邻接点都被访问过了,原路返回B,再到A。
DFS应用场景
- 求子序列、求子集
- 找所有可能的解决方案,逐层组装结果(跟第一种没太大差别)
python实现DFS
python实现DFS图
import os
import sys
'''
python实现DFS的图
2022-01-15
'''
# 创建一个字典,用于存储图。字典相当于映射关系,通过键值对进行读取。适用于图只有少量的点,数据过多使用python类更为合适
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
# 开始DFS遍历
# graph是图数据,s是图的起点
def BFS(graph, s):
# 创建一个数组作为栈,用于存储未访问过的点
stack = []
# 放入起点
stack.append(s)
# 创建一个集合,用于存放已读入的点,例如起点s
seen = set()
seen.add(s)
# 循环读stack
while (len(stack) > 0):
# 通过queue.pop()读取栈最后一个
vertex = stack.pop()
# 读取每个点相邻的点
nodes = graph[vertex]
# 判重:循环判断相邻的点是否读过
for w in nodes:
if w not in seen:
stack.append(w)
seen.add(w)
# 输出遍历节点
print(vertex, end= ' ')
BFS(graph, "A")
'''
# 运行结果
A C E D F B
'''
python实现DFS树
# 创建树节点类val:值,left:左子树,right:右子树
class TreeNode:
def __init__(self, value):
self.val = value
self.left = None
self.right = None
# 深搜遍历二叉树
def DFS(root):
# 创建存放结果数组
res = []
# 创建栈,栈具有后进先出的特性,首先放入根节点
stack = [root]
# 循环栈
while stack:
# 取出栈最后一个元素
currentNode = stack.pop()
# 田间取出元素的值
res.append(currentNode.val)
# 是否含右子树
if currentNode.right:
# 添加右子树到栈
stack.append(currentNode.right)
# 是否含左子树
if currentNode.left:
# 添加左子树到栈
stack.append(currentNode.left)
# 返回结果
return res
if __name__ == "__main__":
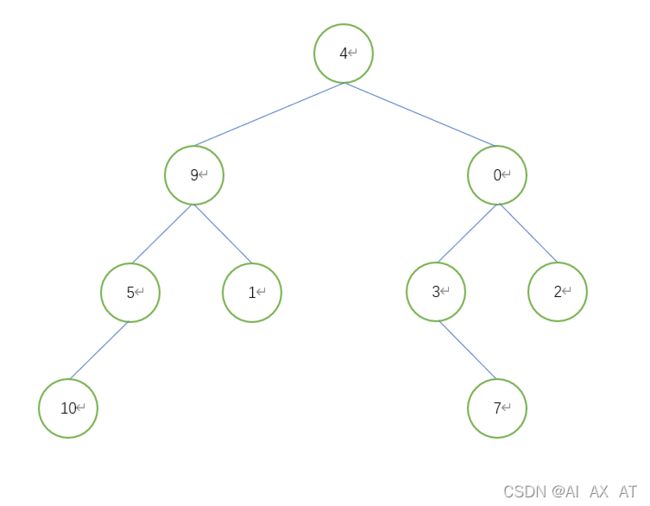
tree = TreeNode(4) # 添加根节点
tree.left = TreeNode(9) # 添加根左子树
tree.right = TreeNode(0) # 添加根右子树,以下以此类推
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(DFS(tree))
# [4, 9, 5, 10, 1, 0, 3, 7, 2]
'''
运行结果:
[4, 9, 5, 10, 1, 0, 3, 7, 2]
'''
何时使用深搜和广搜
- BFS是用来搜索最短径路的解是比较合适的,比如求最少步数的解,最少交换次数的解,因为BFS搜索过程中遇到的解一定是离根最近的,所以遇到一个解,一定就是最优解,此时搜索算法可以终止。这个时候不适宜使用DFS,因为DFS搜索到的解不一定是离根最近的,只有全局搜索完毕,才能从所有解中找出离根的最近的解。(当然这个DFS的不足,可以使用迭代加深搜索ID-DFS去弥补)。
- 空间优劣上,DFS是有优势的,DFS不需要保存搜索过程中的状态,而BFS在搜索过程中需要保存搜索过的状态,而且一般情况需要一个队列来记录。
- DFS适合搜索全部的解,因为要搜索全部的解,那么BFS搜索过程中,遇到离根最近的解,并没有什么用,也必须遍历完整棵搜索树,DFS搜索也会搜索全部,但是相比DFS不用记录过多信息,所以搜素全部解的问题,DFS显然更加合适。
python实现树前中后序遍历
前序遍历
# 定义一个树的节点
class TreeNode:
def __init__(self, x):
self.val = x # 值
self.left = None # 左节点
self.right = None # 右节点
# 前序遍历,lis是传入的list型参数,为了递归得到一个遍历List结果
def preorder(root, result):
result.append(root.val) # 添加根节点值
if root.left:
preorder(root.left, result) # 递归寻找左子树
if root.right:
preorder(root.right, result) # 递归寻找右子树
return result
if __name__ == "__main__":
tree = TreeNode(4) # 添加根节点
tree.left = TreeNode(9) # 添加根左子树
tree.right = TreeNode(0) # 添加根右子树,以下以此类推
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(preorder(tree, []))
# [4, 9, 5, 10, 1, 0, 3, 7, 2]
中序遍历
# 定义一个树的节点
class TreeNode:
def __init__(self, x):
self.val = x # 值
self.left = None # 左节点
self.right = None # 右节点
# 中序遍历,lis是传入的list型参数,为了递归得到一个遍历List结果
def infix_order(root, result):
if root.left:
infix_order(root.left, result)
result.append(root.val)
if root.right:
infix_order(root.right, result)
return result
if __name__ == "__main__":
tree = TreeNode(4) # 添加根节点
tree.left = TreeNode(9) # 添加根左子树
tree.right = TreeNode(0) # 添加根右子树,以下以此类推
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(infix_order(tree, []))
# [10, 5, 9, 1, 4, 3, 7, 0, 2]
后序遍历
# 定义一个树的节点
class TreeNode:
def __init__(self, x):
self.val = x # 值
self.left = None # 左节点
self.right = None # 右节点
# 后序遍历,result是传入的list型参数,为了递归得到一个遍历List结果
def epilogue(root, result):
if root.left:
epilogue(root.left, result)
if root.right:
epilogue(root.right, result)
result.append(root.val)
return result
if __name__ == "__main__":
tree = TreeNode(4) # 添加根节点
tree.left = TreeNode(9) # 添加根左子树
tree.right = TreeNode(0) # 添加根右子树,以下以此类推
tree.left.left = TreeNode(5)
tree.left.right = TreeNode(1)
tree.right.left = TreeNode(3)
tree.right.right = TreeNode(2)
tree.left.left.left = TreeNode(10)
tree.right.left.right = TreeNode(7)
print(epilogue(tree, []))
# [10, 5, 1, 9, 7, 3, 2, 0, 4]
参考资料
- 图论(四)宽度优先搜索BFS
- 树的前序、中序、后序遍历及深度优先算法DFS、广度优先算法BFS及python实现
- 什么使用用广度搜索(bfs)什么时候用深度搜索(dfs)?