1. PWA(Progressive Web App)
PWA的离线体验,在断网情况下DNS查询都会失败,为什么还能正常展示页面呢?
PWA 会指向一个清单 (manifest) 文件,其中包含网站相关的信息,包括图标,背景屏幕,颜色和默认方向。(在第5章中,你将学习到如何使用清单文件来使你的网站更加吸引人)
PWA 还可以离线工作。使用 Service Workers,你可以选择性地缓存部分网站以提供离线体验。
由于 PWA 只是汲取了丰富功能的网站,因此可以通过搜索引擎轻松发现。人们可以很自然地通过社交媒体链接或浏览网页发现 PWA。构建 PWA 可以让你接触比单独使用原生应用更多的人,因为它们是为任何能够运行浏览器的平台而构建的!
PWA特点:
- 响应式的 - 它适应较小的屏幕尺寸
- 连接无关 - 由于 Service Worker 缓存,它可以离线工作
- 应用式的交互 - 它使用应用外壳架构进行构建
- 始终保持最新 - 感谢 Service Worker 的更新过程
- 安全的 - 它通过 HTTPS 进行工作
- 可发现的 - 搜索引擎可以找到它
- 可安装的 - 使用清单文件
- 可链接的 - 可以简单的通过 URL 来共享
1.2 Service Workers: PWA 的关键
释放 PWA 力量的关键在于 Service Workers 。就其核心来说,Service Workers 只是后台运行的 worker 脚本。它们是用 JavaScript 编写的,只需短短几行代码,它们便可使开发者能够拦截网络请求,处理推送消息并执行许多其他任务。
最棒的一点是,如果用户的浏览器不支持 Service Workers 的话,它们只是简单地回退,你的网站还作为普通的网站。正是由于这一点,它们被描述为“完美的渐进增强”。渐进增强术语是指你可以先创建能在任何地方运行的体验,然后为支持更高级功能的设备增强体验。
虽然 Service Workers 是用 JavaScript 编写的,但需要明白它们与你的标准 JavaScript 文件略有不同,这一点很重要。Service Worker:
- 运行在它自己的全局脚本上下文中
- 不绑定到具体的网页
- 无法修改网页中的元素,因为它无法访问 DOM
-
只能使用 HTTPS
Service Worker 运行在 worker 上下文中,这意味着它无法访问 DOM,它与应用的主要 JavaScript 运行在不同的线程上,所以它不会被阻塞。它们被设计成是完全异步的,因此你无法使用诸如同步 XHR 和 localStorage 之类的功能。在上面的图1.3中,你可以看到 Service Worker 处于不同的线程,并且可以拦截网络请求。记住,Service Worker 就像是“空中交通管制员”,它可以让你全权控制网站中所有进出的网络请求。这种能力使它们极其强大,并允许你来决定如何响应请求。
当用户首次导航至 URL 时,服务器会返回响应的网页。在图1.4中,你可以看到在第1步中,当你调用 register() 函数时, Service Worker 开始下载。在注册过程中,浏览器会下载、解析并执行 Service Worker (第2步)。如果在此步骤中出现任何错误,register() 返回的 promise 都会执行 reject 操作,并且 Service Worker 会被废弃。
一旦 Service Worker 成功执行了,install 事件就会激活 (第3步)。Service Workers 很棒的一点就是它们是基于事件的,这意味着你可以进入这些事件中的任意一个。我们将在本书的第3章中使用这些不同的事件来实现超快速缓存技术。
一旦安装这步完成,Service Worker 便会激活 (第4步) 并控制在其范围内的一切。如果生命周期中的所有事件都成功了,Service Worker 便已准备就绪,随时可以使用了!
2.2.1 应用外壳架构
\就个人而言,我觉得 Facebook 的原生应用为用户提供了非常棒的体验。当你离线时它会给你提示,它会缓存你的时间轴,以便你能更快地访问,它还能做到瞬间加载。如果你有一段时间没有访问 Facebook 的原生应用,你仍会在任何动态内容加载之前,立即看到一个空的“UI 外壳”,包括头部和导航条。
使用智能的 Service Worker 缓存,你实际上可以缓存你网站的 UI 外壳,以便用户重复访问。这些新功能使我们能够以不同的方式来思考和构建网站。
此刻你可能想知道什么是 “UI 外壳”:它只是用户界面所必需的最小化的 HTML、CSS 和 JavaScript 。它可能会是类似网站头部,底部和导航这样没有任何动态内容的部分。如果我们能加载并缓存 UI 外壳,我们就可以在稍后的阶段将动态内容加载到页面中。Google 的 Inbox 就是一个很好的现成例子:
2. DNS多级缓存
DNS的整体结构
是不是很像CDN的架构?我们把DNS分布式存储服务器看作CDN源站,把DNS查询的缓存服务器看作是就近的CDN边缘站点,简直就是相同的架构。理解了这一点,非常有益于在整体上把我DNS的精髓,即它对查询效率的要求非常高,同时它的应用又非常普遍,这就要求查询既要是分布式的,又要是快速的。
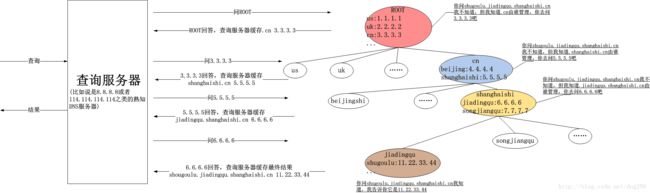
DNS的查询过程
请注意那些叫做查询服务器的节点,它们试图在本机保存整个分布式的管理结构的信息,这就是所谓的多级缓存!也就是说,它们并不一定非要保存域名和IP地址的直接对应信息,如果没有找到这个对应,它们会努力帮你找到离目标最近的管理服务器,比如虽然它没有shugoulu.jiadingqu.shanghaishi.cn.,但是它有shanghaishi.cn.,这也算是一种命中,至少查询不会从根部开始了。
这意味着什么?
这种设计无形中大幅降低了根管理服务器的流量压力,只有在查询服务器把各级缓存全都遗忘的时候,才会从根部开始一次查询,而这次新的查询结束后,查询服务器又会把它记住,直到岁月导致的遗忘。
如果同一个查询服务器收到了一个同样的DNS解析请求,它将按照下面的流程行事:
再看上面这个结构,由于是分布式的授权管理结构,如果哪个域名的IP地址变化了,不像集中式的hosts文件那般牵一发而动全身了,直接把更改过的信息上报给你的授权方即可,到此为止这次的变更通知就结束了,你的授权方不必把你的域名IP地址的变更信息再通知更上面的授权方,这就是授权模型的好处,它正是这句中世纪古话“我的领主的领主不是我的领主,我的附庸的附庸不是我的附庸”的完美体现!
3. 算法&智力题 给一串无序的数字,找出中位数。在put一位,继续找,继续put,继续找。时间复杂度为O(log2n)。用堆实现。
思路1) 把无序数组排好序,取出中间的元素
时间复杂度 采用普通的比较排序法 O(N*logN)
如果采用非比较的计数排序等方法, 时间复杂度 O(N), 空间复杂度也是O(N).
思路2)
2.1)将前(n+1)/2个元素调整为一个小顶堆,
2.2)对后续的每一个元素,和堆顶比较,如果小于等于堆顶,丢弃之,取下一个元素。 如果大于堆顶,用该元素取代堆顶,调整堆,取下一元素。重复2.2步
2.3) 当遍历完所有元素之后,堆顶即是中位数。
首先将数组的前(n+1)/2个元素建立一个最小堆。
然后,对于下一个元素,和堆顶的元素比较,如果小于等于,丢弃之,接着看下一个元素。如果大于,则用该元素取代堆顶,再调整堆,接着看下一个元素。重复这个步骤,直到数组为空。
当数组都遍历完了,那么,堆顶的元素即是中位数。
可以看出,长度为(n+1)/2的最小堆是解决方案的精华之处。
public static double median(int[] array){
int heapSize = array.length/2 + 1;
PriorityQueue heap = new PriorityQueue<>(heapSize);
for(int i=0; i 思路3) 熟话说,想让算法跑的更快,用分治!
快速排序之所以得名"快排",绝非浪得虚名!因为快排就是一种分治排序法!
同样,找中位数也可以用快排分治的思想。具体如下:
任意挑一个元素,以改元素为支点,划分集合为两部分,如果左侧集合长度恰为 (n-1)/2,那么支点恰为中位数。如果左侧长度<(n-1)/2, 那么中位点在右侧,反之,中位数在左侧。 进入相应的一侧继续寻找中位点。
这种方法很快,但是在最坏的情况下时间复杂度为O(N^2), 不过平均时间复杂度好像是O(N)。
public static double median2(int[] array){
if(array==null || array.length==0) return 0;
int left = 0;
int right = array.length-1;
int midIndex = right >> 1;
int index = -1;
while(index != midIndex){
index = partition(array, left, right);
if(index < midIndex) left = index + 1;
else if (index > midIndex) right = index - 1;
else break;
}
return array[index];
}
public static int partition(int[] array, int left, int right){
if(left > right) return -1;
int pos = right;
right--;
while(left <= right){
while(leftleft && array[right]>array[pos]) right--;
if(left >= right) break;
swap(array, left, right);
}
swap(array, left, pos);
return left;
}
2.智力题,三个箱子里面各有两格,有的放了金块,有的放了银块,两次都抽到金块的概率(大致这样,原题记不清了)
3.同样智力题,n*2的方格,M种颜色,每个相邻格子不能涂相同颜色,有多少种涂法
2.一个明星,n个其他人,其他人互不认识,但是认识明星,明星不认识其他人,s(A,B) == true 表示A认识B,s(A,B) == false表示A不认识B,O(N)找出明星。
一种思路:取出两个人,如1号和2号,如果1号认识2号,那么1号不是明星,去除1号;如果1号不认识2号,那么2号不是明星,去除2号。如此比下去,遍历一遍,即可找出明星(剩下的那个)。时间复杂度O(n)。
bool isRecgn(int i,int j); //判断i是否认识j
//n个人中找明星 n>1
int find(int a[],int n)
{
int i=0,j=1;
int cand = i;
while(jn)
break;
}
else{
cand = i;
if(++j>n)
break;
}
}
return cand;
}
用两个指针i和j分别指向前、后的两个人,比较一次根据比较结果做一次位置调整。
1. 逻辑题 四张卡片 卡片正面是数字,反面是字母
现在桌上四张卡片 状态 a 1 b 2
现在我想要证明 a的反面必然是1 我只能翻两张牌,我翻哪两张?
a和2
2.五队夫妇参加聚会,每个人不能和自己的配偶握手,只能最多和他人握手一次。A问了其他人,发现每个人的握手次数都不同,那么A的配偶握手了几次?
显然 ,每个人不会和自己握手 ,也不会和自己的配偶握手 .当然某两人之间也不会握两次手 .此外 ,由于各种原因造成可握手的人并不一定都握手 .因此在他们这 10个人中 ,握手次数最多的人握手的次数也不能大于 8.而王先生已经问得九个人握手的次数都不相同 .所以他们握手的次数应该分别是 0 ,1,2 ,3 ,4,5 ,6,7,8,共九种情形 .分析可得 :握手次数为 8的人和握手次数为零的人必定是一对夫妻 .这是因为握手次数为 8的人 ,不妨假定为张先生 ,他必和除张太太以外的四对夫妇中的每个人都握了手 .于是这四对夫妇中的每个人握手的次数都不能是零 .那么 ,握手次数为零者只能是张太太了 .这样 ,张氏夫妇的握手次数已经确定 ,予以排除...。而握手7次的人,和除了自己太太、张太太以外的人都握了手,那么握了手的人的握手次数都会大于1,所以只有自己太太的握手次数能为1。那么既然握手次数之和为8的必定是一对夫妻,九人中又没有两个人握手的次数相同,所以只有王先生和王太太握手次数同为4次
3.运用面向对象思想,设计一个有 歌手 歌曲 专辑 搜索功能的音乐app
4.智力题,你只能带行走60公里的油,只能在起始点加油,如何穿过80公里的沙漠?
1)首先我们可以假设走1公里需要1升油。那么卡车的载油能力为60升。
2)因为卡车的总载油能力为60升,卡车每公里耗油1升,为了消耗最少的汽油,最后一个储油点应该离终点60公里,且此处中储油60升,这样恰好能穿越沙漠.即储油点m=1处离终点60公里, 即离起点20公里,储油60升;
3)为了在m=1处储60升汽油,卡车先在起点装满60升油,行驶至m=1处,此时剩余40升。放20升在m=1处,剩余20升,然后再回到起点,剩余0升。
4)在起点再加满60升,行驶至m=1处,消耗20升,而之前在m=1处存储了20升,加上,此时刚好剩余60升,离终点60公里,done。
起点总耗油量为60+60=120。
扩展:81公里呢?
第一次最多可以在m=1处放60-21-21=18升,回到。最后一次,正式启程到m=1处剩余39升。那么60-18-39=3,即第二次应在m=1处存储3升,3+21+21=45,即第二次应加入45升。总的就是60+45+60=165升。
1.求正,负数组其中的两元素之和最接近零的这两元素,并说出你这种解法的时间复杂度
2.链表,栈,队列相关问题
3.赛马问题,25匹马,5个赛道,最少几次能选出最快的三匹马?
正确答案: 7 场。
推理过程:你可以先询问面试官,「最快」的意思,是不是指比赛时总能赢?在真实情况下并非如此。但倘若你假设, A 在比赛中跑赢了 B , A 就无可争议地跑得更快,这就极大地简化了这道谜题。
面试官会告诉你,这么想没有问题,比赛就是为了选出跑得最快的马。
通常,你会下意识地想,至少需要 5 场比赛。任何一匹马都可能排名前三,所以,你必须让所有的 25 匹马都参加比赛。可每次只让 5 匹马参赛,少于 5 场比赛没法让所有的马都参赛。
很好。接下来你的结论会是:只有 5 场比赛还不够。第一轮,把 25 匹马分为 5 组,每组里的马只跑一次,只跟同组的马匹竞争。
一轮比赛结果大概会是这样:
- 第一名:「奔腾」
- 第二名:「北舞」
- 第三名:「凯速」
- 第四名:「上将」
- 第五名:「跳影」
你无法断定「奔腾」是 25 匹马里跑得最快的,甚至无法担保它能排进前三名。举个极端情况下的相反例子:其他 4 场比赛中跑得最慢的马,也可能比「奔腾」跑得快,因为它的速度可能在 25 匹马里排第 21 名。
那么,从这场比赛里我们是否了解到什么东西呢?当然了。我们了解到这 5 匹马的排名情况。我们还了解到,「上将」和「跳影」可以排除在外了。既然它们在这一轮比赛里排不进前三,那么在所有的 25 匹马里,它们同样不可能排进前三。。这个道理,也适用于其他轮比赛里的第 4 名和第 5 名。每一轮比赛可以排除掉两匹马。在第一轮的 5 场比赛中,我们可以刷掉 10 匹马,留下 15 匹马竞争前三名。
第二轮,即第 6 场比赛,要测试在最初 5 场比赛中表现出色者。合理的方案是让 5 匹上一轮比赛的「第一名」对战。就这么做吧!让「奔腾」和其他 4 场比赛的第一名跑一回。结果可能会是这样:
- 第一名:「易歌尔」
- 第二名:「奔腾」
- 第三名:「终结者」
- 第四名:「红朗姆」
- 第五名:「菲尔拉普」
这一次,我们又可以排除两匹马,「红朗姆」和「菲尔拉普」。从这一次的比赛结果看,它们不可能是 25 匹马里的前三名。我们还了解到,「易歌尔」是所有马里跑得最快的!如果问题问的只是 25 匹马里跑得最快的是谁,那么答案就是「易歌尔」。
可我们要的是前三名。我们不光可以排除掉「红朗姆」和「菲尔拉普」,还可以排除掉第一轮比赛中所有败给它们的马。败给它们的马跑得更慢,而我们又已经知道「红朗姆」和「菲尔拉普」进不了前三了。
接下来是「奔腾」。从这场最新的比赛结果来看,它有可能是所有马里跑得第二快的。但以下可能性仍然存在:第一场比赛排在「奔腾」之后的「北舞」,是所有马里跑得第三快的。那么,最终排名就是「易歌尔」、「奔腾」和「北舞」。第一场比赛中排第三的「凯速」,现在出局了。
「易歌儿」第一次比赛时排在它后头的第二名和第三名,仍在候选之列。这两匹马的速度完全有可能比「奔腾」快,因为它们并没有比试过。总之,现在候选名单里还有 6 匹马。它们是:本场比赛的前三名;与本场比赛第一名在第一场比赛中获第二、第三名的两匹马;在第一场比赛中仅次于本场比赛第二名的一匹马。
我们已经知道「易歌儿」是跑得最快的马,因此,让它参赛没有任何意义了,于是就只剩下 5 匹马。自然,第三轮,我们会让这 5 匹马进行第 7 场,也是最后一场比赛。第 7 场比赛的前两匹马就是所有 25 匹马中跑得第二快和第三快的。
总结一下:
先进行 5 场资格赛;之后让资格赛的第一名们进行冠军争夺赛,本场比赛的获胜者就是所有马里速度最快的;再对逻辑上仍有资格的 5 匹马进行最后一场比赛。这次比赛里的前两名,就是 25 匹马里跑第二和第三快的。
4.面向对象设计题,一个借书还书系统需要哪些类,属性,方法(需要考虑很多情况)
如何准备OO Design
我认为Object-oriented design这方面的问题,面试官更多考察的是你是否有系统化的方法去分析问题并逐步细化地建立起object-oriented的模型。OO Design的题似乎在面试中并不多见。
OO Design的题目一般需要UML相关的知识做准备:
- class diagram (类图): 最常用
- sequence diagram (时序图): 最常用
- state machine diagram (状态机图): 在分析系统中某实体的状态时可能会用到。
我看过Cracking the Coding Interview (6th edition)中关于OO Design的章节。这本书里面介绍的分析和设计流程有4个步骤:
- 澄清题目中含糊不清的地方。
- 定义出核心的对象。
- 分析对象之间的关系,例如包含与被包含关系,数量上的关系,继承上的关系,等等。
- 分析对象可以具有的行为(也就是各个class的methods)。
这种分析流程是以对象为核心展开的,所以在第二步的时候就要定义问题中涉及到的对象。但我认为这样的流程在实际分析当中可能遇到的最大的问题,就是定义出的对象以及对象具有的行为可能无法完整地支持所有的业务流程。假如用ATM设计来作为例子的话,当我们只需要处理“取款”这一项业务的时候,可能我们使用以对象为核心的分析方法是可以做出完整的分析的。但是一旦业务流程增多(实际工作中的问题领域所涉及到的业务流程往往会非常多),每个流程又涉及到大量的对象,往往会遗漏掉需要对象。另一个问题是设计的对象的methods未必能完整地覆盖到所有的业务流程的需要。
因此我在做OO Design的时候,一般是以业务流程的分析为核心而展开的。这个分析过程是:
- 列举出需要设计的所有的业务流程。
- 选取一项业务流程,详细描述其内部细节的步骤。每个步骤都要用完整的主谓宾结构的句子描述。
- 将每个步骤中的主语、谓语和宾语重点标识出来。主语和宾语是将来可能建立的class,而谓语就是可能的methods。
- 构建初始的OO模型,包括所有的class,以及class之间的关联关系和数量关系。以及所有业务流程的sequence图,以及sequence图上各个method的参数和返回值。
- 改进OO模型,例如对具有共同特征的class进行抽象,抽取出公共的abstract class。
- 重复2~5步分析下一项业务流程,并且把分析出来的新内容添加到已有的OO模型中,并不断调整模型使之适应新的业务流程。直到所有的业务流程都分析完毕。
如果是学过软件工程的话,我的方法其实很简单:
- 编写详细的系统use cases。
- 识别use cases中出现的名词和动词,它们可能是OO模型中的class和methods。
还是举ATM的例子。这里我们只考虑一台ATM机的情形,于是不需要处理分布式系统中的scalability、availability和data consistency的问题。(我面试中碰到的实际问题是设计Starcraft游戏。但这个例子对很多不怎么玩游戏的同学就不适用了。)
如果我在面试中碰到这个ATM软件系统的设计题,我会这样来做:
- 列举出需要设计的业务流程:取款;存款。其实还有别的业务,比如单纯的查询余额什么的,不过这里限于篇幅,我就不列举所有的功能了。
- 对于“取款”这项业务,列出详细的执行步骤:
- 用户插入银行卡到ATM。
- ATM提示取回银行卡,并吐出银行卡。
- ATM提示输入密码。
- 用户输入密码。
- ATM验证密码。如果通过,则继续下一步;否则提示密码错误,并跳回第3步。
- ATM显示功能菜单。
- 用户点击“取款”按钮。
- ATM提示输入取款金额。
- 用户输入取款金额。
- ATM吐出指定数额的现钞。
- 标记出每个步骤中的主谓宾。在上面的步骤中,主语和宾语用下划线标识;谓语用加黑的斜体标识。
- 建立初始的OO模型。在上面的业务流程分析中,我们一共总结出如下名词:用户,银行卡,ATM,密码,功能菜单,“取款”按钮,取款金额,现钞。同时也总结出如下的动词:插入,吐出,提示,输入,验证,显示,点击。每个名词可能是OO模型中的class,每个动词可能是某个class的method。再分析不同对象之间的关联关系,于是我们可以得到一个初步的(但也是粗糙的)OO模型:
- 改进OO模型。一开始的OO模型很可能非常不完善,甚至有些部分可能还不正确。我们可以在后面不断的分析当中逐步修正。例如,“用户”很可能是属于我们所关心的系统的边界外边的,因此不应该放到系统内。“密码”或许是不需要单独建立class去描述,因为一般情况下银行的密码都是一串数字,所以很可能用一个普通的整数类型就可以表达。“取款金额”可以用Java内置的Currency类型来表示,所以也不必要单独建立class。“提示”和“显示”这两个行为其实都是在ATM的屏幕上展现信息,所以可以合并成一个行为,但此时被显示的内容就需要进行一定的抽象,例如让它们都实现一个IDisplayable接口。这样改善过的OO模型可能变成这样:
- 但这个OO模型仍然不完善。例如,“取款按钮”应该是被显示在功能菜单上,所以属于“功能菜单”看上去更合适。“点击”的操作也是实施在“功能菜单”上,所以属于“功能菜单”看上去更合适。“输入”的操作是在具体的提示消息界面中完成的,例如输入密码或取款金额,因此“输入”的操作放到“提示消息”中似乎更合适。而这样继续分析下去后,可能又可以尝试进一步把这些输入的和点击的操作抽象成某种接口。不过这些改进都可以逐步来完成。
- 考虑下一个业务流程,重复2~7步。不断地把新的业务流程加入到已有的模型中,同时不断地调整模型使之能cover目前已分析的所有流程。直到把所有业务流程都分析完毕。
总之,OO Design往往没有唯一正确的答案,但需要有一个比较系统的分析方法,让面试官相信你的分析是全面的,而不是那种毫无章法随便乱撞的方式来分析。