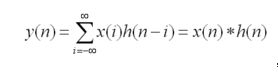我们为什么用卷积? Why should we use convolution?
Why should we use convolution?
问题限定: 仅对离散信号做分析
首先要回答什么是卷积的问题.
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions, giving the area overlap between the two functions as a function of the amount that one of the original functions is translated.
—— wikipedia
对于卷积这个东东,一般看到这两个字的人就头大,往往望而生畏.
上述定义严谨,而《The sciencetist and engineer's guide to DSP》有更为简单直接的描述
Convolution is a mathematical way of combining two signals to form a third signal.
Convolution is a formal mathematical operation, just as multiplication, addition, and integration. Addition takes two numbers and produces a third number, while convolution takes two signals and produces a third signal.
不要有太大的心理压力,它不过就是一种数学计算操作而已,用两个输入信号合成第三个信号输出.至于具体的怎么操作,后面一步步讲清楚.
先抛出个问题,然后借助解答这个问题去回答“what is convolution ?".
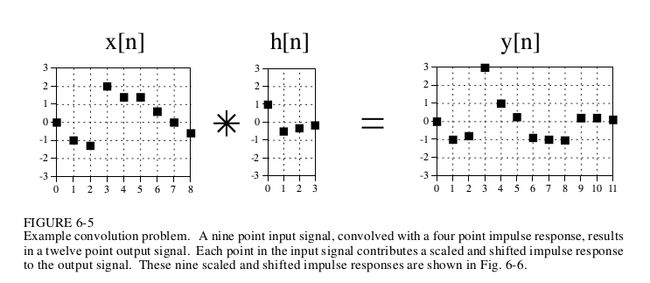
这里有两组很简单信号x[n], h[n],这两组信号做卷积处理之后得到y[n]
问题来了,x[n] 和 h[n]怎么操作就可以得到y[n]呢?
一步步分解
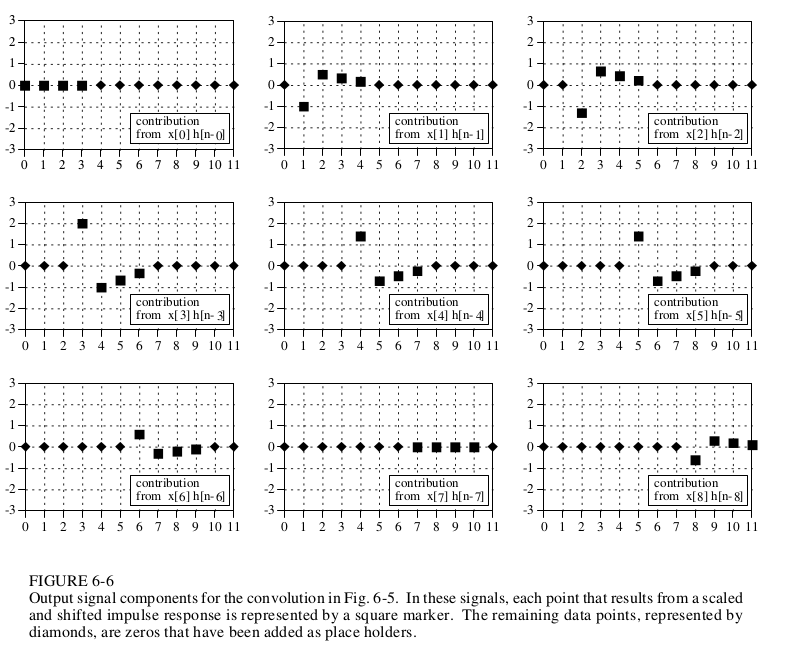
第一步,图1,x[0]h[n-0] ,这里表达的就是把x[0]依次 和h[0]~h[3]做乘法,把结果输出到此时对应的output[n](图中的方块)
第二步,图2,x[1]h[n-1] ,这里表达的就是把x[1]依次 和h[0]~h[3]做乘法,把结果输出到此时对应的output[n](图中的方块)
第三步,图3,x[2]h[n-2] ,这里表达的就是把x[2]依次 和h[0]~h[3]做乘法,把结果输出到此时对应的output[n](图中的方块)
... ...
第九步,图9,x[8]h[n-8] ,这里表达的就是把x[8]依次 和h[0]~h[3]做乘法,把结果输出到此时对应的output[n](图中的方块)
So ? 看出规律了?
之前我故意没有给出卷积的公式定义
现在再看卷积的公式定义一点清楚得多!
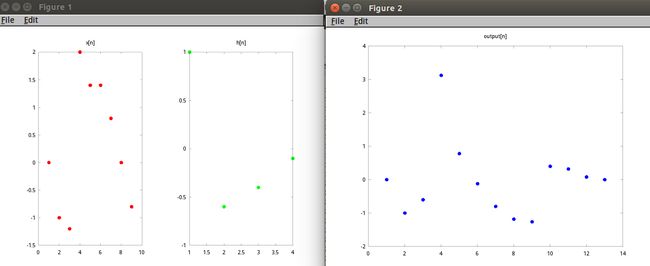
用Octave(或者 matlab)实现一个demo
利用了这幅图的数据
%code writer : EOF
%code date : 2014.09.11
%e-mail : [email protected]
%code file : convolution_input_side.m
%code purpose:
% A demo for convolution.
clear all
close all
x = [0 -1 -1.2 2 1.4 1.4 0.8 0 -0.8];
h = [1 -0.6 -0.4 -0.1];
length_x = size(x,2);
length_h = size(h,2);
output = zeros(1,length_h+length_x);
figure(1);
subplot(121);
scatter(1:length_x,x,'r','filled');
title('x[n]');
subplot(122);
scatter(1:length_h,h,'g','filled');
title('h[n]');
for tmp_1 = 1:length_x
for tmp_2 = 1:length_h
output(tmp_1+tmp_2-1) = output(tmp_1+tmp_2-1) + x(tmp_1)*h(tmp_2);
end
end
figure(2);
scatter(1:size(output,2),output,'filled');
title('output[n]');
到此,回答了什么是卷积.或者说更深刻体会了什么是卷积
为什么我们要用卷积这种东东?
Why should we use convolution? God said I just want to make filter more simple. : )
时域中的卷积就对应于频域中的乘积,那么频域中的卷积对应于时域中的乘积
卷积为滤波而生.
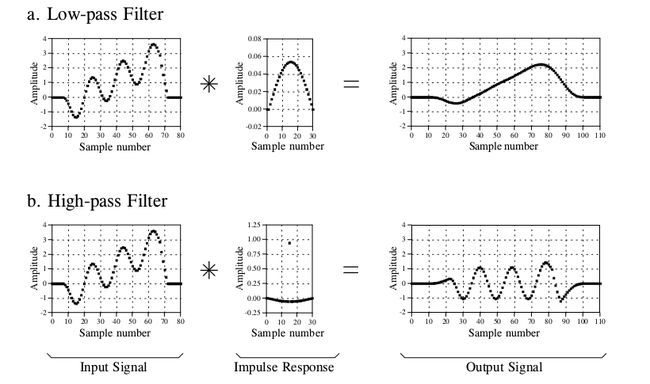
这里是两个利用卷积做滤波器的例子
图a是低通滤波,图b是高通滤波,一开始我也纳闷Input signal确实复合了多个频率的信号,怎么耶和中间的信号做卷积之后就有滤波的效果了呢?
低通滤波做卷积的这个信号有什么特点吗??
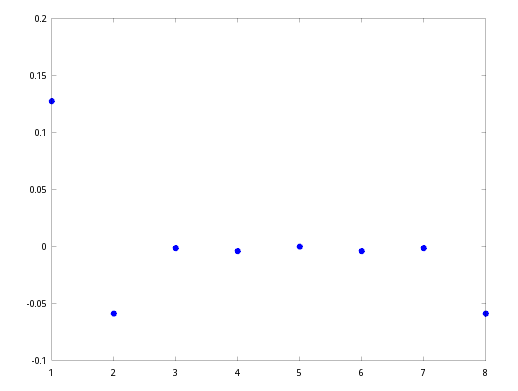
filter = [0 0.1 0.16 0.25 0.25 0.16 0.1 0]*0.125;
scatter(1:8,real(fft(filter)),'filled');
假设图中的数据是filter(我自己模拟的数据)
可以用频谱分析发现
这货的频谱是低频部分高的!抑制高频部分
把两个输入信号都变换到频率领域里面去,然后想乘,再把结果逆变换到时间领域不久得到低通滤波的结果了么!
这里再给出一种低通滤波的demo
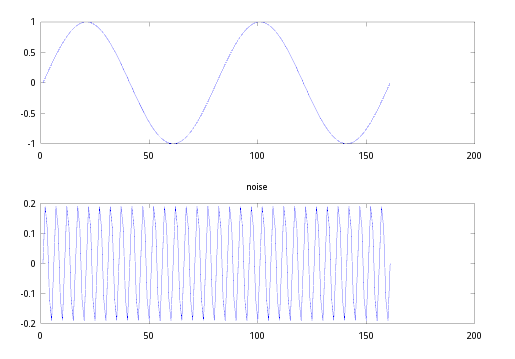
首先,利用一下两个信号合成一个输入信号,模拟带高频噪声的输入
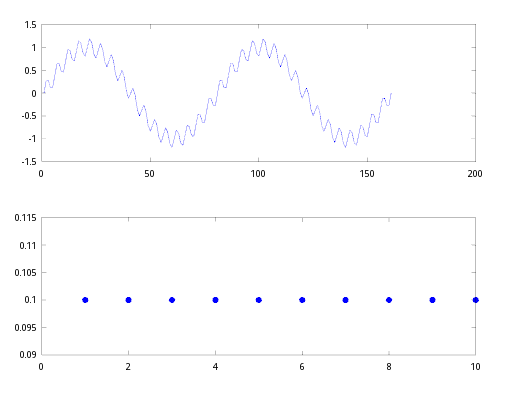
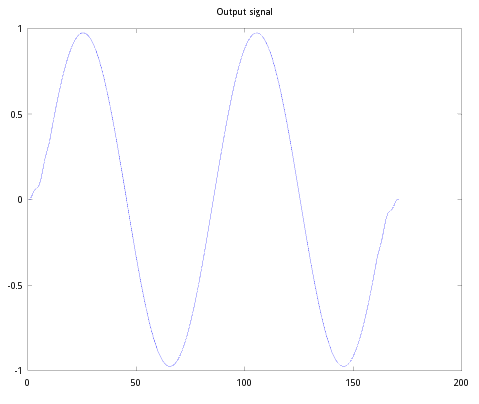
利用上面两个信号,我模拟合成了下面第一幅图的信号,作为带高频噪声的输入信号,而下面的第二幅图就是我们的做卷积的另外一个信号(低通滤波就靠它了!)
将以上两个信号做卷积得到输出信号
漂亮!几乎完美的滤去的高频噪声.
实现:
%code writer : EOF
%code date : 2014.09.11
%e-mail : [email protected]
%code file : convolution_input_side.m
%code purpose:
% Just a demo for low-pass filter by convolution.
clear all
close all
% 'y' is a simulation for original pure signal
y = sin(0.5*pi*[0:0.05:8]);
% 'u' is a simulation for noise.
u = 0.2*sin(8*pi*[0:0.05:8]);
figure(1);
subplot(211);
plot(1:size(y,2),y);
title('original pure signal'); %BUG, I don't know why I can't write title on this figure.
subplot(212);
plot(1:size(u,2),u);
title('noise');
input_signal = y + u;
x = input_signal;
h = [1 1 1 1 1 1 1 1 1 1]*0.1;
length_x = size(x,2);
length_h = size(h,2);
output_signal = zeros(1,length_h+length_x);
figure(2);
subplot(211);
plot(1:length_x,x);
subplot(212);
scatter(1:length_h,h,'filled');
for tmp_1 = 1:length_x
for tmp_2 = 1:length_h
output_signal(tmp_1+tmp_2-1) = output_signal(tmp_1+tmp_2-1) + x(tmp_1)*h(tmp_2);
end
end
figure(3);
plot(1:size(output_signal,2),output_signal);
title('Output signal');
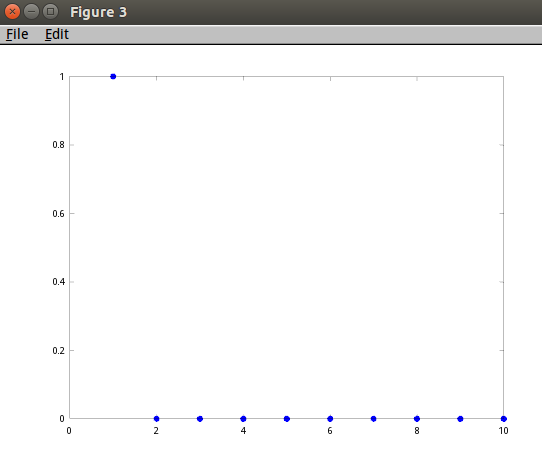
哈哈是不是想看看这个家伙的频谱图呢?
怎么它就可以低通滤波捏?下面给出了上面那个家伙的频谱图,看!低通滤波!只有在低频地带有赋值为1,其他的都是0!
当我们想要什么类型的滤波器,我们可以先构想频谱表达,然后通过逆向傅立叶变换(实际上是逆向FFT),然后得到和输入信号做卷积的因子,然后做卷积,即可实现滤波!
Why should we use convolution? God said I just want to make filter more simple. : )
update: 2014.11.13
给出卷积的C语言实现demo
/*********************************************************
code writer : EOF
code file : conv_demo.c
code date : 2014.11.13
e-mail : [email protected]
code description:
A implementation of convolution in C lanuage
**********************************************************/
#include
#include
#define DEBUG
int* init_input(int number)
{
if(number <= 0)
{
printf("number < 0! in function %s\n",__FUNCTION__);
return NULL;
}
int* p_input = (int*)malloc(sizeof(int)*number);
if(!p_input)
{
printf("malloc error!\n");
return NULL;
}
int temp = 0;
for(temp = 0;temp < number;temp++)
{
if(scanf("%d",(p_input+temp)) < 0)
{
return NULL;
}
}
return p_input;
}
int* init_unit_responce(int number)
{
if(number <= 0)
{
printf("number < 0! in function %s\n",__FUNCTION__);
return NULL;
}
int* p_unit_responce = (int*)malloc(sizeof(int)*number);
if(!p_unit_responce)
{
printf("malloc error!\n");
return NULL;
}
int temp = 0;
for(temp = 0;temp < number;temp++)
{
if(scanf("%d",(p_unit_responce +temp)) < 0)
{
return NULL;
}
}
return p_unit_responce;
}
void release(int* p_input,int* p_unit_responce)
{
free(p_input);
free(p_unit_responce);
}
int* conv(int* p_input,int ip_num,int* p_unit_responce,int ur_num)
{
if(!p_input || !p_unit_responce || ip_num <= 0 || ur_num <= 0)
{
printf("Data losted!\n");
return NULL;
}
int* p_output = (int*)malloc(sizeof(int)*(ip_num + ur_num - 1));
if(!p_output)
{
printf("malloc error! in function %s\n",__FUNCTION__);
return NULL;
}
int tmp = 0;
int idx = 0;
int sum = 0;
for(tmp = 0;tmp < ip_num + ur_num -1;tmp++)
{
sum = 0;
for(idx = 0; (tmp - idx) >= 0 && idx < ur_num;idx++)
{
if((tmp -idx) < ip_num)
{
sum += p_unit_responce[idx]*p_input[tmp-idx];
}
}
*(p_output + tmp) = sum;
#ifdef DEBUG
printf("\t%d",sum);
#endif
}
#ifdef DEBUG
printf("\n");
#endif
return p_output;
}
int main()
{
int ip_num = 0;
printf("Hey guys! Just input the size of input-data!\n");
while(!scanf("%d",&ip_num))
{
printf("input data type error! Input again!\n");
getchar();// clear the '\n' after we inputed.
}
int* p_input = NULL;
p_input = init_input(ip_num);
if(!p_input)
{
goto out;
}
printf("What about the size of unit-responce!\n");
int ur_num = 0;
while(!scanf("%d",&ur_num))
{
printf("input data type error! Input again!\n");
getchar();// clear the '\n' after we inputed.
}
int* p_unit_responce = NULL;
p_unit_responce = init_unit_responce(ur_num);
if(!p_unit_responce)
{
goto out;
}
conv(p_input,ip_num,p_unit_responce,ur_num);
out:
release(p_input,p_unit_responce);
return 0;
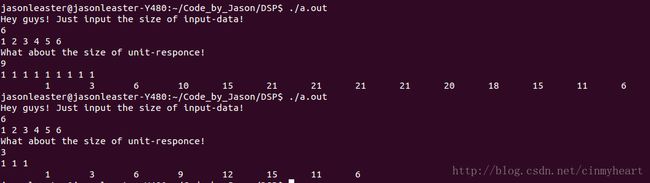
} 测试结果:
用matlab的conv函数来检验我们程序的正确性,对比可知,我们程序实现是正确的。