启发式算法笔记01_随机算法（Randomised Algorithms）

本篇为在University of Birmingham 学习Advanced Nature-Inspired Search and Optimisation课程中的笔记之一
This is one of the notes from the Advanced Nature-Inspired Search and Optimisation course at the University of Birmingham

[toc]

1 问题引出——螺栓螺母的匹配问题

1.1 一个螺栓与n个螺母(Matching one Bolt to n Nuts)

• The everyday problem: given one bolt and a collection of n nuts of different sizes, find a nut match the bolt
• In mathematical form: given an array of n elements, find the first element of which the value equals to x
• Q: How to solve it using an algorithm? How to solve it efficiently?

1.2 n个螺栓与n个螺母(the real Nuts and Bolts Problem)

• A disorganized carpenter has a collection of n nuts of distinct sizes and n bolts and would like to find the corresponding pairs of bolts and nuts. Each nut matches exactly one bolt (and vice versa), and he can only compare nuts to bolts, i.e., he can neither compare nuts to nuts nor bolts to bolts.
• Can you help the carpenter match the nuts and bolts quickly?
• This is called Nuts and Bolts Problem or Lock and Key problem.
• Q: How to formulate the problem? How to solve it using an algorithm? How to solve it efficiently?

---

2 方案介绍——随机算法 (Randomised Algorithms)

“For many problems, a randomised algorithm is the simplest, the fastest or both.” —— Prabhakar Raghavan, Vice President of Engineering at Google.

2.1 算法一览_Categories of algorithms by design paradigm

1. 分治算法(Divide and conquer algorithms, e.g., quicksort algorithm, Merge-Sort)
2. 数学规划算法(Mathematical programming algorithms, e.g., linear programming, Multi-objective programming, Dynamic programming algorithms)
3. 搜索和枚举算法(Search and enumeration algorithms)
   1. 蛮力算法_Brute force algorithms, enumerating all possible candidate solutions and check
   2. 改进的蛮力算法_Improved brute force algorithms, e.g., branch and bound algorithms
   3. 启发式算法_Heuristic algorithms
      1. 局部搜索_Local search, e.g., greedy search
      2. 随机算法_Randomised algorithms, which include Evolutionary Computation, etc.

2.2 启发式算法与随机算法_Heuristic Algorithms & Randomised Algorithms

1). 启发式在计算机中的解释:

一种（通常是简单的）算法，可以在合理的时间内为问题提供足够好的解决方案 (A (usually simple) algorithm that produces a good enough solution for a problem in a reasonable time frame)

1. 解决方案（通常）不是最佳方案，但令人满意：
   1. 更快：替代蛮力（穷举）搜索
   2. 权衡最优性，完整性，准确性或精度以提高速度。
2. 通常用于解决其他算法难以解决的问题，例如蛮力算法
3. 包括确定性（例如本地搜索_local search algorithm）和随机算法(Randomised Algorithm)

2). 随机算法

1. Randomised algorithm: An heuristic algorithm that makes random choices during execution to produce a result_随机选择产生结果
   1. Takes a source of random numbers to make random choices
   2. Behaviour, e.g., output or running time can vary even on a fixed input
2. The goal: design an algorithm and analyse it to show that its behaviour is likely to be good, on every input

3). 随机算法_Randomised Algorithms & 确定性算法_Deterministic Algorithms

graph LR
input => Algorithm
Algorithm=>output

图1. Deterministic Algorithms

graph LR
input --> Algorithm
Random_number --> Algorithm
Algorithm-->output

图2. Randomised Algorithms

---

3 解决方案——拉斯维加斯算法与蒙特卡洛算法

3.1 一个螺栓与n个螺母(Matching one Bolt to n Nuts)

• 对于第一个螺栓与n个螺母(Matching one Bolt to n Nuts)的问题，解决思想为使用随机数找到问题的解决方案(Using random numbers to find a solution to a problem)

• 将其抽象为数学问题即为: 给定n个元素的数组，找到其值等于x的第一个元素(The problem: given an array of n elements, find the first element of which the value equals to x)

• 具有代表性的两个解决算法分别是拉斯维加斯算法和蒙特卡洛算法

1). 介绍 拉斯维加斯算法_Las Vegas algorithm 与蒙特卡洛算法_Monte Carlo algorithm

# 拉斯维加斯算法_Las Vegas algorithm
begin
    repeat
        Randomly select one element a out of n elements. 
    until a == x
end

如上所述，拉斯维加斯算法始终返回正确的结果。上面的代码说明了此属性。变量a是随机生成的；生成a后，使用a索引n个元素(数组)中比较x。如果该索引包含值x，则返回a；该算法将重复此过程，直到找到x。尽管可以保证使用此Las Vegas算法来找到正确的答案，但它没有固定的运行时间。

# 蒙特卡洛算法_Monte Carlo algorithm
begin
    i := 0 
    repeat
        Randomly select one element a out of n elements.
        i := i + 1
    until (a == x)||(i == k)
end

由于拉斯维加斯直到在数组中找到x才结束，它是以运行次数来赌博。另一方面，Monte Carlo运行k次，这意味着不一定在执行代码的k次循环中，在数组中找到“x”；意味着它可能会找到解决方案，也可能不会。因此，与拉斯维加斯不同的是，蒙特卡洛（Monte Carlo）在正确性上赌博。

2). 比较 拉斯维加斯算法_Las Vegas algorithm 与蒙特卡洛算法_Monte Carlo algorithm

1. 拉斯维加斯算法_Las Vegas algorithm: 始终提供正确结果的随机算法，一次运行到另一次运行的唯一变化是运行次数(A randomised algorithm that always gives correct results, the only variation from one run to another is the running time)

2. 蒙特卡洛算法_Monte Carlo algorithm: 一种随机算法，其运行次数是确定性的，但其结果在一定（通常较小）概率下可能不正确。(A randomised algorithm whose running time is deterministic, but whose results may be incorrect with a certain (typically small) probability.)

3. 不同点:

   1. 蒙特卡洛算法运行固定数量的次数（Monte Carlo algorithm runs for a fixed number of steps）
   2. 拉斯维加斯算法无限循环运行，直到找到正确的结果（Las Vegas algorithm runs in an infinite loop until the correct results are found）
   3. 可以使用提前终止将拉斯维加斯算法转换为蒙特卡洛算法（Las Vegas algorithm can be converted into Monte Carlo algorithm using early termination）

3). 总结 拉斯维加斯算法_Las Vegas algorithm 与蒙特卡洛算法_Monte Carlo algorithm

• 元素搜索问题非常简单，但是
  1. 对于确定性顺序（线性）搜索算法，例如，从头开始逐一搜索数组：
     1. 平均时间复杂度:
     2. 最坏时间复杂度:
  2. 对于拉斯维加斯算法_Las Vegas algorithm：
     1. 平均时间复杂度: 取决于输入; 如果一半数组包含0,另一半包含1，则查找第一个元素的值等于1的平均时间复杂度为
     2. 最坏时间复杂度: 无限（Unbound）
  3. 对于蒙特卡洛算法_Monte Carlo algorithm：
     1. 平均时间复杂度:
     2. 最坏时间复杂度:
     3. 会有找不到元素的可能性。

3.2 n个螺栓与n个螺母(the real Nuts and Bolts Problem)

• 一个没有条理的木匠有n个不同大小的螺母和n个螺栓的集合，并希望找到相应的螺栓和螺母配对。每个螺母正好匹配一个螺栓（反之亦然），并且他只能将螺母与螺栓进行比较，即，他既不能将螺母与螺母进行比较，也不能将螺栓与螺栓进行比较。(A disorganized carpenter has a collection of n nuts of distinct sizes and n bolts and would like to find the corresponding pairs of bolts and nuts. Each nut matches exactly one bolt (and vice versa), and he can only compare nuts to bolts, i.e., he can neither compare nuts to nuts nor bolts to bolts.)
• 如果采用暴力算法(将每个螺母与所有螺栓进行比较以找到匹配的螺栓), 时间复杂度为
• 本节推荐使用随机化快速排序_Randomised quicksort algorithm

1). 快速排序_Quicksort algorithm

快速排序: 给定n个数字组成的数组A，按递增顺序对数字进行排序 (Given a array A of n numbers, sort the numbers in increasing order)

快速排序图解

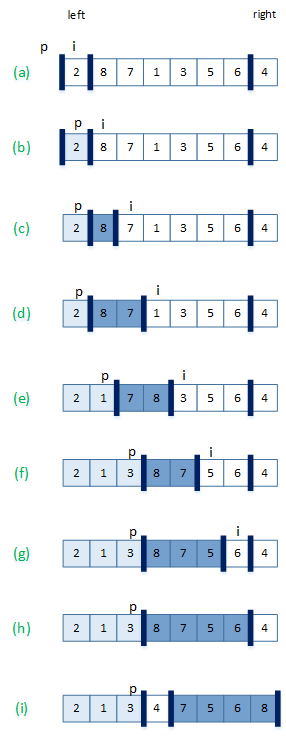
# 快速排序_Quicksort algorithm
less, equal, greater := three empty arrays 
if length(array) > 1
    pivot := select an element of array 
    for each x in array
    if x < pivot then add x to less
    if x = pivot then add x to equal 
    if x > pivot then add x to greater
quicksort(less)
quicksort(greater)
array := concatenate(less, equal, greater)

• 平均时间复杂度:（n是数组的大小）
  {Deterministic quicksort algorithm time complexity: on average for a random permutation array (n is the size of the array)}
• 最坏时间复杂度:

2). 随机化快速排序_Randomised quicksort algorithm

• 随机化快速排序算法: 随机选择枢轴(Selecting a pivot randomly)
• 平均时间复杂度:
• 最坏时间复杂度:
• 证明_Proof: Probabilistic Analysis and
  Randomized Quicksort
• n个螺栓与n个螺母问题(the real Nuts and Bolts Problem)的具体方案

---

4 扩展

4.1 随机算法的应用

1. 数学:

   1. 数论，例如素数检验_Number theory, e.g., primality test
   2. 计算几何：图形算法，例如最小分割_Computational Geometry: graph algorithms, e.g., minimum cut
   3. 线性代数：矩阵计算_Linear algebra: matrix computations

2. 计算机科学:

   1. 数据分析：网页排名_Data analysis: PageRank
   2. 并行计算：避免死锁_Parallel computing: Deadlock avoidance
   3. 优化：自然启发的优化和搜索算法_Optimisation: Nature inspired Optimisation and Search algorithms

3. 计算生物: DNA read alignment

4.2 随机算法的优缺点

1. 优点
   1. 简单性：通常非常容易实现(Usually very easy to implement)
   2. 性能：通常以高概率产生（接近）最佳解决方案(Usually produce (near-) optimum solutions with high probability)
2. 缺点
   1. 以有限的概率得到错误的答案(Getting a wrong answer with a finite probability.)
      1. 解决方案：重复算法
   2. 难以分析运行时间和获得错误解决方案的概率(Difficult to analyse the running time and probability of getting an incorrect solution)
   3. 不可能获得真正的随机数(Impossible to get truly random numbers)

4.3 阅读材料

1. Motwani, Rajeev; Raghavan, Prabhakar (1995). Randomized Algorithms. New York: Cambridge University Press. ISBN 0-521-47465-5.
2. Richard M. Karp (1991), An introduction to randomized algorithms, 34, Discrete Mathematics.
3. Michael W. Mahoney(2011),Randomized algorithms for matrices and data.