《算法文章汇总》
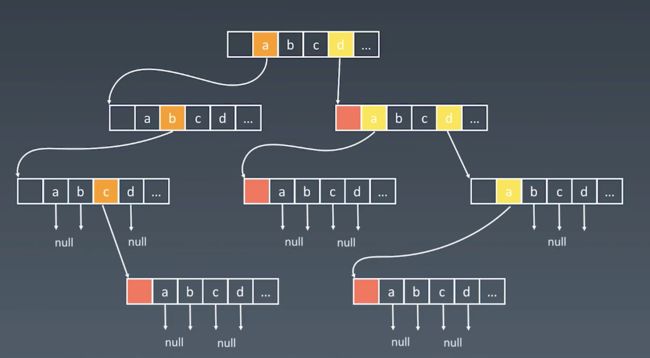
字典树,即Trie树,又称单词查找树或键树,是一种树形结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
基本性质
1.节点本身不存完整单词
2.从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
3.每个节点的所有子节点路径代表的字符都不相同
trie核心思想是空间换时间
利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的
节点的内部实现
实现Trie
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
向 Trie 树中插入键
我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况:
链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
链接不存在。创建一个新的节点,并将它与父节点的链接相连,该链接与当前的键字符相匹配。
重复以上步骤,直到到达键的最后一个字符,然后将当前节点标记为结束节点,算法完成。
class Trie {
class TrieNode {
//结点数
private TrieNode[] links;
private final int R = 26;
private boolean isEnd;
public TrieNode(){
links = new TrieNode[R];
}
public boolean containsKey(char ch){
return links[ch - 'a'] != null;
}
public TrieNode get(char ch){
return links[ch - 'a'];
}
public void put(char ch, TrieNode node){
links[ch - 'a'] = node;
}
public void setIsEnd(){
isEnd = true;
}
public boolean isEnd(){
return isEnd;
}
}
private TrieNode root;
public Trie(){
root = new TrieNode();
}
//Inserts a word into the trie
public void insert(String word){
TrieNode node = root;
for (int i = 0;i单词搜索II
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words,找出所有同时在二维网格和字典中出现的单词。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:
输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出:["eat","oath"]
示例 2:
输入:board = [["a","b"],["c","d"]], words = ["abcb"]
输出:[]
并查集
Quick Union Ranks
Path Halving Path Spliting
/**
* 项目名称:Arithmetic
* 类 名 称:UnionFind_QU_Rank
* 类 描 述:TODO
* 创建时间:2021/4/27 7:53 PM
* 创 建 人:cloud
*/
public class UnionFind_QU_Rank extends UnionFind_QU {
private int[] ranks;
public UnionFind_QU_Rank(int capacity) {
super(capacity);
ranks = new int[capacity];
//以i为根节点的这棵树的高度
for (int i=0;i ranks[p2]){
parents[p2] = p1;
}else{
parents[p1] = p2;
ranks[p2] ++;
}
}
}
省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
import org.junit.Test;
/**
* 项目名称:Arithmetic
* 类 名 称:UnionFind0
* 类 描 述:TODO
* 创建时间:2021/4/27 10:50 PM
* 创 建 人:cloud
*/
public class Solution0{
public class UnionFind0 {
public int[] parents;
public int sizes;//集合数量
public UnionFind0(int n) {
parents = new int[n];
for (int i = 0; i < n; i++) {
parents[i] = i;
}
sizes = n;
}
//快速查找根节点:路径压缩,使路径上所有节点都指向根节点,从而降低树的高度
public int find(int v) {
rangeCheck(v);
if (parents[v] != v) {
parents[v] = find(parents[v]);
}
return parents[v];
}
//是不是相同的集合,联通的点
public boolean isSame(int v1, int v2) {
return find(v1) == find(v2);
}
//合并v1,v2
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if (p1 == p2) return;
if (p1 != p2) {
parents[p1] = p2;
sizes--;
}
}
//检查边界
public void rangeCheck(int v) {
if (v < 0 || v > parents.length) {
throw new IllegalArgumentException("v is out of bounds");
}
}
}
public int findCircleNum(int[][] isConnected) {
//初始化并查集
UnionFind0 unionFind0 = new UnionFind0(isConnected.length);
for (int i = 0; i < isConnected.length; i++) {
for (int j = i + 1; j < isConnected.length; j++) {
if (isConnected[i][j] == 1) {
unionFind0.union(i, j);
}
}
}
return unionFind0.sizes;
}
@Test
public void testCombineFindSet() {
// int[][] isConnected = {{1,1,0},{1,1,0},{0,0,1}};
// System.out.println(findCircleNum(isConnected));
// int[][] isConnected1 = {{1,0,0},{0,1,0},{0,0,1}};
// System.out.println(findCircleNum(isConnected1));
int[][] isConnected2 = {{1,1,1,1,1},{1,1,1,1,1},{1,1,1,1,1},{1,1,1,1,1},{1,1,1,1,1}};
System.out.println(findCircleNum(isConnected2));
}
}
岛屿数量
public class UnionFind1{
//根节点数组
public int[] parents;
//集合数量
public int sizes;
UnionFind1(int capacity){
parents = new int[capacity];
for (int i = 0;i parents.length)
throw new IllegalArgumentException("v is out of bounds");
}
//路径减半:将一条线上面的所有节点都指向祖父节点,压缩了树的高度
public int find(int v){
rangeCheck(v);
while(v !=parents[v]){
parents[v] = parents[parents[v]];
v = parents[v];
}
return v;
}
//快速合并两个集合,集合的根节点中一方指向另外一方
public void union(int v1,int v2){
int p1 = find(v1);
int p2 = find(v2);
//同一个集合,不需要合并
if (p1 == p2) return;
if (p1 != p2){
parents[p1] = p2;
sizes--;
}
}
}
//岛屿数量,集合数量
public int numIslands(char[][] grid) {
//如果是一行一列
if (grid.length == 0 || grid == null) return 0;
int row = grid.length;
int col = grid[0].length;
int water = 0;//水域(0)个数
UnionFind1 unionFind1 = new UnionFind1(row * col);
for (int i = 0;i=0 && y>=0 && x|
被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
思路:我们的思路是把所有边界上的 OO 看做一个连通区域。遇到 OO 就执行并查集合并操作,这样所有的 OO 就会被分成两类
和边界上的 OO 在一个连通区域内的。这些 OO 我们保留。
不和边界上的 OO 在一个连通区域内的。这些 OO 就是被包围的,替换。
由于并查集我们一般用一维数组来记录,方便查找 parants,所以我们将二维坐标用 node 函数转化为一维坐标。
class Solution {
public class UnionFind2{
//根节点数组
public int[] parents;
UnionFind2(int capacity){
parents = new int[capacity];
for (int i=0;i parents.length)
throw new IllegalArgumentException("v is out of bound");
}
}
public int row;
public int column;
public void solve(char[][] board) {
row = board.length;
column = board[0].length;
if (row == 0 || column == 0) return;
UnionFind2 unionFind2 = new UnionFind2(row * column + 1);
//标记边界连通为一个区域
int dummy = row * column;
for (int i = 0;i 0 && board[i-1][j] == 'O'){
unionFind2.union(node(i,j),node(i-1,j));
}
if (i < row - 1 && board[i+1][j] == 'O'){
unionFind2.union(node(i,j),node(i+1,j));
}
if (j > 0 && board[i][j -1] == 'O'){
unionFind2.union(node(i,j),node(i,j-1));
}
if (j < column - 1 && board[i][j+1] == 'O'){
unionFind2.union(node(i,j),node(i,j+1));
}
}
}
}
for (int i = 0;i