1 Multi-Paxos
朴素Paxos算法通过多轮的Prepare/Accept过程来确定一个值,Lamport称这整个过程为一个Instance。Multi-Paxos是通过Paxos算法来确定很多个值,而且这些值的顺序在各个节点完全一致。概括来讲就是确定一个全局顺序。
1.1 确定多个值
多个Instance怎么运作?首先我们先构建最简易的模式,各个Instance独立运作下面的例子引自知乎Paxos理论介绍(2): Multi-Paxos与Leader的Multi-Paxos部分。
每个Instance独立运作一个朴素Paxos算法,我们保证仅当Instance i的值被确定后,方可进行i+1的Paxos算法,这样我们就保证了Instance的有序性。
但这样效率是比较差的,众所周知朴素Paxos算法的Latency很高,Multi-Paxos算法希望找到多个Instance的Paxos算法之间的联系,从而尝试在某些情况去掉Prepare步骤。
2 Multi-Paxos算法描述
下面我尝试描述一个Sample的演进情况来阐述这个算法,因为这个算法的要点其实非常简单,而且无需更多证明。
首先我们定义Multi-Paxos的参与要素:
- 3个参与节点 A/B/C.
- Prepare(b)=Prepare(bal) NodeA节点发起Prepare携带的编号。
- Promise(b)=Promise(bal) NodeA节点承诺的编号。
- Accept(b)=Accept(bal) NodeA节点发起Accept携带的编号。
1(A)的意思是A节点产生的编号1,2(B)代表编号2由B节点产生。绿色表示Accept通过,红色表示拒绝。
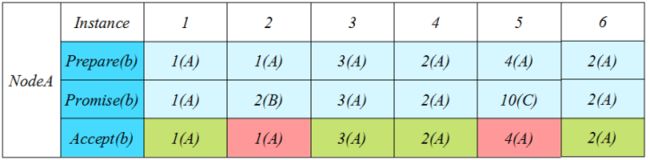
下图描述了A/B/C三个节点并行提交的演进过程:
这种情况下NodeA节点几乎每个Instance都收到其他节点发来的Prepare,导致Promise编号过大,迫使自己不断提升编号来Prepare。这种情况并未能找到任何的优化突破口。
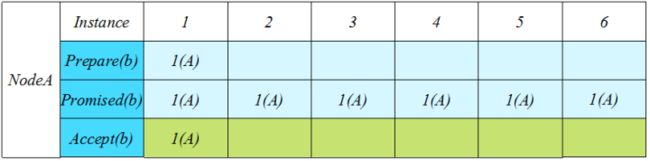
下图描述了只有A节点提交的演进过程:
这种情况我们会立刻发现,在没有其他节点提交的干扰下,每次Prepare的编号都是一样的。于是乎我们想,为何不把Promised(b)变成全局的?来看下图:
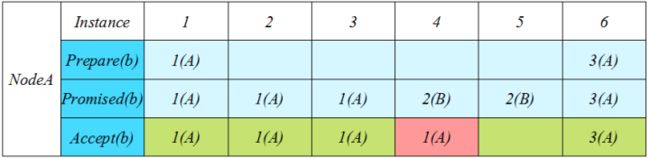
假设我们在Instance i进行Prepare(b),我们要求对这个b进行Promise的生效范围是Instance[i, ∞),那么在i之后我们就无需在做任何Prepare了。可想而知,假设上图Instance 1之后都没有任何除NodeA之外其他节点的提交,我们就可以预期接下来Node A的Accept都是可以通过的。那么这个去Prepare状态什么时候打破?我们来看有其他节点进行提交的情况:
Instance 4出现了B的提交,使得Promised(b)变成了2(B), 从而导致Node A的Accept被拒绝。而NodeA如何继续提交?必须得提高自己的Prepare编号从而抢占Promised(b)。这里出现了很明显的去Prepare的窗口期Instance[1,3],而这种期间很明显的标志就是只有一个节点在提交。
2.1 Leader的作用
不Prepare直接Accept为啥是安全的
在一个Leader提交proposal的前提下,不会有其他Proposer提交,那么就不会出现Acceptor promised的最大编号大于proposal中所带编号的情况,同样也不会出现Acceptor accept的编号大于proposal中所带编号的情况。因此这么做是安全的。
不Prepare直接Accept有什么好处
To achieve this, the round number I is included along with each value which is incremented in each round by the same Leader. Multi-Paxos reduces the failure-free message delay (proposal to learning) from 4 delays to 2 delays.
这句不太会翻译,但大概的意思应该就是:Multi-Paxos通过改变Promised(b)的生效范围至全局的Instance,从而使得一些唯一节点的连续提交获得去Prepare的效果。
2.1 选举一个Leader
下面是知乎文章中介绍的一个方法,个人感觉这个没有一个标准的设计,暂时参考这个。
为何还要说Leader,虽然Multi-Paxos允许并行提交,但这种情况下效率是要退化到朴素Paxos的,所以我们并不希望长时间处于这种情况,Leader的作用是希望大部分时间都只有一个节点在提交,这样才能最大发挥Mulit-Paxos的优化效果。
怎么得到一个Leader,真的非常之简单,Lamport的论文甚至的不屑一提。我们观察Multi-Paxos算法,首先能做Accept(b)必然是b已经被Promised了,而连续的Accept(b)被打断,必然是由于Promised(b)被提升了,也就是出现了其他节点的提交(提交会先Prepare从而提升b)。那么重点来了,如何避免其他节点进行提交,我们只需要做一件事即可完成。
收到来自其他节点的Accept,则进行一段时间的拒绝提交请求。
这个解读起来就是各个节点都想着不要去打破这种连续的Accept状态,而当有一个节点在连续的Accept,那么其他节点必然持续不断的拒绝请求。这个Leader就这样无形的被产生出来了,我们压根没有刻意去“选举”,它就是来自于Multi-Paxos算法。
题外话:为何网上出现很多非常复杂的选举Leader算法,有的甚至利用Paxos算法去选举Leader,我觉的他们很有可能是没有完全理解Multi-Paxos,走入了必须有Leader这个误区。
用Paxos算法来进行选举是有意义的,但不应该用在Leader上面。Paxos的应用除了写之外,还有很重要的一环就是读,很多时候我们希望要读到Latest,通常的做法就是选举出一个Master。Master含义是在任一时刻只能有一个节点认为自己是Master,在这种约束下,读写我都在Master上进行,就可以获得Latest的效果。Master与Leader有本质上的区别,要达到Master这种强一致的唯一性,必须得通过强一致性算法才能选举出来。而当我们实现了Paxos算法后,选举Master也就变得非常简单了,会涉及到一些租约的东西,后面再分享。
3 算法示例
正常执行成功
Multi-Paxos实际上是Basic Baxos的多instance执行。下图是一个初始的Leader(实际上是一个Proposer)执行一次Basic Baxos的过程。
Client Proposer Acceptor Learner
| | | | | | | --- First Request ---
X-------->| | | | | | Request
| X--------->|->|->| | | Prepare(N)
| |<---------X--X--X | | Promise(N,I,{Va,Vb,Vc})
| X--------->|->|->| | | Accept!(N,I,V)
| |<---------X--X--X------>|->| Accepted(N,I,V)
|<---------------------------------X--X Response
| | | | | | |
where V = last of (Va, Vb, Vc).
Phase 1 去掉之后的Multi-Paxos
在这个case中,接下来的instance(第I+1个instance)都使用的同一个Leader,因此直接跳过了phase1(接下来instance中Basic Paxos协议的phase 1,即省略prepare阶段),其中Leader应该是稳定的,不能宕机或者故障。
这里出现故障应该只是退化到Basic Paxos的情况。
Client Proposer Acceptor Learner
| | | | | | | --- Following Requests ---
X-------->| | | | | | Request
| X--------->|->|->| | | Accept!(N,I+1,W)
| |<---------X--X--X------>|->| Accepted(N,I+1,W)
|<---------------------------------X--X Response
| | | | | | |
Multi-Paxos when roles are collapsed
A common deployment of the Multi-Paxos consists in collapsing the role of the Proposers, Acceptors and Acceptors to "Servers". So, in the end, there are only "Clients" and "Servers".
意思就是Proposers,Acceptors,Acceptors没有明确的角色区分,统称为Servers。Server可以扮演以上三种任何角色,这样部署起来就只有Clients和Servers区分。
Client Servers
| | | | --- First Request ---
X-------->| | | Request
| X->|->| Prepare(N)
| |<-X--X Promise(N, I, {Va, Vb})
| X->|->| Accept!(N, I, Vn)
| X<>X<>X Accepted(N, I)
|<--------X | | Response
| | | |
Leader固定之后的一个instance
固定Leader之后,且角色合并成了Server跟Client。
Client Servers
X-------->| | | Request
| X->|->| Accept!(N,I+1,W)
| X<>X<>X Accepted(N,I+1)
|<--------X | | Response
| | | |