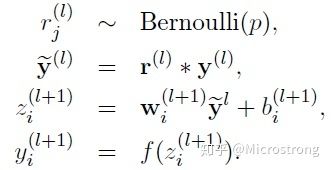Dropout:随即失活
文章目录
- Dropout简介
-
- 1.1 Dropout出现的原因
- 1.2 什么是Dropout
- 2. Dropout工作流程及使用
-
- 2.1 Dropout具体工作流程
- 2.2 Dropout在神经网络中的使用
- 3. 为什么说Dropout可以解决过拟合?
- 4. Dropout在Pytorch中的源码分析
- 思考:
- 总结:
Dropout简介
1.1 Dropout出现的原因
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
容易过拟合
费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
1.2 什么是Dropout
在2012年,Hinton在其论文《Improving neural networks by preventing co-adaptation of feature detectors》中提出Dropout。当一个复杂的前馈神经网络被训练在小的数据集时,容易造成过拟合。为了防止过拟合,可以通过阻止特征检测器的共同作用来提高神经网络的性能。
在2012年,Alex、Hinton在其论文《ImageNet Classification with Deep Convolutional Neural Networks》中用到了Dropout算法,用于防止过拟合。并且,这篇论文提到的AlexNet网络模型引爆了神经网络应用热潮,并赢得了2012年图像识别大赛冠军,使得CNN成为图像分类上的核心算法模型。
随后,又有一些关于Dropout的文章《Dropout:A Simple Way to Prevent Neural Networks from Overfitting》、《Improving Neural Networks with Dropout》、《Dropout as data augmentation》。
从上面的论文中,我们能感受到Dropout在深度学习中的重要性。那么,到底什么是Dropout呢?
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
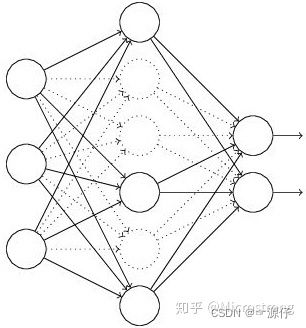
Dropout说的简单一点就是:我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征,如图1所示。

2. Dropout工作流程及使用
2.1 Dropout具体工作流程
假设我们要训练这样一个神经网络,如图2所示。
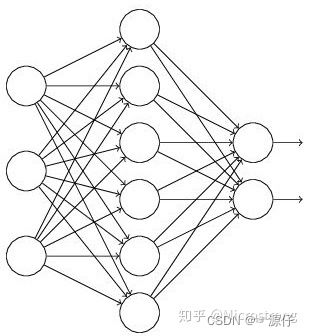
输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后,过程变成如下:
首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(图3中虚线为部分临时被删除的神经元)
然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
然后继续重复这一过程:
- 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
- 对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数(w,b) (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
不断重复这一过程。
2.2 Dropout在神经网络中的使用
Dropout的具体工作流程上面已经详细的介绍过了,但是具体怎么让某些神经元以一定的概率停止工作(就是被删除掉)?代码层面如何实现呢?
下面,我们具体讲解一下Dropout代码层面的一些公式推导及代码实现思路。
(1)在训练模型阶段
无可避免的,在训练网络的每个单元都要添加一道概率流程。

对应的公式变化如下:
上面公式中Bernoulli函数是为了生成概率r向量,也就是随机生成一个0、1的向量。
代码层面实现让某个神经元以概率p停止工作,其实就是让它的激活函数值以概率p变为0。比如我们某一层网络神经元的个数为1000个,其激活函数输出值为y1、y2、y3、…、y1000,我们dropout比率选择0.4,那么这一层神经元经过dropout后,1000个神经元中会有大约400个的值被置为0。
注意: 经过上面屏蔽掉某些神经元,使其激活值为0以后,我们还需要对向量y1……y1000进行缩放,也就是乘以1/(1-p)。如果你在训练的时候,经过置0后,没有对y1……y1000进行缩放(rescale),那么在测试的时候,就需要对权重进行缩放,操作如下。
(2)在测试模型阶段
预测模型的时候,每一个神经单元的权重参数要乘以概率p。
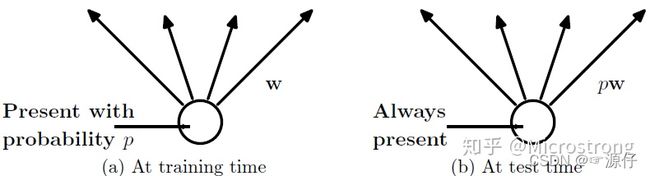
测试阶段Dropout公式:
W t e s t l W^{l} _{test} Wtestl = p W l pW^l pWl
3. 为什么说Dropout可以解决过拟合?
取平均的作用:
先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
减少神经元之间复杂的共适应关系:
因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
Dropout类似于性别在生物进化中的角色:
物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
4. Dropout在Pytorch中的源码分析
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import sys, os
hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)
from PYTORCH.Deep_eye.Pytorch_Camp_master.hello_pytorch.tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter
set_seed(1) # 设置随机种子
n_hidden = 200
max_iter = 2000
disp_interval = 400
lr_init = 0.01
# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):
w = 1.5
train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
return train_x, train_y, test_x, test_y
train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))
# ============================ step 2/5 模型 ============================
# 输出层之前一般不加Dropout
class MLP(nn.Module):
def __init__(self, neural_num, d_prob=0.5):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.) # d_prob=0.,不进行Dropout
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5) # Dropout概率取0.5
# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)
# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()
# ============================ step 5/5 迭代训练 ============================
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_reglar.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_reglar.step()
if (epoch+1) % disp_interval == 0:
net_prob_0.eval() # net采用测试状态
net_prob_05.eval()
# 可视化
for name, layer in net_prob_0.named_parameters():
writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
writer.add_histogram(name + '_data_normal', layer, epoch)
for name, layer in net_prob_05.named_parameters():
writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)
writer.add_histogram(name + '_data_regularization', layer, epoch)
test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)
# 绘图
plt.clf()
plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')
plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')
plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})
plt.ylim((-2.5, 2.5))
plt.legend(loc='upper left')
plt.title("Epoch: {}".format(epoch+1))
plt.show()
plt.close()
net_prob_0.train()
net_prob_05.train()
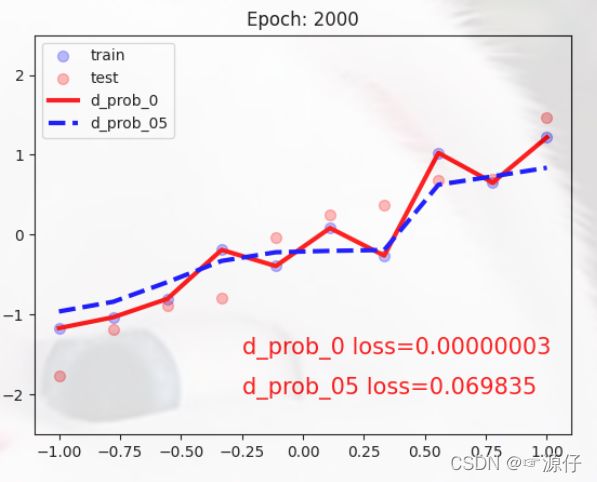
红色线的Loss很低,已经完全过拟合了。
蓝色曲线加入了Dropout,就明显减轻了过拟合,较为平滑。
Dropout控制权重的尺度:(收缩权重的功能)
dropout 将产生收缩权重的平方范数的效果,和L2正则化类似,实施 dropout的结果是它会压缩权重,并完成一些预防过拟合的外层正则化。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import sys, os
hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)
from PYTORCH.Deep_eye.Pytorch_Camp_master.hello_pytorch.tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter
# set_seed(1) # 设置随机种子
class Net(nn.Module):
def __init__(self, neural_num, d_prob=0.5):
super(Net, self).__init__()
self.linears = nn.Sequential(
nn.Dropout(d_prob),
nn.Linear(neural_num, 1, bias=False),
nn.ReLU(inplace=True)
)
def forward(self, x):
return self.linears(x)
input_num = 10000
x = torch.ones((input_num, ), dtype=torch.float32)
net = Net(input_num, d_prob=0.5)
net.linears[1].weight.detach().fill_(1.)
net.train()
y = net(x)
print("output in training mode", y)
net.eval()
y = net(x)
print("output in eval mode", y)
OUT:
output in training mode tensor([9982.], grad_fn=<ReluBackward0>)
output in eval mode tensor([10000.], grad_fn=<ReluBackward0>)
注意: Keras中Dropout的实现,是屏蔽掉某些神经元,使其激活值为0以后,对激活值向量x1……x1000进行放大,也就是乘以1/(1-p)。
思考:
上面我们介绍了两种方法进行Dropout的缩放,那么Dropout为什么需要进行缩放呢?
因为我们训练的时候会随机的丢弃一些神经元,但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元,这会带来结果不稳定的问题,也就是给定一个测试数据,有时候输出a有时候输出b,结果不稳定,这是实际系统不能接受的,用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个p,这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是x,那么在训练的时候它有p的概率参与训练,(1-p)的概率丢弃,那么它输出的期望是px+(1-p)0=px。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望。
总结:
当前Dropout被大量利用于全连接网络,而且一般认为设置为0.5或者0.3,而在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积网络隐藏层中使用较少。总体而言,Dropout是一个超参,需要根据具体的网络、具体的应用领域进行尝试。