【路径规划】蚁群算法求解两点最短路径matlab

1.关于旅行商(TSP)问题及衍化

　　旅行商问题(Traveling Saleman Problem，TSP)是车辆路径调度问题(VRP)的特例，由于数学家已证明TSP问题是NP难题，因此，VRP也属于NP难题。旅行商问题(TSP)又译为旅行推销员问题、货郎担问题，简称为TSP问题，是最基本的路线问题，该问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本。——旅行商问题百科

　　很明显，当节点数很少时，大多数人都会想到，问题很简单，直接穷举就OK了，但实际问题中，节点数往往很大，变得不可能。例如：对于一个仅有16个城市的旅行商问题，如果用穷举法来求问题的最优解，需比较的可行解有：15!/2=653，837，184，000个。在1993年，使用当时的工作站用穷举法求解此问题需时92小时。即使现在计算机速度快，但是面对复杂的问题，仍然不够。这就是所谓的“组合爆炸”，指数级的增长，所以科学家逐步寻找近似算法或者启发式算法，目的是在合理的时间范围内找到可接受的最优解。

　　TSP问题解决算法的发展可以分为3个部分：

1).经典精确算法:穷举法、线性规划算法、动态规划算法、分支定界算法等运筹学中的传统算法，这些算法复杂度一般都很大，只适用于求解小规模问题。

2).近似算法：当问题规模较大时，其所需的时间成级数增长，这是我们无法接受的，算法求解问题的规模受到了很大的限制，一个很自然的想法就是牺牲精确解法中的最优性，去寻找一个好的时间复杂度我们可以容忍的，同时解的质量我们可以接受的算法．基于这一思想所设计出的算法统称为近似算法。如插入算法，最邻近算法等。

3).智能算法：随着科学技术和生产的不断发展，许多实际问题不可能在合理的时间范围内找到全局最优解，这就促使了近代最优化问题求解方法的产生。随着各种不同搜索机制的启发式算法相继出现，如禁忌搜索、遗传算法、模拟退火算法、人工神经网络、进化策略、进化编程、粒子群优化算法、蚁群优化算法和免疫计算等，掀起了研究启发式算法的高潮。

　　具体每一种算法不再详细描述，大家可以针对性的寻找相应资料进行了解。

　　TSP问题在实际的生产生活中，更加实际环境不同，有很多衍生的经典问题。车辆路径调度(VRP)扩展问题是经典VRP加入各种约束条件后而形成的。例如需求约束形成的需求随机的车辆路径问题(SVRP);加入时间约束得到的带时间窗的车辆路径题(VRPTW);加入距离约束的距离约束车辆路径问题(DVRP);根据其它条件的不同,还有多配送中心车辆路径问题(MDVRP)、可切分的车辆路径问题(SDVRP);先配送再收集车辆路径问题(VRPB)、配送收集车辆路径问题(VRPPD);信息不完全的模糊车辆路径问题(FVRP)[3]。

回到目录

2.群蚁算法基本原理

2.1 算法综述

　　对于VRP问题,求解算法大致可分为精确算法和人工智能算法两大类。精确性算法基于严格的数学手段,在可以求解的情况下,解的质量较好。但是由于算法严格,运算量大,特别是大规模的问题几乎无法求解。所以其应用只能是小规模的确定性问题，面对中小规模问题,人工智能算法在精度上不占优势。但规模变大时,人工智能方法基本能在可接受时间里,找到可接受的满意解,这是精确算法难以做到的。由于的实际问题,各种约束错综复杂,人工智能算法显示出了巨大的优越性,也正因为如此,实际应用中,人工智能算法要更广泛。求解车辆路径调度问题的精确算法有动态规划法、分枝定界法等。并开始寻求所得结果可接受的启发式算法,以处理大规模实际问题，一些其他学科的新一代优化算法相继出现,如禁忌搜索算法,遗传算法,人工神经网络算法,以及现在研究较多的蚁群算法等。

2.2 群蚁算法的原理

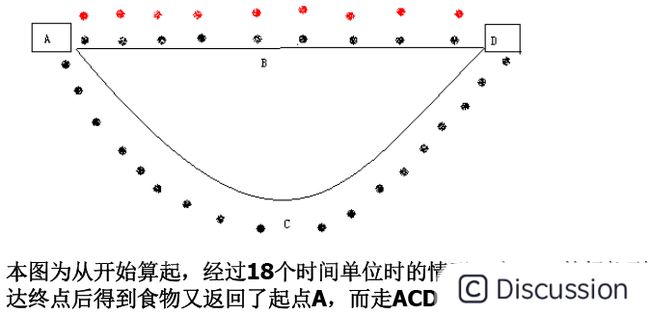
　　蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明：一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。蚂蚁在运动时能够感知这种物质,并且习惯于追踪此物质爬行,当然爬行过程中还会释放信息素。一条路上的信息素踪迹越浓,其它蚂蚁将以越高的概率跟随爬行此路径,从而该路径上的信息素踪迹会被加强,因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越大。蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标的。我们举例简单说明蚂蚁觅食行为：

    

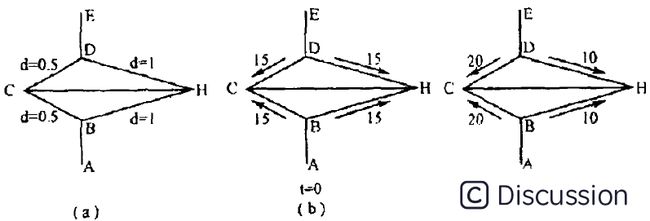
    如上图a,b,c的示意图：

    a图是原始状态，蚂蚁起始点为A，要到达E，中途有障碍物，要绕过才能到达。BC和BH是绕过障碍物的2条路径(假设只有2条)。各个路径的距离d已经标定。

    b图是t=0时刻蚂蚁状态，各个边上有相等的信息素浓度，假设为15；

    c图是t=1时刻蚂蚁经过后的状态，各个边的信息素浓度，有变化；因为大量蚂蚁的选择概率会不一样，而选择概率是和路径长度相关的。所以越短路径的浓度会越来越大，经过此短路径达到目的地的蚂蚁也会比其他路径多。这样大量的蚂蚁实践之后就找到了最短路径。所以这个过程本质可以概括为以下几点：

    1.路径概率选择机制信息素踪迹越浓的路径,被选中的概率越大

    2.信息素更新机制路径越短,路径上的信息素踪迹增长得越快

    3.协同工作机制蚂蚁个体通过信息素进行信息交流。

    从蚂蚁觅食的原理可见,单个个体的行为非常简单蚂蚁只知道跟踪信息素爬行并释放信息素,但组合后的群体智能又非常高蚂蚁群能在复杂的地理分布的清况下,轻松找到蚁穴与食物源之间的最短路径。这种特点恰恰与元启发算法的特点相一致,蚁群优化算法正是受到这种生态学现象的启发后加以模仿并改进而来,觅食的蚂蚁由人工蚁替代,蚂蚁释放的信息素变成了人工信息素,蚂蚁爬行和信息素的蒸发不再是连续不断的,而是在离散的时空中进行。

　　上述例子如果不好理解，我在这里贴几张PPT，个人感觉非常不错，也是我找了很多资料觉得最好理解的【来源是大连理工大学谷俊峰】，点击这里提供下载：蚁群算法基本知识.rar。

    从深层意义上来讲,蚁群算法作为优化的方法之一,属于人工群集智能领域。人工群集智能,大都受自然群集智能如昆虫群和动物群等的启发而来。除了具有独特的强有力的合作搜索能力外,还可以利用一系列的计算代理对问题进行分布式处理,从而大大提高搜索效率。

回到目录

3.群蚁算法的基本流程

　　我们还是采用大连理工大学谷俊峰的PPT来说明问题，重要公式进行截图计算和解释，对PPT难以理解的地方进行单独解释：

3.1 基本数学模型

　　首先看看基本TSP问题的基本数学模型：

　　问题其实很简单，目标函数就是各个走过路径的总长度，注意的就是距离矩阵根据实际的问题不一样，长度是不一样的。

3.2 群蚁算法说明

　　在说明群蚁算法流程之前，我们对算法原理和几个注意点进行描述：

1.TSP问题的人工蚁群算法中，假设m只蚂蚁在图的相邻节点间移动，从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定：1. 信息素值也称信息素痕迹。2.可见度，即先验值。\ 2.信息素的更新方式有2种，一是挥发，也就是所有路径上的信息素以一定的比率进行减少，模拟自然蚁群的信息素随时间挥发的过程；二是增强，给评价值“好”(有蚂蚁走过)的边增加信息素。\ 3.蚂蚁向下一个目标的运动是通过一个随机原则来实现的，也就是运用当前所在节点存储的信息，计算出下一步可达节点的概率，并按此概率实现一步移动，逐此往复，越来越接近最优解。\ 4.蚂蚁在寻找过程中，或者找到一个解后，会评估该解或解的一部分的优化程度，并把评价信息保存在相关连接的信息素中。 

3.3 群蚁算法核心步骤

　　更加我们前面的原理和上述说明，群蚁算法的2个核心步骤是 路径构建 和 信息素更新。我们将重点对这2个步骤进行说明。

3.3.1 路径构建

　　每个蚂蚁都随机选择一个城市作为其出发城市，并维护一个路径记忆向量，用来存放该蚂蚁依次经过的城市。蚂蚁在构建路径的每一步中，按照一个随机比例规则选 择下一个要到达的城市。随机概率是按照下列公式来进行计算的：

　　上述公式就是计算 当前点 到 每一个可能的下一个节点 的概率。分子是 信息素强度 和 能见度 的幂乘积，而分母则是所有 分子的和值。这个刚开始是很不容易理解的，我们在最后实例计算的时候，可以看得很清楚，再反过来理解公式。注意每次选择好节点后，就要从可用节点中移除选择的节点。

3.3.2 信息素更新

　　信息素更新是群蚁算法的核心。也是整个算法的核心所在。算法在初始期间有一个固定的浓度值，在每一次迭代完成之后，所有出去的蚂蚁回来后，会对所走过的路线进行计算，然后更新相应的边的信息素浓度。很明显，这个数值肯定是和蚂蚁所走的长度有关系的，经过一次次的迭代， 近距离的线路的浓度会很高，从而得到近似最优解。那我们看看信息素更新的过程。

　　初始化信息素浓度C(0)，如果太小，算法容易早熟，蚂蚁会很快集中到一条局部最优路径上来，因为可以想想，太小C值，使得和每次挥发和增强的值都差不多，那么 随机情况下，一些小概率的事件发生就会增加非最优路径的信息素浓度；如果C太大，信息素对搜索方向的指导性作用减低，影响算法性能。一般情况下，我们可以使用贪婪算法获取一个路径值Cnn，然后根据蚂蚁个数来计算C(0) = m/Cnn ,m为蚂蚁个数

　　每一轮过后，问题空间中的所有路径上的信息素都会发生蒸发,然后，所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素，公式如下： 

　　信息素更新的作用：\ 1.信息素挥发(evaporation)信息素痕迹的挥发过程是每个连接上的 信息素痕迹的浓度自动逐渐减弱的过程，这个挥发过程主要用于避 免算法过快地向局部最优区域集中，有助于搜索区域的扩展。\ 2.信息素增强(reinforcement)增强过程是蚁群优化算法中可选的部 分，称为离线更新方式(还有在线更新方式)。这种方式可以实现 由单个蚂蚁无法实现的集中行动。基本蚁群算法的离线更新方式是 在蚁群中的m只蚂蚁全部完成n城市的访问后，统一对残留信息进行 更新处理。

3.3.3 迭代与停止

　　迭代停止的条件可以选择合适的迭代次数后停止，输出最优路径，也可以看是否满足指定最优条件，找到满足的解后停止。最重要的是，我刚开始理解这个算法的时候，以为每一只蚂蚁走一条边就是一次迭代，其实是错的。这里算法每一次迭代的意义是：每次迭代的m只蚂蚁都完成了自己的路径过程，回到原点后的整个过程。

回到目录

4.群蚁算法计算实例

　　使用PPT中的一个案例，非常直观，对几个符号错误进行了修改，主要是计算概率的乘号，结果没有错误：

　　过程总体还是比较简单的，注意理解公式，然后把公式和实例结合起来看，最好是拿笔自己手动画一画，容易理解。下面我们来看看如何编程实现TSP问题的群蚁算法代码。

``` % Ant main program

clear all; close all; clc;

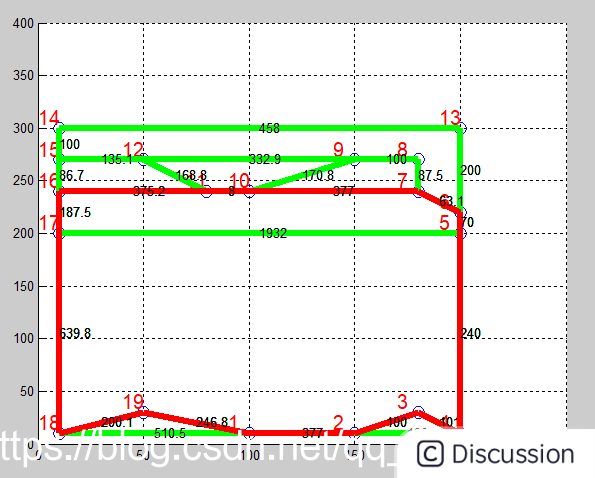
tic; Ant=25;%蚂蚁数量 Ger=120;%迭代次数 firstaddress = [ 100,10 150,10 180,30 200,10 200,200 200,220 180,240 180,270 150,270 100,240 80,240 50,270 200,300 10,300 10,270 10,240 10,200 10,10 50,30 100,10 ];%firstaddress表示测试数据中的节点坐标

SumOfCity = size(firstaddress,1);%节点个数 lengthaddress =10000.*ones(SumOfCity,SumOfCity);%lengthaddress表示两两节点间的距离，初始设定10000，可以设定无穷大，表示不相连 lengthaddress(1,2)=377;%表示节点1和节点2的距离 lengthaddress(2,4)=190; lengthaddress(2,3)=100; lengthaddress(3,4)=101; lengthaddress(4,5)=240; lengthaddress(5,17)=1932; lengthaddress(5,6)=70; lengthaddress(6,13)=200; lengthaddress(6,7)=63.1;

lengthaddress(7,10)=377; lengthaddress(7,8)=87.5; lengthaddress(8,9)=100; lengthaddress(10,11)=8; lengthaddress(9,10)=170.8; lengthaddress(9,12)=332.9; lengthaddress(11,12)=168.8; lengthaddress(11,16)=375.2; length_address(12,15)=135.1;

lengthaddress(13,14)=458; lengthaddress(14,15)=100; lengthaddress(15,16)=86.7; lengthaddress(16,17)=187.5; length_address(17,18)=639.8;

lengthaddress(18,20)=510.5; lengthaddress(18,19)=200.1; lengthaddress(19,20)=246.8; for n=1:size(firstaddress) for m=1:size(firstaddress) if lengthaddress(n,m)~=10000 lengthaddress(m,n)=lengthaddress(n,m); %对称矩阵 end end end

power=lengthaddress;%距离 [PM PN]=size(power);%距离矩阵大小，行列个数 % %% 画出节点分布图形 % figure(1); % grid on; % hold on; % scatter(firstaddress(:,1),firstaddress(:,2)); % for i=1:PN % for j=1:PN % if(lengthaddress(i,j)~=10000) % line([firstaddress(i,1),firstaddress(j,1)],[firstaddress(i,2),firstaddress(j,2)],'Color','g');%划线 % text((firstaddress(i,1)+firstaddress(j,1))/2,(firstaddress(i,2)+firstaddress(j,2))/2,num2str(length_address(i,j)));%标注线段距离 % end % end % end

% 初始化蚂蚁位置 v=init_population(Ant,PN); v(:,1)=1;%起点 v(:,PN)=1;%终点

fit=shortroadfun(v,power);%求每条路径的距离 T0 = max(fit)-fit;

% 初始化 vmfit=[]; vx=[]; P0=0.2; % P0----全局转移选择因子 P=0.8; % P ----信息素蒸发系数 %C=[]; % 开始寻优 for iger=1:Ger lamda=1/iger; % 转移步长参数 [TBest(iger),BestIndex]=max(T0); for jg=1:Ant % 求取全局转移概率 r=T0(BestIndex)-T0(jg); Prob(iger,jg)=r/T0(BestIndex); end %对100只蚂蚁进行路径的转变 for jgtr=1:Ant %路径进行改变，该路径存放到temp变量，1表示经过该列所在的节点数 if Prob(iger,jgtr) g tr,:)-2.*(v(jg tr,:).*M)+M; else M=rand(1,PN) g tr,:)-2.*(v(jg tr,:).*M)+M; end temp(:,1)=1;%起点和终点必须有蚂蚁存在 temp(:,end)=1; %判转变后的临时路径距离是否小于原来的路径，是的话就将该蚂蚁的路径进行转换成temp中存放的路径 if shortroad fun(temp,power) road fun(v(jg tr,:),power) v(jg_tr,:)=temp; end end

%信息素更新

   [sol,indb]=min(fit);
v(1,:)=v(indb,:);%第一只蚂蚁的路径保存最小路径
media=mean(fit);
vx=[vx sol];%存放每一代最小的距离
%     vmfit=[vmfit media];

end

% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % %%%% 最后结果 % 显示最优解及最优值 % v(indb,:) disp(sprintf('Code of shortroad is: %s',num2str(v(indb,:)))); disp(sprintf('\n')); %空一行 disp(sprintf('Shortroad is: %s',num2str(find(v(indb,:))))); disp(sprintf('Mininum is: %d',sol)); route=find(v(indb,:)); % 画出节点分布图形 figure(2); grid on; hold on; for i=1:PN-1 plot(firstaddress(i,1),firstaddress(i,2),'bo','MarkerSize',10); str=num2str(i); text(firstaddress(i,1)-10,firstaddress(i,2)+10,str,'Color','red','FontSize',15); end m=length(route); for i=1:m plot(firstaddress(route(i),1),firstaddress(route(i),2),'MarkerSize',10,'MarkerEdgeColor','k','MarkerFaceColor',[0.5,0.5,0.5]) ; hold on; end for i=1:PN for j=1:PN if(lengthaddress(i,j)~=10000) line([firstaddress(i,1),firstaddress(j,1)],[firstaddress(i,2),firstaddress(j,2)],'Color','g','LineWidth',5);%划线 text((firstaddress(i,1)+firstaddress(j,1))/2,(firstaddress(i,2)+firstaddress(j,2))/2,num2str(lengthaddress(i,j)));%标注线段距离 end end end %% 最短路径 for p=1:m-1 if(route(p+1)~=20) line([firstaddress(route(p),1),firstaddress(route(p+1),1)],[firstaddress(route(p),2),firstaddress(route(p+1),2)],'Color','r','LineWidth',5);%划线 text((firstaddress(route(p),1)+firstaddress(route(p+1),1))/2,(firstaddress(route(p),2)+firstaddress(route(p+1),2))/2,num2str(lengthaddress(route(p),route(p+1))));%标注线段距离 else line([firstaddress(route(p),1),firstaddress(1,1)],[firstaddress(route(p),2),firstaddress(1,2)],'Color','r','LineWidth',5);%划线 text((firstaddress(route(p),1)+firstaddress(1,1))/2,(firstaddress(route(p),2)+firstaddress(1,2))/2,num2str(lengthaddress(route(p),route(p+1))));%标注线段距离 end end axis([0 250 0 400]) % 图形显示最优及平均函数值变化趋势 % figure(3); % plot(vx); % title('最优,平均函数值变化趋势'); % xlabel('Generations'); % ylabel('f(x)'); % hold on; % plot(vmfit,'r'); % hold off;

runtime=toc ```