红黑树插入实现(java)
文章目录
-
- 红黑树的定义与性质
- LL类型的右旋
- RR类型的左旋
- 插入
-
- 插入平衡性逻辑
- 插入图解
- 插入代码
- 平衡性代码
- 删除
- 代码实现
红黑树的定义与性质
红黑树是一种含红节点和黑节点并且能够自平衡的二叉树
-
节点颜色不是红色就是黑色
-
根节点是黑色
-
叶子节点(为null叶子节点)都是黑色
-
如果一个节点的颜色是红色,它的子节点一定是黑色
-
任意一节点到每个叶子节点的路径都包含数量相同的黑节点
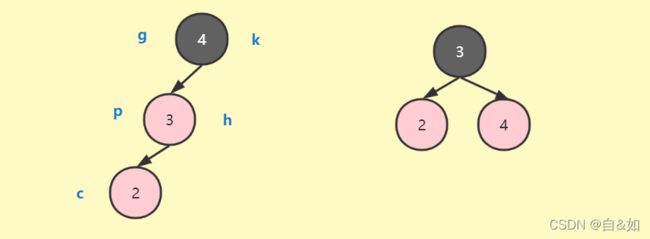
LL类型的右旋
-
这里的左旋和右旋的代码和avl树有些不一样,需要考虑节点类的父节点
-
g或者p当作k参数传入右旋方法
LL
public void rotateR(Node k){
Node h = k.left;
k.left = h.right;
if(h.right != null){
h.right.parent = k;
}
if(k.parent == null){
root = h;
}else{
if(k.parent.right == k){
k.parent.right = h;
}else{
k.parent.left = h;
}
}
h.right = k;
k.parent = h;
}
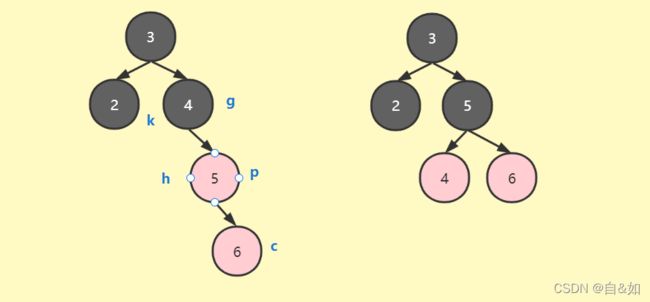
RR类型的左旋
-
这里的左旋和右旋的代码和avl树有些不一样,需要考虑节点类的父节点
-
g或者p当作k参数传入右旋方法
RR类型左旋
public void rotateL(Node k){
Node h = k.right;
k.right = h.left;
if(h.left != null){
h.left.parent = k;
}
h.parent = k.parent;
if(k.parent == null){
root = h;
}else{
if(k.parent.left == k){
k.parent.left = h;
}else{
k.parent.right = h;
}
}
h.left = k;
k.parent = h;
}
插入
插入平衡性逻辑
- 默认插入的节点的颜色为红色
1、直接插入,改变根节点颜色
2、父节点为黑色,直接插入
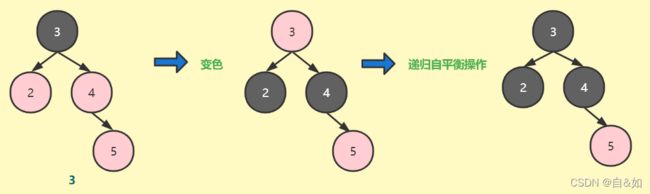
3、插入节点父节点和叔叔节点都为红色,变色(父节点和叔叔节点变黑,爷爷变红), 爷爷节点传入执行递归的平衡方法
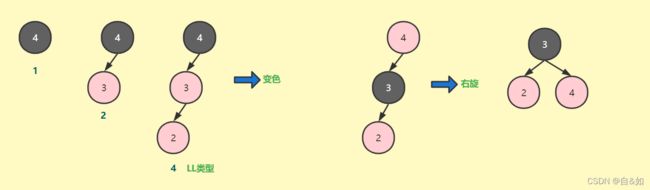
4、插入节点的父节点为红色并且是父节点的左子树,叔叔节点为空或者黑色,并且父节点是爷爷节点的左子树,相当于avl树LL类型,先变色(父节点变黑,爷爷变红),然后右旋
5、插入节点的父节点为红色并且是父节点的左子树,叔叔节点为空或者黑色,并且父节点是爷爷节点的左子树,相当于avl树的LR类型,插入节点的父节点先左旋,传入父节点在执行递归执行平衡性函数
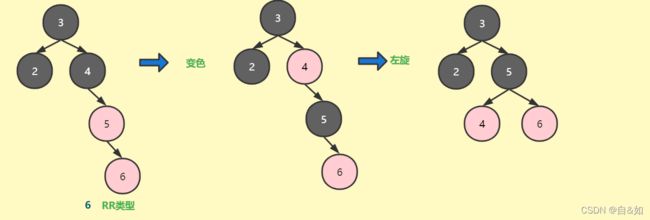
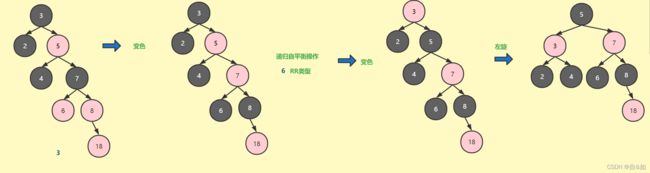
6、插入的节点的父节点为红色并且是父节点的右子树,叔叔节点为黑色或者为空,并且父节点是爷爷节点的右子树,相当于avl树的RR类型,先变色(父节点变黑,爷爷变红),然后左旋
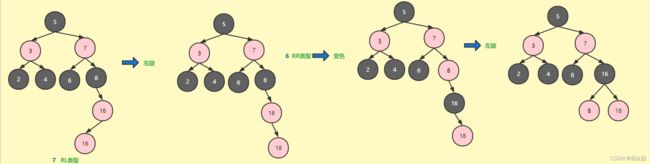
7、插入的节点的父节点为红色并且是父节点的左子树,叔叔节点为黑色或者为空,并且父节点是爷爷节点的右子树,相当于avl树的RL类型,插入节点的父节点先右旋,传入父节点在执行递归执行平衡性函数
private void balance(Node node){
root.color = BLACK;
Node parent = parent(node);
Node grandpa = parent(parent);
//父节点红红色
if(parent!=null && isRed(parent)){
Node uncle = null;
//父节点为爷爷的左子树
if(parent == grandpa.left){
uncle = grandpa.right;
//父节点和叔叔节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者为黑色
if (uncle == null || isBlack(uncle)) {
//插入的节点为父节点的左子树LL
if(node == parent.left){
parent.color = BLACK;
grandpa.color = RED;
rotateR(grandpa);
return;
}
//插入的节点为父节点的右子树LR
if(node == parent.right){
rotateL(parent);
balance(parent);
return;
}
}
}else{
//父节点为爷爷节点的右子树
uncle = grandpa.left;
//叔叔节点和父节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者黑色
if(uncle == null || isBlack(uncle)){
//插入的节点为父节点的右子树
if(node == parent.right){
parent.color = BLACK;
grandpa.color = RED;
rotateL(grandpa);
return;
}
//插入的节点为父节点的左子树
if(node == parent.left){
rotateR(parent);
balance(grandpa);
return;
}
}
}
}
}
插入图解
插入代码
public void put(K key,V val){
Node parent = null;
Node curr = root;
while(curr!=null){
parent = curr;
int cmp = key.compareTo((K)curr.key);
if(cmp>0){
curr = curr.right;
}else if(cmp<0){
curr = curr.left;
}else{
curr.val = val;
return;
}
}
Node newNode = new Node(key,val,parent,null,null,RED);
if(parent!=null){
int cmp = key.compareTo((K)parent.key);
if(cmp>0){
parent.right = newNode;
this.len++;
balance(newNode);
return;
}else{
parent.left = newNode;
this.len++;
balance(newNode);
return;
}
}else{
root = newNode;
this.len++;
return;
}
}
平衡性代码
- 每一次插入操作都需左平衡性操作
private void balance(Node node){
root.color = BLACK;
Node parent = parent(node);
Node grandpa = parent(parent);
//父节点红红色
if(parent!=null && isRed(parent)){
Node uncle = null;
//父节点为爷爷的左子树
if(parent == grandpa.left){
uncle = grandpa.right;
//父节点和叔叔节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者为黑色
if (uncle == null || isBlack(uncle)) {
//插入的节点为父节点的左子树LL
if(node == parent.left){
parent.color = BLACK;
grandpa.color = RED;
rotateR(grandpa);
return;
}
//插入的节点为父节点的右子树LR
if(node == parent.right){
rotateL(parent);
balance(parent);
return;
}
}
}else{
//父节点为爷爷节点的右子树
uncle = grandpa.left;
//叔叔节点和父节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者黑色
if(uncle == null || isBlack(uncle)){
//插入的节点为父节点的右子树
if(node == parent.right){
parent.color = BLACK;
grandpa.color = RED;
rotateL(grandpa);
return;
}
//插入的节点为父节点的左子树
if(node == parent.left){
rotateR(parent);
balance(grandpa);
return;
}
}
}
}
}
删除
- 删除本身不难,和二叉树删除一样,但是要考虑节点颜色问题,这个逻辑挺复杂,这里就先不实现了
代码实现
------------红黑树元素个数测试:---------------
6
------------红黑树深度测试:------------------
4
-------------中序遍历:--------------------
-----红节点颜色为true,黑节点颜色为false:------
key:2---color:false---val:2
key:3---color:false---val:3
key:4---color:false---val:4
key:5---color:true---val:5
key:6---color:false---val:6
key:7---color:true---val:7
测试
import java.util.ArrayList;
public class RBTreeTest {
public static void main(String[] args) {
RBTree<Integer,String> tree = new RBTree<>();
tree.put(4, "s");
tree.put(3, "t");
tree.put(2, "r");
tree.put(5, "z");
tree.put(6, "a");
tree.put(7, "q");
System.out.println("------------红黑树元素个数测试:---------------");
System.out.println(tree.size());
System.out.println("------------红黑树深度测试:------------------");
System.out.println(tree.height());
System.out.println("-------------中序遍历:--------------------");
System.out.println("-----红节点颜色为true,黑节点颜色为false:------");
ArrayList<Integer> keys = tree.middlebl();
for (Object key : keys) {
Integer val = tree.get((Integer) key);
RBTree.Node node = tree.get(tree.root, (Integer) key);
boolean color = node.isColor();
System.out.println("key:"+key + "---color:" +color + "---val:"+val);
}
}
}
代码实现
import java.util.ArrayList;
import java.util.LinkedList;
public class RBTree<K extends Comparable<K>,V> {
Node root;
int len;
private static final boolean RED = true;
private static final boolean BLACK = false;
RBTree(){
root = null;
this.len = 0;
}
public int size(){
return this.len;
}
public boolean isRed(Node node){
if(node == null){
return false;
}
return node.color == RED;
}
public boolean isBlack(Node node){
if(node == null){
return false;
}
return node.color == BLACK;
}
public Node parent(Node node){
if(node!=null){
return node.parent;
}
return null;
}
public void rotateL(Node k){
Node h = k.right;
k.right = h.left;
if(h.left != null){
h.left.parent = k;
}
h.parent = k.parent;
if(k.parent == null){
root = h;
}else{
if(k.parent.left == k){
k.parent.left = h;
}else{
k.parent.right = h;
}
}
h.left = k;
k.parent = h;
}
public void rotateR(Node k){
Node h = k.left;
k.left = h.right;
if(h.right != null){
h.right.parent = k;
}
if(k.parent == null){
root = h;
}else{
if(k.parent.right == k){
k.parent.right = h;
}else{
k.parent.left = h;
}
}
h.right = k;
k.parent = h;
}
public void put(K key,V val){
Node parent = null;
Node curr = root;
while(curr!=null){
parent = curr;
int cmp = key.compareTo((K)curr.key);
if(cmp>0){
curr = curr.right;
}else if(cmp<0){
curr = curr.left;
}else{
curr.val = val;
return;
}
}
Node newNode = new Node(key,val,parent,null,null,RED);
if(parent!=null){
int cmp = key.compareTo((K)parent.key);
if(cmp>0){
parent.right = newNode;
this.len++;
balance(newNode);
return;
}else{
parent.left = newNode;
this.len++;
balance(newNode);
return;
}
}else{
root = newNode;
this.len++;
return;
}
}
private void balance(Node node){
root.color = BLACK;
Node parent = parent(node);
Node grandpa = parent(parent);
//父节点红红色
if(parent!=null && isRed(parent)){
Node uncle = null;
//父节点为爷爷的左子树
if(parent == grandpa.left){
uncle = grandpa.right;
//父节点和叔叔节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者为黑色
if (uncle == null || isBlack(uncle)) {
//插入的节点为父节点的左子树LL
if(node == parent.left){
parent.color = BLACK;
grandpa.color = RED;
rotateR(grandpa);
return;
}
//插入的节点为父节点的右子树LR
if(node == parent.right){
rotateL(parent);
balance(parent);
return;
}
}
}else{
//父节点为爷爷节点的右子树
uncle = grandpa.left;
//叔叔节点和父节点为红色
if(uncle!=null && isRed(uncle)){
parent.color = BLACK;
uncle.color = BLACK;
grandpa.color = RED;
balance(grandpa);
return;
}
//叔叔节点为空或者黑色
if(uncle == null || isBlack(uncle)){
//插入的节点为父节点的右子树
if(node == parent.right){
parent.color = BLACK;
grandpa.color = RED;
rotateL(grandpa);
return;
}
//插入的节点为父节点的左子树
if(node == parent.left){
rotateR(parent);
balance(grandpa);
return;
}
}
}
}
}
public K get(K key){
return (K) get(root,key).key;
}
public Node get(Node node, K key){
if(node == null){
return null;
}
int cmp = key.compareTo((K)node.key);
if(cmp>0){
return get(node.right,key);
}else if(cmp<0){
return get(node.left,key);
}else{
return node;
}
}
public ArrayList<K> middlebl(){
if(root == null){
return null;
}
ArrayList<K> keys = new ArrayList<>();
LinkedList<Node> stack = new LinkedList<>();
Node temp = root;
while(temp!=null || !stack.isEmpty()){
while(temp!=null){
stack.addFirst(temp);
temp = temp.left;
}
temp = stack.removeFirst();
keys.add((K)temp.key);
temp = temp.right;
}
return keys;
}
public int height(){
return height(root);
}
private int height(Node node){
if(node == null){
return 0;
}
int maxl = 0;
int maxr = 0;
int max = 0;
maxl = height(node.left);
maxr = height(node.right);
max = Math.max(maxl,maxr)+1;
return max;
}
class Node<K extends Comparable<K>,V> {
K key;
V val;
Node parent;
Node left;
Node right;
boolean color;
Node(){}
public Node(K key, V val, Node parent, Node left, Node right, boolean color) {
this.key = key;
this.val = val;
this.parent = parent;
this.left = left;
this.right = right;
this.color = color;
}
public String toString() {
return ""+key+(this.color==RED?"(R)":"B");
}
public K getKey() {
return key;
}
public V getVal() {
return val;
}
public Node getParent() {
return parent;
}
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
public boolean isColor() {
return color;
}
public void setKey(K key) {
this.key = key;
}
public void setVal(V val) {
this.val = val;
}
public void setParent(Node parent) {
this.parent = parent;
}
public void setLeft(Node left) {
this.left = left;
}
public void setRight(Node right) {
this.right = right;
}
public void setColor(boolean color) {
this.color = color;
}
}
}