第八个模型:神经网络学习(深度学习)模型
=======================================================================
Machine Learning notebook
Python机器学习基础教程(introduction to Machine Learning with Python)
=======================================================================
神经网络(深度学习)
一类被称为神经网络的算法最近以“深度学习”的名字再度流行。虽然深度学习在许多机器学习应用中都有巨大的潜力,但深度学习算法往往经过精确调整,只适用于特定的使用场景。这里只讨论一些相对简单的方法,即用于分类和回归的多层感知机(multilayer perceptron,MLP),它可以作为研究更复杂的深度学习方法的起点。MLP也被称为(普通)前馈神经网络,有时也简称神经网络。
1、神经网络模型
MLP可以被视为广义的线性模型,执行多层处理后得到结论。
线性回归的预测公式为:
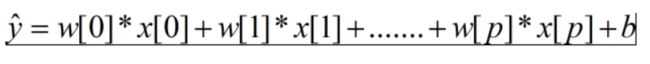
y是输入特征x[0]到x[p]的加权求和,权重为学到的系数w[0]到w[p]。
将这个公式可视化后可得到:
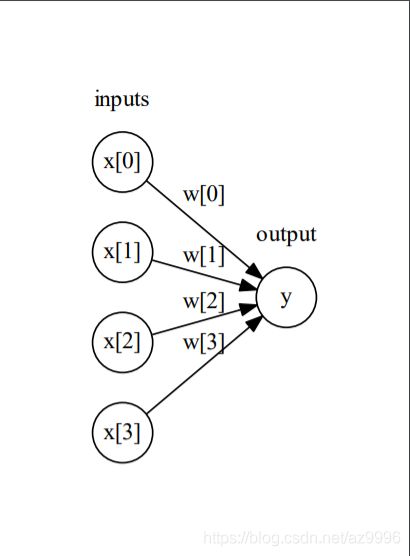
左边的每个结点代表一个输入特征,连线代表学到的系数,右边的结点代表输出,是输入的加权求和。
在MLP中,多次重复这个计算加权求和的过程,首先计算代表中间过程的隐单元(hidden unit),然后再计算这些隐单元的加权求和并得到最终结果。
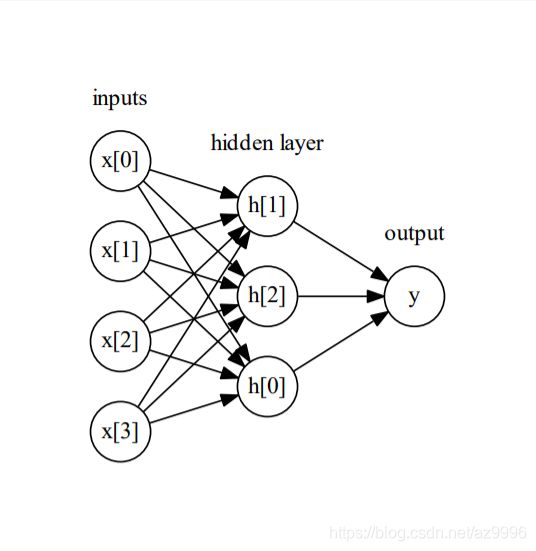
这个模型需要学习更多的系数(也叫做权重):在每个输入与每个隐单元(隐单元组成了隐层)之间有一个系数,在每个隐单元与输出之间也有一个系数。
从数学角度看,计算一系列加权求和与只计算一个加权求和是完全相同的,因此,为了让这个模型真正比线性模型更为强大,我们还需要一个技巧。在计算完每个隐单元的加权求和之后,对结果再应用一个非线性函数——通常是校正非线性(rectify nonlinearity,也叫校正线性单元或relu)或正切双曲线(tangens hyperbolicus,tanh)。然后将这个函数的结果用于加权求和,计算的到输出y。
relu截断小于0的值,而tanh在输入值较小时接近-1,在输入值较大时接近+1.有了这两种非线性函数,神经网络可以学习比线性模型复杂得多的函数。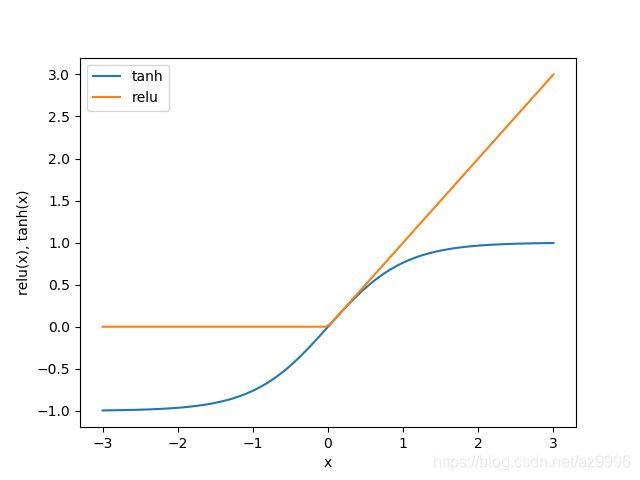

w是输入x与隐层h之间的权重,v是隐层h与输出y之间的权重。权重w和v要从数据中学到,x是输入特征,y是计算的到的输出,h是计算的中间结果。需要用户设置的一个重要参数是隐层中的结点个数。对于非常小或非常简单的数据集,这个值可以小到10;对于非常复杂的数据,这个值可以扩大到10000。也可以添加多个隐层。
这些由许多计算层组成的大型神经网络,正是术语“深度学习”的灵感来源。
2、神经网络调参
神经网络学到的决策边界完全是非线性的,但相对平滑。
默认情况下,MLP使用100个隐结点,这对于小型数据集来说已经相当多了。
默认的非线性函数时relu。
若果想得到更加平滑的决策边界,可以添加更多的隐单元、添加第二个隐层或者使用tanh非线性函数。
我们还可以利用L2惩罚使权重趋向于0,从而控制神经网络的复杂度,正如我们在岭回归和线性分类器中所作的那样。MLPclassifier中调节L2惩罚的参数alpha(与线性回归模型中的相同),它的默认值很小(弱正则化)。
神经网络的一个重要性质:在开始学习之前权重是随机设置的,这种随机初始化会影响学到的模型。也就是说,即使使用完全相同的参数,如果随机种子不同的话,我们也可能得到非常不一样的模型。如果网络很大,并且复杂度选择合理的话,那么这应该不会对精度有太大影响,但应该记住这一点(特别是对于较小的网络)。
神经网络也要求所有输入特征的变化范围相似,最理想的情况是均值为0、方差为1.我们必须对数据进行缩放以满足这些要求。StandardScaler方法可自动对数据进行预处理。
alpha参数的范围(从0.0001到1),alpha越大代表更强的正则化。
虽然不可以分析神经网络学到了什么,但这通常比分析线性模型或基于树的模型更为复杂。要想观察模型学到了什么,一种方法是查看模型的权重。示例:https://scikit-learn.org/stable/auto_examples/neural_networks/plot_mnist_filters.html
行对应30个输入特征,列对应100个隐单元。浅色代表较大的正值,而深色代表负值。
我们可以推断,如果某个特征对所有隐单元的权重都很小,那么这个特征对模型来说就“不太重要”。
还可以将连接隐层和输出层的权重可视化,但它们更加难以解释。
比scikit-learn库使用更灵活或更大的模型库(深度学习库) Keras、lasagna、tensor-flow。
lasagna是基于theano库构建的,而Keras既可以用tensor-flow也可以用theano。这些库提供了更为灵活的接口,可以用来构建神经网络并跟踪深度学习研究的快速发展。所有流行的深度学习库也都允许使用高性能的图形处理单元(GPU),而scikit-learn不支持GPU。
3、优点、缺点和参数
在机器学习的许多应用中,神经网络再次成为最先进的模型。它的注意优点之一是能够获取大量数据中包含的信息,并构建无比复杂的模型。给定足够的计算时间和数据,并且自习调节参数,神经网络通常可以打败其它机器学习算法(无论是分类任务还是回归任务)。
缺点
神经网络——特别是功能强大的大型神经网络——通常需要很长的训练时间。它还需要仔细的预处理数据,正如我们这里所看到的。与SVM类似,神经网络在“均匀”数据上的性能最好,其中“均匀”是指所有特征都具有相似的含义。如果数据包含不同种类的特征,那么基于树的模型的可能表现的更好。神经网络调参是一门艺术。
估计神经网络的复杂度 最重要的参数是层数和每层的隐单元个数。你应该首先设置1个或2个隐层,然后可以逐步增加。每个隐层的结点个数通常与输入特征个数接近,但在几千个结点时很少会多于特征个数。
一个有用的度量是学到的权重(或系数)的个数。
神经网络调参的常用方法是,首先创建一个大到足以过拟合的网络,确保这个网络可以对任务进行学习。知道训练数据可以被学习之后,要么缩小网络,要么增大alpha来增强正则化,这可以提高泛化性能。
如何学习模型或用来学习参数的算法,这一点由solver参数设定。solver有两个好用的选项,默认的选型是‘adam’,在大多数情况下效果都很好,但对数据的缩放相当敏感(因此,始终将数据缩放为均值为0,方差为1是很重要的)。另一个选项是‘lbfgs’,其鲁棒性相当好,但在大型模型或大型数据集上的时间会比较长。还有更高级的‘sgd’选项,许多深度学习研究人员都会用到。‘sgd’选项还有许多其他参数需要调节,以便获得最佳结果。