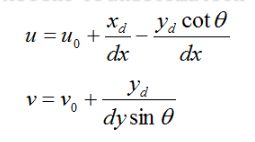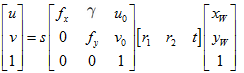【机器视觉】—— 相机成像过程坐标变化（世界坐标系、相机坐标系、图像坐标系、像素坐标系）

目录

一、四个坐标

二、两个坐标系的相互转换（齐次矩阵）

三、世界坐标系转（Ow）化为相机坐标系（Oc）

四、相机坐标系（Oc）与图像坐标系（Ox-y）

五、图像坐标系（Ox-y）与像素坐标系（Ou-v）

问题2(1)：图像坐标系mm怎么转换为piex，即怎么计算成像平面中的1piex = dxmm （即计算dx,dy）

问题2(2)：怎么计算u0,v0（图像坐标系原点相对于像素坐标系的位置）

六、世界坐标系到像素坐标系

 问题3：什么是相机的内外参？

相机内参（dx,dy,u0,v0,f）

相机外参（旋转矩阵R、平移矩阵T）

问题4：相机的内外参该怎么求解？

问题5：什么时候需要重新标定呢？

---

参考：https://blog.csdn.net/chentravelling/article/details/53558096

建议先阅读文章：原创 【机器视觉】——相机镜头篇  再阅读此篇文章

一、四个坐标

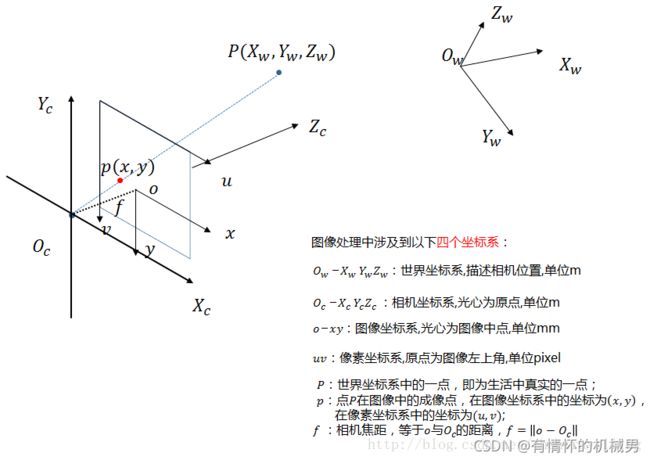
图像处理、立体视觉等等方向常常涉及到四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

 add：

世界坐标系：用于描述相机的位置，一般是一个固定的坐标系，对于机械臂视觉（相机固定型）来说，一般以机械臂基座为原点，用来分配各节机械臂的旋转与移动量（运动量）进而指导手臂抵达物体的位置；在双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。单位为m

相机坐标系：用于描述物体相对于相机的物理位置。以光心为原点，光心指的是凸透镜的中心，一般位于镜头上。单位为m

图像坐标系：用于描述物体在成像平面上的位置。图像坐标系的原点为相机光轴与成像平面的交点（即相机坐标系原点和图像坐标系原点都在光轴上，因此这两个原点的距离也是焦距f,单位mm），通常情况下是成像平面的中点（即图像中点）或者叫principal point。可以理解为物体成像后相对于在芯片上的位置。单位为mm。

像素坐标系：坐标原点为成像平面的左上角，单位为piex

问题：

1、四个坐标系的关系是什么，怎么转换？

2、像素坐标系的单位为piex，其他的坐标系单位为物理单位（m,mm）,怎么转换？

3、相机内参与外参是什么？

带着这些问题我们继续下面的学习——————————————————

二、两个坐标系的相互转换（齐次矩阵）

从一个坐标系到另一个坐标系，涉及到旋转和平移（其实所有的运动也可以用旋转矩阵和平移向量来描述）。绕着不同的坐标轴旋转不同的角度，得到相应的旋转矩阵，如下图所示：

基本步骤为：

1）先绕x,y,z轴旋转不同的角度，得到旋转矩阵，目的是旋转成和另一个坐标系的各个坐标轴平行且方向一致。

2）再进行平移，得到平移矩阵

3）完成

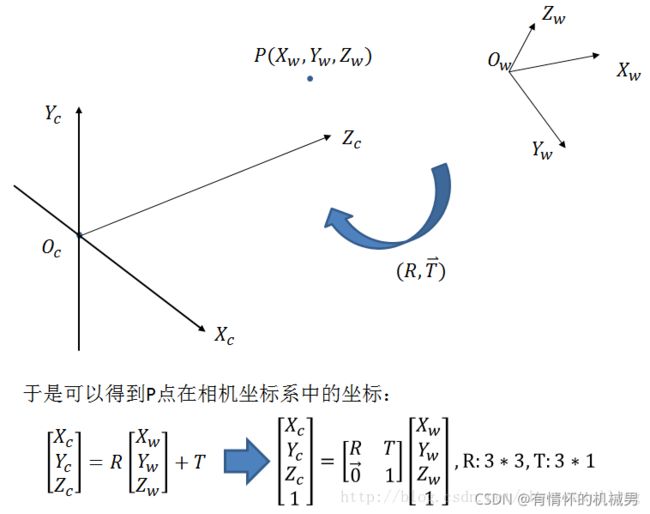
三、世界坐标系转（Ow）化为相机坐标系（Oc）

由二易得世界坐标系转化为相机坐标系的转化如下——刚性转换：

四、相机坐标系（Oc）与图像坐标系（Ox-y）

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

3D转到2D,这时候相机坐标系和图像坐标系的原点在一条线上起到了很大的作用，其实就是一个缩小操作，其中z方向的位置压缩在了成像平面上。其中f为焦距

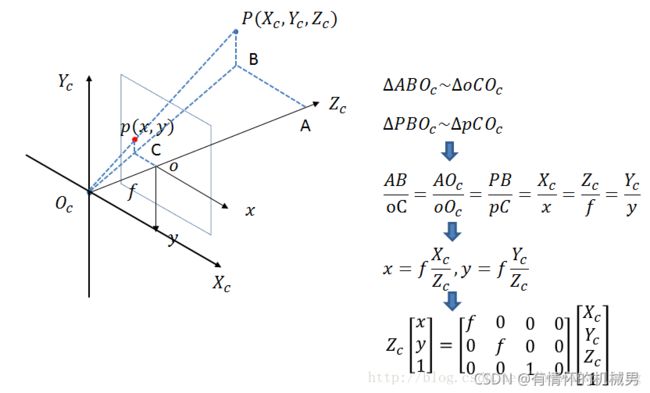
此时投影点p的单位还是mm，并不是pixel，需要进一步转换到像素坐标系。

ATTENTION：

从相机坐标系到图像坐标系，上面是理想的图像坐标系，但是实际过程中，往往会因为透镜制造误差和安装误差，造成畸变的现象，因此常常需要先对从相机坐标系转化为理想坐标系，然后将理想图像坐标系转化为实际图像坐标系，再进行实际图像坐标系转化为像素坐标系。这里先不考虑，具体可以看文章：https://blog.csdn.net/qq_45769063/article/details/120116186

五、图像坐标系（Ox-y）与像素坐标系（Ou-v）

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy代表每一个像素代表多少mm，即1pixel=dx mm

若UV垂直，则有：

若uv不垂直，则有：

参考：https://blog.csdn.net/a083614/article/details/78579163

 

 

问题2(1)：图像坐标系mm怎么转换为piex，即怎么计算成像平面中的1piex = dxmm （即计算dx,dy）

成像平面其实就是相机芯片，大小在物理上和芯片大小是一样的，一般相机买来是已知的，假设芯片大小为：h*w，单位mm，相机拍摄得到的图像大小为H*W，单位piex

则根据芯片大小和图像大小就可以求出dx,dy

芯片尺寸计算：参考https://blog.csdn.net/qq_45769063/article/details/120096212#t19

问题2(2)：怎么计算u0,v0（图像坐标系原点相对于像素坐标系的位置）

 u0,v0:表示，单位为piex,因为图像坐标系也是成像平面的中心，假设成像平面大小为h*w（其实就是芯片尺寸），则图像坐标系原点为在成像平面上的位置为（h//2,w//2）

芯片尺寸计算：参考https://blog.csdn.net/qq_45769063/article/details/120096212#t19

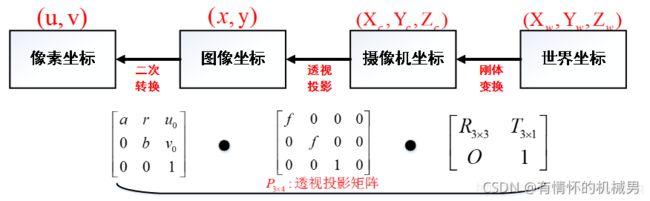
六、世界坐标系到像素坐标系

那么通过上面四个坐标系的转换就可以得到一个点从世界坐标系如何转换到像素坐标系的。

像素坐标系两坐标轴不垂直时：

 其中，u、v表示像素坐标系中的坐标，s表示尺度因子（1/zc)，fx、fy、u0、v0、γ（由于制造误差产生的两个坐标轴偏斜参数，通常很小）表示5个相机内参，R,t表示相机外参，Xw、Yw、Zw（假设标定棋盘位于世界坐标系中Zw=0的平面）表示世界坐标系中的坐标。

像素坐标系两坐标轴垂直时：

 问题3：什么是相机的内外参？

相机内参（dx,dy,u0,v0,f）

1）dx,dy:表示1piexl代表的mm数，单位为mm/piex，具体求解见问题2(1)，由问题2(1)可以知道求解dx和dy涉及到了芯片尺寸和分辨率

2）u0,v0:表示图像坐标系原点相对于像素坐标系的位置。由问题2（2）可以知道求解u0和v0涉及到dx,xy，即涉及到芯片尺寸和分辨率

3）f:相机焦距

因此相机内参主要指的是：芯片尺寸、分辨率、焦距

相机内参主要涉及的过程为：相机坐标系到像素坐标系的转换过程

因此相机焦距的改变会影响内参的改变

相机外参（旋转矩阵R、平移矩阵T）

旋转矩阵R，平移矩阵T主要涉及的过程是世界坐标系到相机坐标系的刚性转换过程

因此相机的位置发生变化会导致旋转矩阵R和平移矩阵T的变化

问题4：相机的内外参该怎么求解？

1）求解相机内外参的过程称之为标定

2）相机的内参和外参可以通过张正友标定获取。

3）通过最终的转换关系来看，一个三维中的坐标点，的确可以在图像中找到一个对应的像素点。

4）但是反过来，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的Zc的值。这涉及到三维重建知识，这里不展开。

问题5：什么时候需要重新标定呢？

1）更换相机（内外参均发生改变）

2）相机焦距发生改变（外参不变，内参改变）

3）相机位置发生改变（即相机坐标系发生了变化，引起了外参的变化，内参不变）