python--xarray介绍2
xarray介绍2
文章目录
- **xarray介绍2**
-
- **xarray.align**
- **xarray --降维处理**
- **xarray--分割数据**(以nc文件为例)
-
- xarray.DataArray.groupby()求季节平均、年平均、月平均
- 对于按月分组元素的迭代
- 分组元素的逐个访问
- 查找各个分组中对应元素在原始数据中键的位置
- xarray--分箱(按照不同区间对数据进行分组)
-
- 1、筛选数据groupby
- 2、应用数据Apply
- 3、具体绘图实操
- xarray--重采样
- xarray--时间窗移动
- xarray--线性多项式回归
xarray.align
给定任意数量的 Dataset 和/或 DataArray 对象,返回新的 具有对齐索引和尺寸大小的对象。
举个例子:
x = xr.DataArray( [[25, 35], [10, 24]],
dims=("lat", "lon"),
coords={"lat": [35.0, 40.0], "lon": [100.0, 120.0]},)
y = xr.DataArray( [[20, 5], [7, 13]],
dims=("lat", "lon"),
coords={"lat": [35.0, 42.0], "lon": [100.0, 120.0]},)
首先创建两个dataArray:
默认返回join='inner’的对齐方式,提取两者变量索引交集的数据。:
a, b = xr.align(x, y)
对比x、y可以发现,两者索引交集为lat=35,lon=100、120,
所以a就是x中lat=35,lon=100、120对应的值,b同理
同样的,可以改变join=‘Method ‘改变提取的结果。
方法outer:提取两者变量索引并集的数据。
a, b = xr.align(x, y, join="outer")
可以发现,将x、y的不同的lat对应的数据进行并集,a赋值结果如下
lon:100 120
- lat:35 25 35
- 40 10 24
- 42 nan nan
其他方法可以查看官网:
xarray.align
xarray --降维处理
举一个三维SST的例子进行处理示范:
import xarray as xr
file='..\\sst_olr\\olr.mon.mean.nc'
data=xr.open_dataset(file)
使用
data.shape
查看一些维度排列顺序
可以看到,维度顺序依次是time、lat、lon,对应axis=0、1、2
如果要对时间方向上以平均的方法进行降维,可写为:
# 对第0维度(维度time)以平均的方法进行降维
data.mean(axis = 0)
可用.plot方法可视化结果:
data.mean(axis=2).plot
同样的道理,如果要对经纬方向上进行降维,只需要将写上对应的维度即可。
# 对经纬度(维度lat、lon)以平均的方法进行降维
data.mean(axis=(1, 2))
这其实就得到了一个时间序列,这个时间序列描述了全球平均OLR的变化。
画个图来看看:
# 绘制2018-01~2018-12全球平均OLR变化
data.mean(axis=(1, 2)).sel(time=slice("2018-1","2018-12")).plot()
上述方法是仿照numpy中的降维方法,xarray中可以使用另一种更方便快捷的方法。直接选择需要处理的维度名称,效果与上述方法是一样的,建议大家采取xarray的方法,自动跳过了缺测值(默认),有利于数据处理。
data.mean(dim="time")data.mean(dim="lat","lon")
此外,如min(取最小值), max(取最大值), sum(求和), std(求标准差)等也可以实现降维,大家可以自己摸索。
xarray–分割数据(以nc文件为例)
在分割数据过程中,需要用到groupby()实现对于按季节、按月份的分割等待操作。
import xarray as xr
file='D:\\desktopppp\\20210906\\sst_olr\\olr.mon.mean.nc'
data=xr.open_dataset(file).olr
首先还是导入OLR数据,并提取时间变量,用法前文已经讲过
data.time
同时,这里的time是datatime的格式,可以直接使用datatime库的相关使用方法创建时间变量的待索引对象,利用.dt.month提取各个时间的月份数据
data.time.dt.month
同理,利用.dt.year提取各个时间的年份数据
data.time.dt.year
xarray.DataArray.groupby()求季节平均、年平均、月平均
类似于Pandas包中的groupby的思想,我们利用dataArray.groupby()函数将月份作为键(唯一值)来对原数据进行分离。本质是即把各年的某个月的数据放到了一组。
month_group = data.groupby("time.month")
month_group
除了可以以月份进行分割数据,也可以将年、季节作为分割对象,大家可以自行尝试
data.groupby("time.year")
data.groupby("time.season")
以上操作的优点在于,对于我们经常处理的一些海洋气象nc文件,经常需要对于数据进行求季节平均,月平均,年平均等处理,使dataArray.groupby()
就可以非常方便快捷的实现处理,以下给出例子:
season_mean=data.groupby('time.season').mean('time', skipna=True)
year_mean=data.groupby('time.year').mean('time', skipna=True)
month_mean=data.groupby('time.montn').mean('time', skipna=True)
对于按月分组元素的迭代
经过上面的分割操作后,原数据已经拆分成12个组(groups),放置在变量month_group中。对于这12个组,可通过循环进行遍历。迭代器返回各个组的键(组名)和值(与该组相对应的实际数据集)。
for group_name, group_ds in month_group:
# 当第一个循环结束时,停止遍历
month_group
print(group_name)
break
group_ds
分组元素的逐个访问
通过对数据进行list处理,可以获得分组名称和对应的xarray数据.
list_group = list(month_group)
list_group
这样,list_group中有12个DataArray,每个DataArray中对应包含1-12个月的数据
通过索引可以提取对于月份的数据
list_group[0]#访问这个分组对应的xarray数据(即各年的一月数据)。
list_group[1]#(即各年的二月数据)。以此类推
查找各个分组中对应元素在原始数据中键的位置
对于上述分割的数据,可以通过使用.groups方法获得元素(month)在原分组坐标中(time)的位置
gb = data.groupby("time.month").groupsgb
其中,第0个可理解为ds.isel(time = 0),同理第12个可理解为ds.isel(time = 12),并且是一个字典类型。字典:键值对(key-value pair)键与值之间的关联。
可以使用for循环遍历:
for key in sorted(gb): # str()函数将数值转为字符串
print( str(key)+"月", gb[key])
xarray–分箱(按照不同区间对数据进行分组)
1、筛选数据groupby
对数据进行筛选,按照自己定义的区间。
使用的数据信息如下:
为了减少运算时间,先选出第0时刻的数据,创建区间,按照区间进行筛选
da= data.isel(time = 0)
sst_bin = [-10, 0, 10, 20, 30]
gb_bin_list =da.groupby_bins("sst", sst_bin)
gb_bin_list
应该有四个区间,检验结果,符合要求
然后,对于所需区间的数据进行分别处理,索引方法与上述相同。
2、应用数据Apply
通过.groupby方法定义了原数组的分组方法,但是并未对原数组进行真正的分割。
下一步操作便是把相关的计算函数应用(Apply)到这12个分组了,使用的方法是.map(映射)
以求解多年各月sst平均空间场为例说明其实现过程:
import xarray as xr
import numpy as np
file='...\\sst.mnmean.nc'
data=xr.open_dataset(file)
gb = data.groupby("time.month")
def time_mean(a):
return a.mean(dim="time")
monthsst = gb.map(time_mean)
monthsst
monthsst = gb.mean(dim = "time")#直接实现计算
3、具体绘图实操
下面给出一些绘图操作:
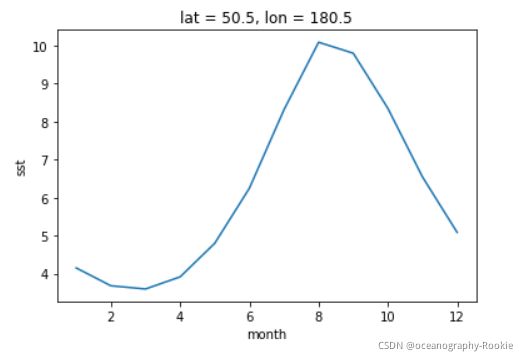
#绘制lon=180.5,lat=50.5处的数据时间序列
monthsst.sst.sel(lon=180.5, lat=50.5).plot()
#多年纬度月平均气候场
monthsst.sst.mean(dim="lon").plot.contourf(x="month", levels=12, vmin=-2, vmax=30)
具体参数设置如下:
- 绘制等值线图:
.plot.contourf; - x轴为变量
month:x="month"; - 色标分为12个部分(11个色块):
levels=12; - 绘制的最大值和最小值为30和-2:
vmin=-2, vmax=30.
#多年2月与7月平均气候场之间的差异
(monthsst.sst.sel(month=2) - monthsst.sst.sel(month=8)).plot()
xarray–重采样
import xarray as xr
import numpy as np
file='..\\sst.mnmean.nc'
data=xr.open_dataset(file)
ds = data.sel(time=slice("1989", "2018")).load()
resample_obj = ds.resample(time="5Y")
这里.resample(time="5Y")是对如何对时间进行重采样进行设置,维度为time,设置的时间间隔为 5 年。
需要注意的是:resample 仅能用于正确的日期、时间索引。
xarray–时间窗移动
可适用于任意维度,如果将其作用于时间维度,也可称之为滑动平均。
sst_rolling = ds.sst.rolling(time=12, center = True).mean()
参数time=12指定了对维度time以 12 个月为周期(月数据)变动时间窗,center参数表明以当前窗的两侧筛选数据,否则是以当前窗的前 12 个月作为筛选目标(包括本身)。.mean()表明对每一个 Rolling 对象取平均。
若时间窗为偶数值,那么对应中心位置将会在平均位置偏右侧,若不指定参数center=True,则采用从当前元素往上筛选的方法,否则采用以当前元素为中心,从两个方向上进行筛选。
xarray–线性多项式回归
import xarray as xr
import numpy as np
file='..\\sst.mnmean.nc'
data=xr.open_dataset(file)
ds = data.sel(time=slice("1989", "2018")).load()ds.sst.polyfit("time", 1, full = True)
#线性趋势(斜率)
ds.sst.polyfit("time", 1, full = True).polyfit_coefficients.isel(degree = 0).plot()
.polyfit方法实现了回归功能,第一个参数"time"指定拟合坐标为time,第二数字参数指定为一元线性回归,full = True代表回归方法不仅要返回拟合系数(一元回归即斜率和截距)还应当返回残差,矩阵秩和奇异值。
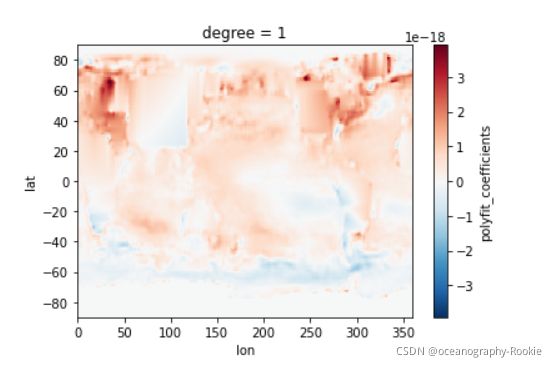
#截距空间分布
ds.sst.polyfit("time", 1, full = True).polyfit_coefficients.isel(degree = 1).plot()