利用人工智能预测乐高包装的LEGO商标尺寸，深入研究竟有惊人发现
导语：不知道大家会不会有天突发奇想，想知道乐高包装上的经典红底白字LOGO的尺寸，到底是标准统一的，还是设计师随缘用PS拖拽出来的？
笔者偶然看到一篇文字：大家有没有想过，乐高包装的LEGO商标尺寸是不是随缘的？
文章作者突然想到一个问题，如果乐高的LOGO尺寸是标准的，那能不能根据图片的比例关系计算出包装的尺寸？
从感官上可以理解，零件数越多的套装，包装就越大，那么就会采用越大的LOGO。但是很快这个美好的猜测就破灭了，通过数据可以看出，不少巨型套装，比如42115兰博基尼的logo，却是小的可怜
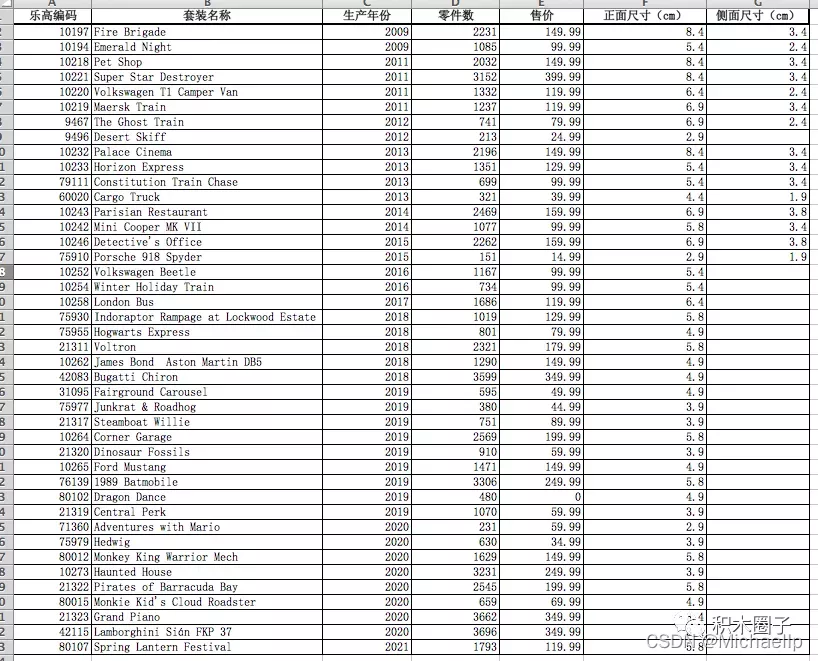
基于上述原因，这篇文章的作者就专门认真的去研究了40+个套装，然后把结果填写到Excel里面，继续分析。
----------------------------------------------------我是条分割线------------------------------------------------------------------------
当时作者迫于条件有限，只能用excel做简单的分析，这让我突发奇想， 能不能通过机器学习技术，利用多元线性回归来预测LEGO商标尺寸。
为此，我如数家珍地将我这几年的乐高盒子搬出来，以供研究。
逐一测量：
记录下编号和logo尺寸
一共57个套装，加上之前文章作者的42个数据， 一共99条实验数据（100条数据都不够T。T）
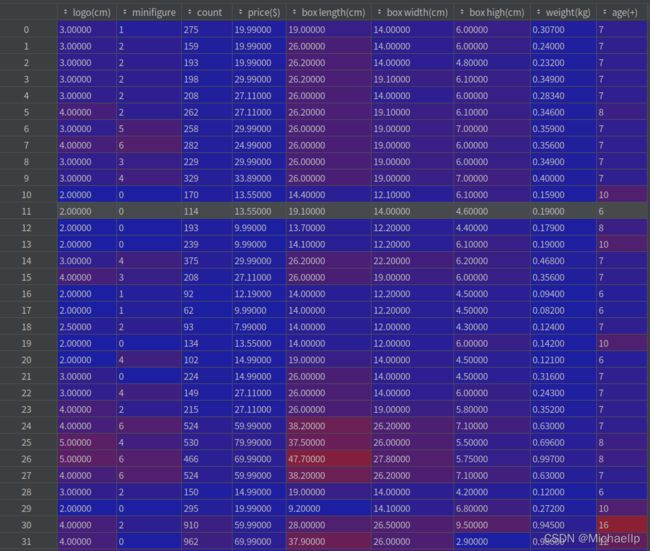
之前文章作者用到了生产年份， 零件数， 售价这三个维度。我觉得反正仍给机械读，何不扩展多几个维度。于是我添加了：
人仔个数， 实物长宽高，盒子的长宽高，重量，适合岁数。
这里感谢“积木圈子”这个公众账号，方便了我完善数据：
Python代码：
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
#通过read_csv来读取我们的目的数据集
lego_logo_data = pd.read_csv("lego-logo.csv")
#清洗不需要的数据
new_data = lego_logo_data.drop(labels=['name', 'number', 'year', 'date', 'real length(cm)', 'real width(cm)', 'real high(cm)'], axis=1)
#得到我们所需要的数据集且查看其前几列以及数据形状
print('head:', new_data.head(), '\nShape:', new_data.shape)
#热力图分析
a = pd.DataFrame(new_data)
fig,ax = plt.subplots(figsize=(16,16))
sns.heatmap(np.round(a.corr(),2),linewidths = 0.5,annot=True,ax=ax, vmax=1,vmin = 0, xticklabels=True , yticklabels=True, square=True)
ax.set_yticklabels(ax.get_xticklabels(), rotation=0,fontsize=16)
ax.set_xticklabels(ax.get_xticklabels(), rotation=90,fontsize=16)
plt.show()
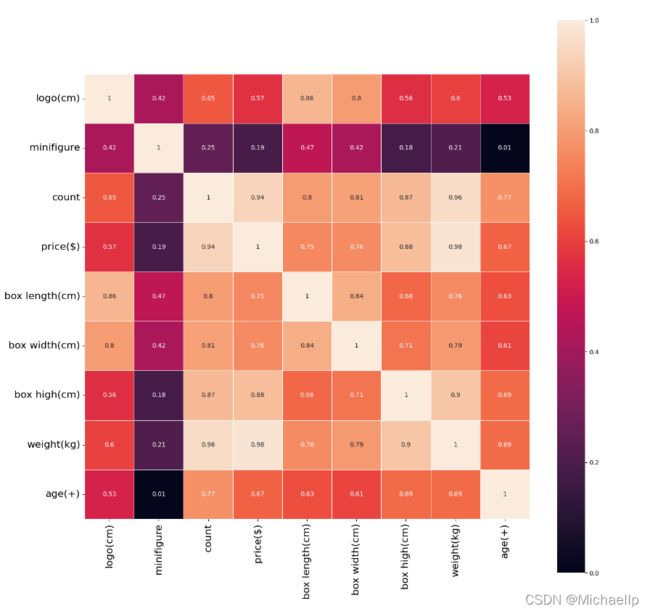
通过上面热力图可以看到， 和logo标签大小相关性最大的是盒子的长度，有0.85的相关性，其次就是盒子的宽度， 有0.8的相关性，最无相关性的是人仔数量， 只有0.42的相关性（都猜到人仔没什么相关性，没想到比年龄的相关性还要度，年龄也有0.53的相关性）。
接下来建立散点图来查看数据集里的数据分布。
seaborn的pairplot函数绘制X的每一维度和对应Y的散点图。通过设置size和aspect参数来调节显示的大小和比例。
通过加入一个参数kind=‘reg’，seaborn可以添加一条最佳拟合直线和95%的置信带。
sns.pairplot(new_data, x_vars=['minifigure', 'count', 'price($)', 'box length(cm)', 'box width(cm)', 'box high(cm)', 'weight(kg)', 'age(+)'], y_vars='logo(cm)', height=7, aspect=0.8, kind ='reg')
plt.savefig("pairplot.jpg")
plt.show()
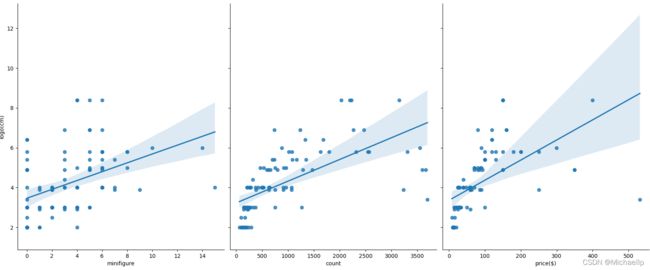
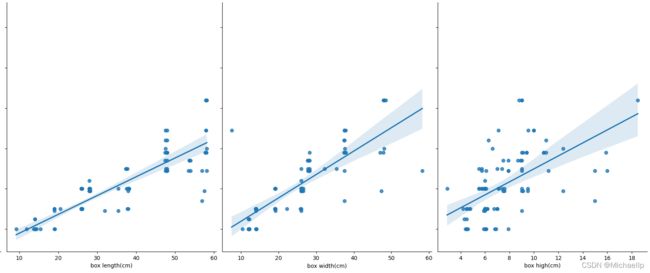
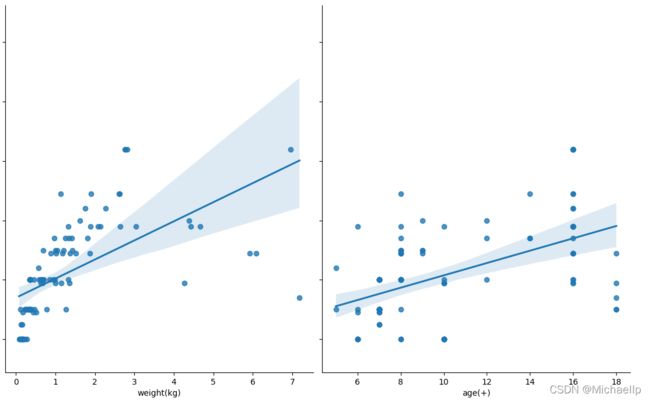物理可见，盒子长度(box length)的散点图分散的密度比较呈现出一条直线。
这里偷懒就没有，没有手写LinearRegression()，利用sklearn里面的包来对数据集进行划分，以此来创建训练集和测试集
train_size表示训练集所占总数据集的比例
X_train,X_test,Y_train,Y_test = train_test_split(new_data.iloc[:, 1:9], new_data['logo(cm)'], train_size=.80)
print("原始数据特征:", new_data.iloc[:, 1:9].shape,
",训练数据特征:", X_train.shape,
",测试数据特征:", X_test.shape)
print("原始数据标签:", new_data['logo(cm)'].shape,
",训练数据标签:", Y_train.shape,
",测试数据标签:", Y_test.shape)
model = LinearRegression()
model.fit(X_train,Y_train)
a = model.intercept_#截距
b = model.coef_#回归系数
print("最佳拟合线:截距",a,",回归系数：",b)
输出：
原始数据特征: (99, 8) ,训练数据特征: (79, 8) ,测试数据特征: (20, 8)
原始数据标签: (99,) ,训练数据标签: (79,) ,测试数据标签: (20,)
最佳拟合线:截距 0.041345452337445465 ,回归系数： [-2.05281380e-02 -2.78971278e-05 -1.23070046e-02 8.95558033e-02
4.13082677e-02 7.33723245e-02 3.84568201e-01 -3.09070948e-03]
R方检测
决定系数r平方
对于评估模型的精确度
y误差平方和 = Σ(y实际值 - y预测值)^2
y的总波动 = Σ(y实际值 - y平均值)^2
有多少百分比的y波动没有被回归拟合线所描述 = SSE/总波动
有多少百分比的y波动被回归线描述 = 1 - SSE/总波动 = 决定系数R平方
对于决定系数R平方来说
1） 回归线拟合程度：有多少百分比的y波动刻印有回归线来描述(x的波动变化)
2）值大小：R平方越高，回归模型越精确(取值范围0~1)，1无误差，0无法完成拟合
score = model.score(X_test,Y_test)
print(score)
输出
0.8009888167527538
对线性回归进行预测
Y_pred = model.predict(X_test)
print(Y_pred)
plt.plot(range(len(Y_pred)),Y_pred,'b',label="predict")
plt.figure()
plt.plot(range(len(Y_pred)),Y_pred,'b',label="predict")
plt.plot(range(len(Y_pred)),Y_test,'r',label="test")
plt.legend(loc="upper right") #显示图中的标签
plt.xlabel("the number of set")
plt.ylabel('value of logo(cm)')
plt.savefig("ROC.jpg")
plt.show()
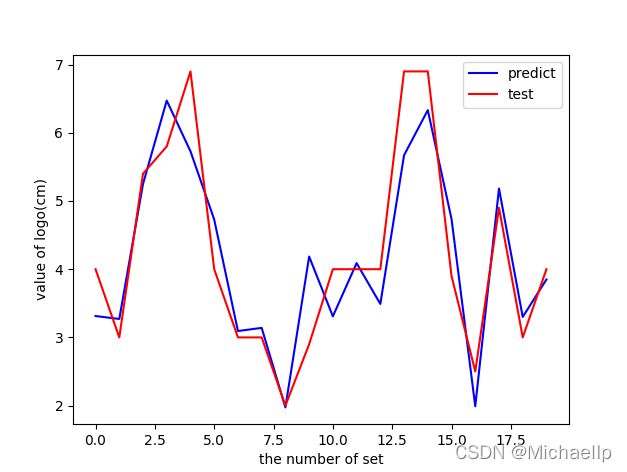红色是测试数据，蓝色是预测数据，R方去到0.8，看上去还行吧。
试下去掉人仔数和年龄，R方去到0.86，其实差不多。
0.8647729279218498
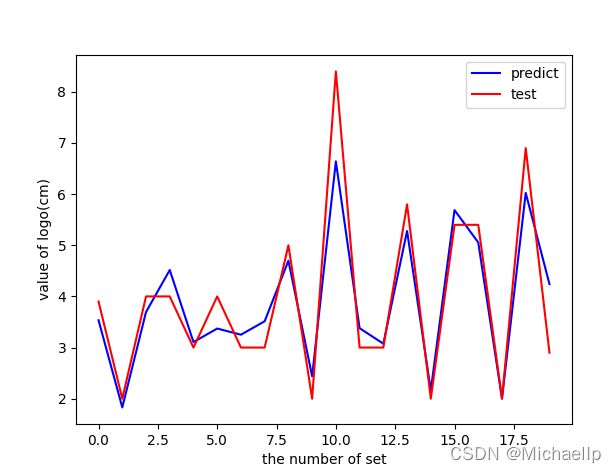
虽然还是没达到0.9，不过也表示相关性有点强了，能基本预测到logo大小。弥补了之前作者的局限。
后记 —— 预测价格
预测商标大小好像有点大材小用，既然有这么多个维度数据，不如预测下价格。
拿回之前的热力图，这里加入年份（year）
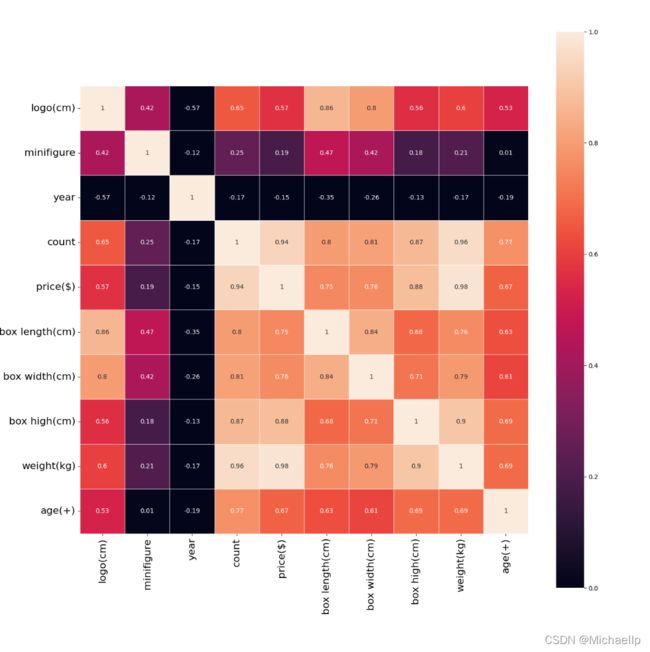
基于上面的热力图：
1.价格（price）那一行中, 本以为年份会和价格有关，没想到年份和价格还呈现弱的负相关（-0.15），也就是越来越便宜。。。我觉得这可能是数据量不够导致的，忽略它吧。
2.除此外，人仔数（minifigure）是最没有相关性的，只有0.19. 也就是人仔越多未必卖得越贵，而事实上人仔在玩家心目中还是很占分量的，人仔才是一个乐高套装的灵魂！
3.而相关性最大的是零件数量（count）和重量（weight），分别是0.94和0.98 。这个就很容易理解， 一分钱一分货，零件数越多，重量就越重， 价格也越贵。
某程度乐高还是有良心的，乐高完全可以抓住玩家心理，人仔越多卖越贵，而从数据上来说，乐高的定价都是base on零件成本。
然后我再去掉年份（year），标签大小（logo），人仔数（minifigure），年龄（age）。得出R2尽然竟然有。。。！
0.9866196081280411
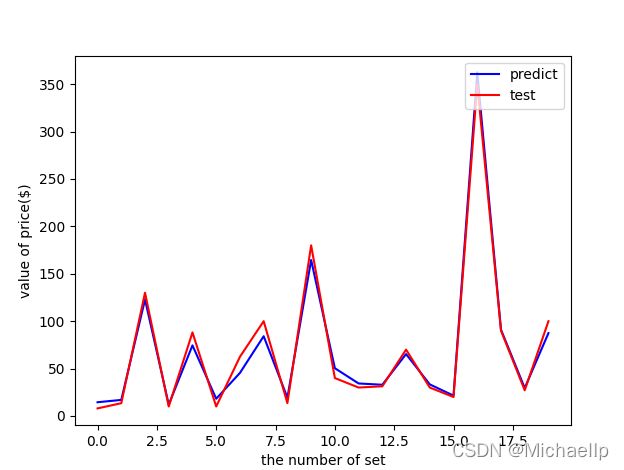0.98的R2值可以说很高了，也就是说，base on它零件数，盒子创宽高，重量，基本上可以预测到乐高套装的定价。
这也和坊间传闻“一个零件一块钱，多少零件多少钱“的概念大体一致啦。