暑假集训刷题记录
向上跳，再向上跳，也许再努力一点我就能够着菊苣们的膝盖了。
——题记
7.23
CodeForces 559C 组合数 + DP
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <map> 5 #define MP make_pair 6 #define F first 7 #define S second 8 using namespace std; 9 10 typedef long long LL; 11 typedef pair<LL, LL> Point; 12 13 const int maxn = 22000 + 10; 14 const LL MOD = 1000000007LL; 15 16 inline LL mul_mod(LL a, LL b) 17 { 18 a %= MOD; b %= MOD; 19 return (a * b) % MOD; 20 } 21 22 inline LL sub_mod(LL a, LL b) 23 { 24 return (((a - b) % MOD) + MOD) % MOD; 25 } 26 27 LL pow_mod(LL a, LL n) 28 { 29 LL ans = 1; 30 while(n) 31 { 32 if(n & 1) ans = mul_mod(ans, a); 33 a = mul_mod(a, a); 34 n >>= 1; 35 } 36 return ans; 37 } 38 39 LL Inverse(LL a) 40 { return pow_mod(a, MOD - 2); } 41 42 const int maxh = 200000 + 10; 43 44 LL fac[maxh], invfac[maxh]; 45 46 void init() 47 { 48 fac[0] = fac[1] = 1; 49 for(int i = 2; i < maxh; i++) fac[i] = mul_mod(fac[i-1], i); 50 invfac[maxh-1] = Inverse(fac[maxh-1]); 51 for(int i = maxh-2; i >= 0; i--) invfac[i] = mul_mod(invfac[i+1], i+1); 52 } 53 54 LL C(LL n, LL m) 55 { 56 if(m > n) { puts("shakalaka"); return 0; } 57 return mul_mod(mul_mod(fac[n], invfac[m]), invfac[n-m]); 58 } 59 60 int h, w, n; 61 62 Point a[maxn]; 63 64 LL methods(int i, int j) 65 { 66 LL x = a[j].first - a[i].first; 67 LL y = a[j].second - a[i].second; 68 return C(x + y, x); 69 } 70 71 LL dp[maxn]; 72 73 int main() 74 { 75 //freopen("in.txt", "r", stdin); 76 77 init(); 78 scanf("%d%d%d", &h, &w, &n); 79 for(int i = 1; i <= n; i++) 80 { 81 LL x, y; scanf("%I64d%I64d", &x, &y); 82 a[i] = MP(x, y); 83 } 84 sort(a + 1, a + n + 1); 85 a[0] = MP(1, 1); 86 a[n+1] = MP(h, w); 87 dp[1] = methods(0, 1); 88 89 for(int i = 2; i <= n + 1; i++) 90 { 91 dp[i] = methods(0, i); 92 for(int j = 1; j < i; j++) if(a[j].F <= a[i].F && a[j].S <= a[i].S) 93 dp[i] = sub_mod(dp[i], mul_mod(methods(j, i), dp[j])); 94 } 95 96 printf("%I64d\n", dp[n + 1]); 97 98 return 0; 99 }
CodeForces 219D 树形DP
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <vector> 5 using namespace std; 6 7 const int maxn = 200000 + 10; 8 int n; 9 10 vector<int> G[maxn]; 11 vector<bool> f[maxn]; 12 13 int L[maxn]; 14 int fa[maxn]; 15 int up[maxn]; 16 int rev[maxn]; 17 int totup; 18 19 void dfs(int u, int father, int d) 20 { 21 L[u] = d; 22 fa[u] = father; 23 for(int i = 0; i < G[u].size(); i++) 24 { 25 int v = G[u][i]; 26 if(v == father) continue; 27 if(!f[u][i]) { totup++; up[v] = up[u] + 1; } 28 else up[v] = up[u]; 29 dfs(v, u, d + 1); 30 } 31 } 32 33 int main() 34 { 35 //freopen("in.txt", "r", stdin); 36 scanf("%d", &n); 37 for(int i = 0; i < n-1; i++) 38 { 39 int u, v; scanf("%d%d", &u, &v); 40 G[u].push_back(v); f[u].push_back(true); 41 G[v].push_back(u); f[v].push_back(false); 42 } 43 44 dfs(1, 0, 0); 45 46 for(int v = 1; v <= n; v++) 47 rev[v] = totup - up[v] + L[v] - up[v]; 48 49 int ans = n - 1; 50 for(int i = 1; i <= n; i++) ans = min(ans, rev[i]); 51 52 printf("%d\n", ans); 53 54 vector<int> hehe; 55 for(int i = 1; i <= n; i++) if(rev[i] == ans) hehe.push_back(i); 56 57 printf("%d", hehe[0]); 58 for(int i = 1; i < hehe.size(); i++) printf(" %d", hehe[i]); 59 puts(""); 60 61 return 0; 62 }
7.24 补多校
7.25
CodeForces 445B Tire树上的博弈
1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 5 const int maxn = 100000 + 10; 6 const int sigma_size = 26; 7 8 int sz; 9 int ch[maxn][sigma_size]; 10 char str[maxn]; 11 12 void insert(char* s) 13 { 14 int u = 0; 15 for(int i = 0; s[i]; i++) 16 { 17 int c = s[i] - 'a'; 18 if(!ch[u][c]) ch[u][c] = sz++; 19 u = ch[u][c]; 20 } 21 } 22 23 bool win[maxn], lose[maxn]; 24 25 void dfs(int u) 26 { 27 bool isleaf = true; 28 for(int c = 0; c < 26; c++) if(ch[u][c]) 29 { 30 isleaf = false; 31 int v = ch[u][c]; 32 dfs(v); 33 win[u] |= !win[v]; 34 lose[u] |= !lose[v]; 35 } 36 if(isleaf) win[u] = false, lose[u] = true; 37 } 38 39 int main() 40 { 41 int n, k; scanf("%d%d", &n, &k); 42 43 sz = 1; 44 for(int i = 0; i < n; i++) 45 { 46 scanf("%s", str); 47 insert(str); 48 } 49 dfs(0); 50 51 if(!win[0]) puts("Second"); 52 else if(lose[0]) puts("First"); 53 else if(k & 1) puts("First"); 54 else puts("Second"); 55 56 return 0; 57 }
HDU 3996 网络流 最大权闭合图
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <vector> 5 #include <queue> 6 using namespace std; 7 8 typedef long long LL; 9 10 const int maxn = 3000; 11 const LL INF = 10000000000; 12 13 struct Edge 14 { 15 int from, to; 16 LL cap, flow; 17 Edge(int u, int v, LL c, LL f):from(u), to(v), cap(c), flow(f) {} 18 }; 19 20 struct Dinic 21 { 22 int n, m, s, t; 23 vector<Edge> edges; 24 vector<int> G[maxn]; 25 int d[maxn], cur[maxn]; 26 bool vis[maxn]; 27 28 void init() { for(int i = 0; i < n; i++) G[i].clear(); edges.clear(); } 29 30 void AddEdge(int u, int v, LL c) 31 { 32 edges.push_back(Edge(u, v, c, 0)); 33 edges.push_back(Edge(v, u, 0, 0)); 34 m = edges.size(); 35 G[u].push_back(m - 2); 36 G[v].push_back(m - 1); 37 } 38 39 bool BFS() 40 { 41 memset(vis, false, sizeof(vis)); 42 queue<int> Q; 43 Q.push(s); 44 vis[s] = true; 45 d[s] = 0; 46 47 while(!Q.empty()) 48 { 49 int u = Q.front(); Q.pop(); 50 for(int i = 0; i < G[u].size(); i++) 51 { 52 Edge& e = edges[G[u][i]]; 53 int v = e.to; 54 if(!vis[v] && e.cap > e.flow) 55 { 56 vis[v] = true; 57 d[v] = d[u] + 1; 58 Q.push(v); 59 } 60 } 61 } 62 63 return vis[t]; 64 } 65 66 LL DFS(int u, LL a) 67 { 68 if(u == t || a == 0) return a; 69 LL flow = 0, f; 70 for(int& i = cur[u]; i < G[u].size(); i++) 71 { 72 Edge& e = edges[G[u][i]]; 73 int v = e.to; 74 if(d[v] == d[u] + 1 && (f = DFS(v, min(a, e.cap-e.flow))) > 0) 75 { 76 flow += f; 77 e.flow += f; 78 a -= f; 79 edges[G[u][i]^1].flow -= f; 80 if(a == 0) break; 81 } 82 } 83 return flow; 84 } 85 86 LL MaxFlow() 87 { 88 LL flow = 0; 89 while(BFS()) 90 { 91 memset(cur, 0, sizeof(cur)); 92 flow += DFS(s, INF); 93 } 94 return flow; 95 } 96 }g; 97 98 int main() 99 { 100 int T; scanf("%d", &T); 101 for(int kase = 1; kase <= T; kase++) 102 { 103 int n; scanf("%d", &n); 104 g.n = n * 25 + 2; 105 g.init(); 106 g.s = 0; g.t = g.n - 1; 107 108 LL sum = 0; 109 for(int i = 0; i < n; i++) 110 { 111 int num; scanf("%d", &num); 112 for(int j = 1; j <= num; j++) 113 { 114 int x = i * 25 + j; 115 LL cost, value; 116 int rela; 117 scanf("%I64d%I64d%d", &cost, &value, &rela); 118 119 value -= cost; 120 if(value > 0) { g.AddEdge(0, x, value); sum += value; } 121 else g.AddEdge(x, g.t, -value); 122 123 while(rela--) 124 { 125 int a, b; scanf("%d%d", &a, &b); a--; 126 int y = a * 25 + b; 127 g.AddEdge(x, y, INF); 128 } 129 } 130 } 131 132 printf("Case #%d: %I64d\n", kase, sum - g.MaxFlow()); 133 } 134 135 return 0; 136 }
HDU 3472 网络流 混合图的欧拉路径
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 #include <queue> 7 using namespace std; 8 9 const int maxn = 30; 10 const int INF = 1000000000; 11 12 struct Edge 13 { 14 int from, to, cap, flow; 15 Edge(int u, int v, int c, int f):from(u), to(v), cap(c), flow(f) {} 16 }; 17 18 struct Dinic 19 { 20 int n, m, s, t; 21 vector<Edge> edges; 22 vector<int> G[maxn]; 23 int d[maxn], cur[maxn]; 24 bool vis[maxn]; 25 26 void init() { m = 0; for(int i = 0; i < n; i++) G[i].clear(); edges.clear(); } 27 28 void AddEdge(int u, int v, int c) 29 { 30 edges.push_back(Edge(u, v, c, 0)); 31 edges.push_back(Edge(v, u, 0, 0)); 32 m = edges.size(); 33 G[u].push_back(m - 2); 34 G[v].push_back(m - 1); 35 } 36 37 bool BFS() 38 { 39 memset(vis, false, sizeof(vis)); 40 queue<int> Q; 41 Q.push(s); 42 d[s] = 0; 43 vis[s] = true; 44 45 while(!Q.empty()) 46 { 47 int u = Q.front(); Q.pop(); 48 for(int i = 0; i < G[u].size(); i++) 49 { 50 Edge& e = edges[G[u][i]]; 51 int v = e.to; 52 if(!vis[v] && e.cap > e.flow) 53 { 54 vis[v] = true; 55 d[v] = d[u] + 1; 56 Q.push(v); 57 } 58 } 59 } 60 61 return vis[t]; 62 } 63 64 int DFS(int u, int a) 65 { 66 if(u == t || a == 0) return a; 67 int flow = 0, f; 68 for(int& i = cur[u]; i < G[u].size(); i++) 69 { 70 Edge& e = edges[G[u][i]]; 71 int v = e.to; 72 if(d[v] == d[u] + 1 && (f = DFS(v, min(a, e.cap-e.flow))) > 0) 73 { 74 flow += f; 75 e.flow += f; 76 a -= f; 77 edges[G[u][i]^1].flow -= f; 78 if(a == 0) break; 79 } 80 } 81 return flow; 82 } 83 84 int MaxFlow() 85 { 86 int flow = 0; 87 while(BFS()) 88 { 89 memset(cur, 0, sizeof(cur)); 90 flow += DFS(s, INF); 91 } 92 return flow; 93 } 94 }g; 95 96 const int maxm = 1000 + 10; 97 int n; 98 char word[30]; 99 100 int deg[maxn]; 101 102 bool occur[maxn]; 103 104 int pa[maxn]; 105 int findset(int x) { return x == pa[x] ? x : pa[x] = findset(pa[x]); } 106 void Union(int x, int y) 107 { 108 int px = findset(x), py = findset(y); 109 if(px != py) pa[px] = py; 110 } 111 112 int u[maxm], v[maxm], directed[maxm]; 113 int id[maxm]; 114 115 int main() 116 { 117 //freopen("in.txt", "r", stdin); 118 119 int T; scanf("%d", &T); 120 for(int kase = 1; kase <= T; kase++) 121 { 122 printf("Case %d: ", kase); 123 124 g.n = 28; 125 g.s = 26, g.t = 27; 126 g.init(); 127 int n; scanf("%d", &n); 128 129 for(int i = 0; i < 26; i++) pa[i] = i; 130 memset(id, 0, sizeof(id)); 131 memset(occur, false, sizeof(occur)); 132 memset(deg, 0, sizeof(deg)); 133 memset(directed, 0, sizeof(directed)); 134 for(int i = 0; i < n; i++) 135 { 136 scanf("%s%d", word, directed + i); 137 int l = strlen(word); 138 u[i] = word[0] - 'a'; 139 v[i] = word[l - 1] - 'a'; 140 occur[u[i]] = occur[v[i]] = true; 141 Union(u[i], v[i]); 142 deg[u[i]]++; deg[v[i]]--; 143 if(directed[i]) 144 { 145 id[i] = g.m; 146 g.AddEdge(u[i], v[i], 1); 147 } 148 } 149 150 //Judge the graph is connected 151 int root; 152 bool ok = true; 153 for(int i = 0; i < 26; i++) if(occur[i]) { root = findset(i); break; } 154 for(int i = 0; i < 26; i++) if(occur[i] && findset(i) != root) { ok = false; break; } 155 int cnt = 0; 156 for(int i = 0; i < 26; i++) if(deg[i] & 1) cnt++; 157 if((cnt != 0) && cnt != 2) ok = false; 158 if(!ok) { puts("Poor boy!"); continue; } 159 160 for(int i = 0; i < 26; i++) if(deg[i]) 161 { 162 if(deg[i] > 0) g.AddEdge(g.s, i, deg[i] / 2); 163 else if(deg[i] < 0) g.AddEdge(i, g.t, -deg[i] / 2); 164 } 165 g.MaxFlow(); 166 167 for(int i = 0; i < n; i++) if(directed[i]) 168 { 169 int x = id[i]; 170 if(g.edges[x].flow == 1) 171 { deg[u[i]] -= 2; deg[v[i]] += 2; } 172 } 173 174 int a1 = 0, a2 = 0; 175 for(int i = 0; i < 26; i++) if(deg[i]) 176 { 177 if(deg[i] == 1) a1++; 178 else if(deg[i] == -1) a2++; 179 } 180 if((a1 == 0 && a2 == 0) || (a1 == 1 || a2 == 1)) puts("Well done!"); 181 else puts("Poor boy!"); 182 } 183 184 return 0; 185 }
HDU 4183 网络流 每个点只能走一次的回路
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 #include <queue> 7 #include <cmath> 8 using namespace std; 9 10 const int maxn = 1000; 11 const int INF = 1000000000; 12 int n; 13 14 struct Edge 15 { 16 int from, to, cap, flow; 17 Edge(int u, int v, int c, int f):from(u), to(v), cap(c), flow(f) {} 18 }; 19 20 struct Dinic 21 { 22 int n, m, s, t; 23 vector<Edge> edges; 24 vector<int> G[maxn]; 25 int d[maxn], cur[maxn]; 26 bool vis[maxn]; 27 28 void init() { m = 0; edges.clear(); for(int i = 0; i < n; i++) G[i].clear(); } 29 30 void AddEdge(int u, int v, int c) 31 { 32 edges.push_back(Edge(u, v, c, 0)); 33 edges.push_back(Edge(v, u, 0, 0)); 34 m = edges.size(); 35 G[u].push_back(m - 2); 36 G[v].push_back(m - 1); 37 } 38 39 bool BFS() 40 { 41 memset(vis, false, sizeof(vis)); 42 queue<int> Q; 43 Q.push(s); 44 vis[s] = true; 45 d[s] = 0; 46 47 while(!Q.empty()) 48 { 49 int u = Q.front(); Q.pop(); 50 for(int i = 0; i < G[u].size(); i++) 51 { 52 Edge& e = edges[G[u][i]]; 53 int v = e.to; 54 if(!vis[v] && e.cap > e.flow) 55 { 56 vis[v] = true; 57 d[v] = d[u] + 1; 58 Q.push(v); 59 } 60 } 61 } 62 63 return vis[t]; 64 } 65 66 int DFS(int u, int a) 67 { 68 if(u == t || a == 0) return a; 69 int flow = 0, f; 70 for(int& i = cur[u]; i < G[u].size(); i++) 71 { 72 Edge& e = edges[G[u][i]]; 73 int v = e.to; 74 if(d[v] == d[u] + 1 && (f = DFS(v, min(a, e.cap-e.flow))) > 0) 75 { 76 flow += f; 77 e.flow += f; 78 a -= f; 79 edges[G[u][i]^1].flow -= f; 80 if(a == 0) break; 81 } 82 } 83 return flow; 84 } 85 86 int MaxFlow() 87 { 88 int flow = 0; 89 while(BFS()) 90 { 91 memset(cur, 0, sizeof(cur)); 92 flow += DFS(s, INF); 93 } 94 return flow; 95 } 96 }g; 97 98 const double eps = 1e-6; 99 100 int dcmp(double x) 101 { 102 if(fabs(x) < eps) return 0; 103 return x < 0 ? -1 : 1; 104 } 105 106 struct Pad 107 { 108 double freq, x, y, r; 109 bool operator < (const Pad& rhs) const 110 { return freq > rhs.freq; } 111 }a[maxn]; 112 113 bool Intersect(int i, int j) 114 { 115 double d = sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x) + (a[i].y-a[j].y)*(a[i].y-a[j].y)); 116 return dcmp(a[i].r + a[j].r - d) > 0; 117 } 118 119 int main() 120 { 121 //freopen("in.txt", "r", stdin); 122 123 int T; scanf("%d", &T); 124 while(T--) 125 { 126 scanf("%d", &n); 127 g.n = n * 2 - 1; 128 g.init(); 129 g.s = 0, g.t = n-1; 130 for(int i = 0; i < n; i++) 131 { 132 scanf("%lf%lf%lf%lf", &a[i].freq, &a[i].x, &a[i].y, &a[i].r); 133 } 134 sort(a, a + n); 135 136 if(Intersect(0, n-1)) { puts("Game is VALID"); continue; } 137 138 g.AddEdge(0, n, 2); 139 for(int i = 1; i < n - 1; i++) g.AddEdge(i, i + n, 1); 140 for(int i = 0; i < n; i++) 141 for(int j = i + 1; j < n; j++) 142 if(dcmp(a[i].freq - a[j].freq) > 0 && Intersect(i, j)) 143 g.AddEdge(i + n, j, INF); 144 145 if(g.MaxFlow() == 2) puts("Game is VALID"); 146 else puts("Game is NOT VALID"); 147 } 148 149 return 0; 150 }
CodeForces 461B 树形DP 跪舔题解
1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <vector> 5 using namespace std; 6 7 typedef long long LL; 8 9 const int maxn = 100000 + 100; 10 const LL MOD = 1000000000 + 7; 11 int n; 12 int color[maxn]; 13 vector<int> G[maxn]; 14 15 LL dp[maxn][2]; 16 17 void dfs(int u, int fa) 18 { 19 dp[u][color[u]] = 1; 20 for(int i = 0; i < G[u].size(); i++) 21 { 22 int v = G[u][i]; 23 if(v == fa) continue; 24 dfs(v, u); 25 dp[u][1] = ((dp[u][1] * (dp[v][0] + dp[v][1])) % MOD + (dp[u][0]*dp[v][1])%MOD)%MOD; 26 dp[u][0] = (dp[u][0] * ((dp[v][0] + dp[v][1])%MOD))%MOD; 27 } 28 } 29 30 int main() 31 { 32 scanf("%d", &n); 33 for(int u = 1; u < n; u++) 34 { 35 int v; scanf("%d", &v); 36 G[u].push_back(v); 37 G[v].push_back(u); 38 } 39 for(int i = 0; i < n; i++) scanf("%d", color + i); 40 dfs(0, -1); 41 printf("%I64d", dp[0][1]); 42 43 return 0; 44 }
7.26
CodeForces 455C 给出一个森林，可以合并两棵树。合并以后得到的新树的最小直径为
。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <vector> 5 using namespace std; 6 7 const int maxn = 300000 + 10; 8 int n, m, Q; 9 10 int diameter[maxn]; 11 12 bool vis[maxn]; 13 int pa[maxn]; 14 int findset(int x) { return x == pa[x] ? x : pa[x] = findset(pa[x]); } 15 void Union(int x, int y) 16 { 17 int px = findset(x), py = findset(y); 18 if(px != py) pa[px] = py; 19 } 20 21 vector<int> G[maxn]; 22 23 int len, id; 24 25 void dfs(int u, int fa, int d) 26 { 27 if(d > len) { len = d; id = u; } 28 for(int i = 0; i < G[u].size(); i++) 29 { 30 int v = G[u][i]; 31 if(v != fa) dfs(v, u, d + 1); 32 } 33 } 34 35 int longest(int v) 36 { 37 len = -1; 38 dfs(v, -1, 0); 39 len = -1; 40 dfs(id, -1, 0); 41 return len; 42 } 43 44 int main() 45 { 46 scanf("%d%d%d", &n, &m, &Q); 47 48 for(int i = 1; i <= n; i++) pa[i] = i; 49 while(m--) 50 { 51 int u, v; scanf("%d%d", &u, &v); 52 G[u].push_back(v); 53 G[v].push_back(u); 54 Union(u, v); 55 } 56 57 for(int i = 1; i <= n; i++) 58 { 59 int p = findset(i); 60 if(!vis[p]) 61 { 62 vis[p] = true; 63 diameter[p] = longest(p); 64 } 65 } 66 67 while(Q--) 68 { 69 int op, x, y; 70 scanf("%d%d", &op, &x); 71 if(op == 1) 72 { 73 printf("%d\n", diameter[findset(x)]); 74 } 75 else 76 { 77 scanf("%d", &y); 78 int px = findset(x), py = findset(y); 79 if(px == py) continue; 80 pa[px] = py; 81 int t = (diameter[px] + 1) / 2 + (diameter[py] + 1) / 2 + 1; 82 diameter[py] = max(diameter[px], max(diameter[py], t)); 83 } 84 } 85 86 return 0; 87 }
CodeForces 274B 树形DP
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <vector> 5 #include <algorithm> 6 using namespace std; 7 8 typedef long long LL; 9 10 const int maxn = 100000 + 10; 11 12 int n; 13 14 vector<int> G[maxn]; 15 LL val[maxn]; 16 LL add[maxn], sub[maxn]; 17 18 void dfs(int u, int fa) 19 { 20 for(int i = 0; i < G[u].size(); i++) 21 { 22 int v = G[u][i]; 23 if(v != fa) 24 { 25 dfs(v, u); 26 add[u] = max(add[u], add[v]); 27 sub[u] = max(sub[u], sub[v]); 28 } 29 } 30 val[u] += add[u] - sub[u]; 31 if(val[u] > 0) sub[u] += val[u]; 32 else if(val[u] < 0) add[u] += -val[u]; 33 } 34 35 int main() 36 { 37 scanf("%d", &n); 38 for(int i = 1; i < n; i++) 39 { 40 int u, v; scanf("%d%d", &u, &v); 41 G[u].push_back(v); 42 G[v].push_back(u); 43 } 44 for(int i = 1; i <= n; i++) scanf("%I64d", val + i); 45 46 dfs(1, -1); 47 printf("%I64d\n", add[1] + sub[1]); 48 49 return 0; 50 }
CodeForces 337D
题意：给出一棵n个节点的树，和m个特定的点。求这棵树中距所有这m个点的距离不超过d的点的个数。
题解本来是给的DP的做法，评论下面有个给出了一种更好的方法：用类似求树的直径办法求出这m个点中相距最远的两个点a、b，然后算出所有点到a、b的距离。最终答案所统计的点就是距a、b不超过d的点的个数。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 using namespace std; 7 8 const int maxn = 100000 + 10; 9 10 vector<int> G[maxn]; 11 12 int n, m, d; 13 14 int p[maxn]; 15 bool mark[maxn]; 16 17 int a, b; 18 19 int len, id; 20 21 void dfs1(int u, int fa, int d) 22 { 23 if(mark[u] && d > len) { len = d; id = u; } 24 for(int i = 0; i < G[u].size(); i++) 25 { 26 int v = G[u][i]; 27 if(v == fa) continue; 28 dfs1(v, u, d + 1); 29 } 30 } 31 32 int La[maxn], Lb[maxn]; 33 34 void dfs2(int u, int fa, int d, int* L) 35 { 36 L[u] = d; 37 for(int i = 0; i < G[u].size(); i++) 38 { 39 int v = G[u][i]; 40 if(v == fa) continue; 41 dfs2(v, u, d + 1, L); 42 } 43 } 44 45 int main() 46 { 47 //freopen("in.txt", "r", stdin); 48 49 scanf("%d%d%d", &n, &m, &d); 50 for(int i = 0; i < m; i++) 51 { 52 scanf("%d", p + i); 53 mark[p[i]] = true; 54 } 55 for(int i = 1; i < n; i++) 56 { 57 int u, v; scanf("%d%d", &u, &v); 58 G[u].push_back(v); G[v].push_back(u); 59 } 60 61 len = -1; 62 dfs1(p[0], 0, 0); 63 a = id; 64 len = -1; 65 dfs1(a, 0, 0); 66 b = id; 67 68 dfs2(a, 0, 0, La); 69 dfs2(b, 0, 0, Lb); 70 71 int ans = 0; 72 for(int i = 1; i <= n; i++) if(La[i] <= d && Lb[i] <= d) ans++; 73 printf("%d\n", ans); 74 75 return 0; 76 }
CodeForces 486D 树形DP 枚举集合中值最小的点(如果点一样的话就枚举取编号最小的那个)
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 using namespace std; 7 8 typedef long long LL; 9 10 const int maxn = 2000 + 10; 11 const LL MOD = 1000000007; 12 13 int d, n, root; 14 int a[maxn]; 15 vector<int> G[maxn]; 16 17 LL dfs(int u, int fa) 18 { 19 LL ans = 1; 20 for(int i = 0; i < G[u].size(); i++) 21 { 22 int v = G[u][i]; 23 if(v == fa) continue; 24 if(a[v] < a[root] || a[v] > a[root] + d) continue; 25 if(a[v] == a[root] && v < root) continue; 26 ans = (ans * (dfs(v, u) + 1)) % MOD; 27 } 28 return ans; 29 } 30 31 int main() 32 { 33 scanf("%d%d", &d, &n); 34 for(int i = 1; i <= n; i++) scanf("%d", a + i); 35 for(int i = 1; i < n; i++) 36 { 37 int u, v; scanf("%d%d", &u, &v); 38 G[u].push_back(v); G[v].push_back(u); 39 } 40 41 LL ans = 0; 42 for(int i = 1; i <= n; i++) 43 { 44 root = i; 45 ans = (ans + dfs(i, 0)) % MOD; 46 } 47 48 printf("%I64d\n", ans); 49 50 return 0; 51 }
POJ 3744 概率DP + 矩阵快速幂优化
先不考虑地雷，设f(x)表示走到位置x的概率。则有递推关系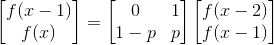
。所以在一段没有地雷的区间，可以快速计算走x步的概率。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 typedef double Mat[2][2]; 8 9 const int maxn = 12; 10 int n; 11 double p; 12 int pos[maxn]; 13 14 Mat A, E; 15 16 void mul(Mat A, Mat B, Mat ans) 17 { 18 Mat C; 19 memset(C, 0, sizeof(C)); 20 for(int i = 0; i < 2; i++) 21 for(int j = 0; j < 2; j++) 22 for(int k = 0; k < 2; k++) 23 C[i][j] += A[i][k] * B[k][j]; 24 memcpy(ans, C, sizeof(C)); 25 } 26 27 void pow(Mat A, int n, Mat ans) 28 { 29 Mat a, r; 30 memcpy(a, A, sizeof(a)); 31 memset(r, 0, sizeof(r)); 32 r[0][0] = r[1][1] = 1; 33 while(n) 34 { 35 if(n & 1) mul(r, a, r); 36 mul(a, a, a); 37 n >>= 1; 38 } 39 40 memcpy(ans, r, sizeof(r)); 41 } 42 43 int main() 44 { 45 //freopen("in.txt", "r", stdin); 46 47 while(scanf("%d", &n) == 1 && n) 48 { 49 scanf("%lf", &p); 50 for(int i = 0; i < n; i++) scanf("%d", pos + i); 51 sort(pos, pos + n); 52 n = unique(pos, pos + n) - pos; 53 54 if(pos[0] == 1) { puts("0.0000000"); continue; } 55 bool flag = false; 56 for(int i = 0; i + 1 < n; i++) if(pos[i] + 1 == pos[i+1]) { flag = true; break; } 57 if(flag) { puts("0.0000000"); continue; } 58 59 Mat x, t; 60 x[0][0] = 0; x[0][1] = 1; x[1][0] = 1- p; x[1][1] = p; 61 pow(x, pos[0] - 2, t); 62 double ans = t[1][1]; 63 64 for(int i = 1; i < n; i++) 65 { 66 ans *= 1.0 - p; 67 pow(x, pos[i]-pos[i-1]-2, t); 68 ans *= t[1][1]; 69 } 70 71 printf("%.7f\n", ans * (1.0 - p)); 72 } 73 74 return 0; 75 }