双指针算法理解+leetcode例题(Java实现)
双指针算法
- 双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。也可以延伸到多个数组的多个指针。
- 若两个指针指向同一数组,遍历方向相同且不会相交,则也称为滑动窗口(两个指针包围的区域即为当前的窗口),经常用于区间搜索。
- 若两个指针指向同一数组,但是遍历方向相反,则可以用来进行搜索,待搜索的数组往往是排好序的。
- 数组或字符串中,一般为左右指针,链表中一般为快慢指针。
例题
167. 两数之和 II - 输入有序数组
题解
- 因为数组已经排好序,我们可以采用方向相反的双指针来寻找这两个数字,一个初始指向最 小的元素,即数组最左边,向右遍历;一个初始指向最大的元素,即数组最右边,向左遍历。
- 如果两个指针指向元素的和等于给定值,那么它们就是我们要的结果。如果两个指针指向元 素的和小于给定值,我们把左边的指针右移一位,使得当前的和增加一点。如果两个指针指向元 素的和大于给定值,我们把右边的指针左移一位,使得当前的和减少一点。
public int[] twoSum(int[] numbers, int target) {
int[] answer = new int[2];
int sum;
//左指针
int start = 0;
//右指针
int end = numbers.length-1;
//终止条件 start==end 此时已经测试完所有可能的结果
while(start<end){
sum=numbers[start]+numbers[end];
if(sum==target){
answer[0]=start+1;
answer[1]=end+1;
break;
}
if(sum<target) start++;
//==和>=都会走该句 但前面==后break 故只有>=会走
else end--;
}
return answer;
}
88. 合并两个有序数组
题解
-
因为这两个数组已经排好序,我们可以把两个指针分别放在两个数组的末尾,即 nums1 的 m − 1 位和 nums2 的 n − 1 位。每次将较大的那个数字复制到 nums1 的后边,然后向前移动一位。 因为我们也要定位 nums1 的末尾,所以我们还需要第三个指针,以便复制。
public void merge(int[] nums1, int m, int[] nums2, int n) { //直接利用m和n指向两个数组已有元素的末尾 pos指向nums1末尾 int pos = m-- +n-- -1; while(m>=0&&n>=0){ //nums2的数较大时移向nums1末尾 if(nums1[m]<=nums2[n]){ nums1[pos--]=nums2[n]; n--; }else { nums1[pos--]=nums1[m]; m--; } } //如果 nums1的数字已经复制完,不要忘记把 nums2 的数字继续复制 while(n>=0){ nums1[n]=nums2[n]; n--; } }
633. 平方数之和
题解
- 这是一道经典的双指针相向而行的题目,但是要注意剪枝,就是right部分一定小于等于c的平方根,所以首先要把right部分确定下来,左右双向而行就可,大了就right左移,小了就left右移,直到相遇或者平方和为c,代码如下:
- 起始条件:左指针 0 右指针 c的平方根 (如果能与两个数的平方和相等,两个数一定在该范围内,在这个范围内进行双指针搜索),左右指针分别指示着较小和较大的数
- 终止条件:左指针大于右指针 或 c与两个数的平方和相等
public boolean judgeSquareSum(int c) {
int middle = (int) Math.sqrt(c);
int left = 0;//左指针
int right = middle;//右指针
long sum;//避免结果溢出
while(right>=left){
sum=left*left+right*right;
if(sum==c) return true;
if(sum>c) right--;
else left++;
}
return false;
}
680. 验证回文字符串 Ⅱ
题解
- 利用双指针不断更新判断是否为回文字符串
- 左指针和右指针对应的字符相同时,左指针右移,右指针左移,然后重新比较
- 两指针所对应的字符不等时,进行字符删除,并记录删除个数
- 终止条件 左指针大于右指针或要删除的字符个数>1
- 删除条件 两指针所对应的字符不等
- 重点就是判断删除左指针还是右指针的字符,要点是保证删除后字符串要为回文字符串。
public boolean validPalindrome(String s) {
//左指针 起始为字符串的开始位置
int left = 0;
int right = s.length() - 1;
char[] chars = s.toCharArray();
int deleteCount = 0;
char first;
char end;
//终止条件 左指针大于右指针
while (left <= right) {
//两指针所对应的字符不等 进行删除
if (chars[left] != chars[right]) {
if (deleteCount == 1) return false;
//删除左指针处字符符合回文的条件
if (chars[left + 1] == chars[right]) {
//验证左指针处字符删除后的下一个字符是否也相等 若相等则可以删除左指针处的字符 否则判断右指针处字符是否可以删除
//TODO 为什么只要下一组也符合就可以选了 因为字符串删错一个后下一个立即反映出来不再是回文字符串 若是字符串删除一个后为回文字符串 则删除错误的字符后 该字符串不再为回文字符串 只有删除正确才是回文
if (left + 2 < right) { //当左指针删除字符的下一个位置在 两个指针的包围区间内时 才要进行判断
if (chars[left + 2] == chars[right - 1]) {
left++;
deleteCount++;
continue;
}
} else {
left++;
deleteCount++;
continue;
}
}
//右指针左移符合的情况
if (chars[left] == chars[right - 1]) {
if (right - 2 >left) {
if (chars[left + 1] == chars[right - 2]) {
right--;
deleteCount++;
continue;
}
} else {
right--;
deleteCount++;
continue;
}
}
//无法通过删除一个得到回文字符串
return false;
}
//满足回文
left++;
right--;
}
return true;
}
- 另一解法:此解法在判断删除左指针还是右指针时,直接通过判断删完后范围内的字符串是否为回文字符串来判断删除哪个指针。
//如果s[i]==s[j]继续i++,j--,判断是否回文
//如果s[i]!=s[j]
//1.判断s[i+1]到s[j]范围内字符串是否回文,如果是,去掉s[i]即可
//2.或者判断s[i]到s[j-1]范围内是否回文,如果是,删除s[j]即可,
public boolean validPalindrome(String s) {
char[] ch=s.toCharArray();
for(int i=0,j=ch.length-1;i<j;i++,j--){
if(ch[i]!=ch[j]){
return isPalindrome(ch,i+1,j)||isPalindrome(ch,i,j-1);//不相等直接return 符合只可删一个的条件
}
}
return true;
}
//判断回文
public boolean isPalindrome(char[] s,int i,int j){
while(i<j){
if(s[i]!=s[j]){
return false;
}
i++;j--;
}
return true;
}
524. 通过删除字母匹配到字典里最长单词
题解:
-
因为题目说字典中最长字符串可以通过删除外字符串中的某些字符得到,
内字符串长度可以转化为外字符串所需删除字符的个数,因此我们只需比较外字符串还原为字典中符合条件的字符串需删除字符的数量即可,所删数量最小的符合内字符串即为所求。这里用数组统计个数。
-
利用双指针分别指示内字符和外字符串的尾部,逐个比较,不等时,外指针左移表示删除字符,并对对应内字符串删除字符个数加一,相等时,内外指针都左移。重复上述过程直到内外指针之一到尽头。
- 如果内字符串长度大于外字符串,该字符串不符合,记录数组对应位置置最大值。
- 这里还要判断内外字符串是否还有剩余
- 若内字符串还有剩余,则该内字符串不符合要求,将记录数组对应的值置为最大值
- 若外字符串还有剩余,此时让记录数组加上对应剩余个数即表示还原为对应内字符串应删除字符个数
-
之后,遍历记录数组,找到对应删除字符个数最少的索引即可。
public String findLongestWord(String s, List<String> dictionary) {
//遍历到内字符串的索引
int index = 0;
//内指针
int inRight;
//外指针
int outRight = s.length() - 1;
char[] temp;
//记录数组
int[] countDeleted = new int[dictionary.size()];
char[] chars = s.toCharArray();
//最小删除字符数
int least = Integer.MAX_VALUE;
//外字符串通过删除最少字符还原为内字符串的索引
int leastIndex = 0;
//对字典元素排序 按字典顺序拿结果
Collections.sort(dictionary);
//外循环终止条件
while (index < dictionary.size()) {
//获取当前内字符串
temp = dictionary.get(index).toCharArray();
//内指针
inRight = temp.length - 1;
//内字符串长度大于外字符串 直接跳过 该字符串不符合要求 不进行逐个字符的比较
if (inRight > outRight) {
outRight = s.length() - 1;
//置记录数组对应位置为最大值
countDeleted[index] = Integer.MAX_VALUE;
//去下个内字符串
index++;
continue;
}
//对内外字符串进行逐个字符的比较
//内循环终止条件
while (inRight >= 0 && outRight >= 0) {
if (chars[outRight] != temp[inRight]) {
//字符不等时 外指针左移
outRight--;
//记录数组对应数值加一
countDeleted[index]++;
} else {
//字符不等时 内外指针左移
outRight--;
inRight--;
}
}
//此时外字符串还有剩余
if (outRight >= 0) countDeleted[index] += outRight + 1;
//内部字符串还有剩余 该字符串不符合要求
if (inRight >= 0) countDeleted[index] = Integer.MAX_VALUE;
outRight = s.length() - 1;
//去下个内字符串
index++;
}
//外字符串删除最少的即为所求
for (int i = 0; i < countDeleted.length; i++) {
if (countDeleted[i] < least) {
least = countDeleted[i];
leastIndex = i;
}
}
//所有内字符串都不符合要求时
if (least == Integer.MAX_VALUE) return "";
return dictionary.get(leastIndex);
}
解法二:
-
我们也可以封装一个方法来判断内字符串是否为所符合的字符串
然后通过比较不断更新长度最长且字典顺序最小的字符串来获取最优解。
class Solution {
public String findLongestWord(String s, List<String> d) {
String result = "";
for (String t : d) {
if (isSubsequence(t, s)) {
// 获取长度最长且字典顺序最小的字符串
if (result.length() < t.length() || (result.length() == t.length() && result.compareTo(t) > 0)) {
result = t;
}
}
}
return result;
}
// 判断 t 是否为 s 的子序列
public boolean isSubsequence(String t, String s) {
int indext = 0, indexs = 0;
while (indext < t.length() && indexs < s.length()) {
if (t.charAt(indext) == s.charAt(indexs)) {
indext++;
}
indexs++;
}
return indext == t.length();
}
}
快慢指针
- 快慢指针就是定义两根指针,移动的速度一快一慢,以此来制造出自己想要的差值。
- 快慢指针常应用于链表中的查找相应的节点
常见应用
1.找中间值
- 一般的思路是:先遍历一次链表,记录住一共有多少个节点,然后,再次遍历找寻中点。
- 利用快慢指针,我们来看看这个问题会变成什么样。思路如下:我们把一个链表看成一个跑道,假设a的速度是b的两倍,那么当a跑完全程后,b刚好跑一半,以此来达到找到中间节点的目的。
2 判断链表中的环
- 还是把链表比作一条跑道,链表中有环,那么这条跑道就是一条圆环跑道,在一条圆环跑道中,两个人有速度差,那么迟早两个人会相遇,只要相遇那么就说明有环。
- 快慢指针中,因为每一次移动后,快指针都会比慢指针多走一个节点,所以他们之间在进入环状链表后,不论相隔多少个节点,慢指针总会被快指针赶上并且重合,此时就可以判断必定有环。
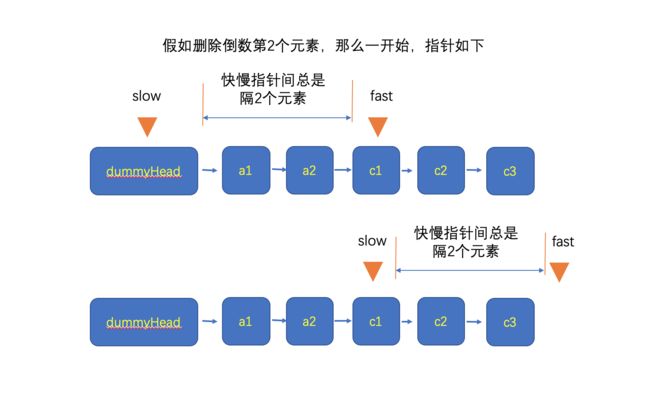
3 删除倒数第n个节点
- 删除倒数第n个节点,那就等于是要我们先找出待删除元素前一个元素,也就是倒数第n+1个节点。
- 那如何找倒数第(n+1)个元素呢?我们一开始就让fast指针比slow指针快n+1个元素,接下来,两个指针都是一步一步来往下走。那么当fast指针走完时,slow指针就刚刚好停留在倒数第(n+1)个元素上(slow比fast慢n+1)。
例题
142. 环形链表 II
题解
- 对于链表找环路的问题,有一个通用的解法——快慢指针(Floyd 判圈法)。给定两个指针, 分别命名为 slow 和 fast,起始位置在链表的开头。每次 fast 前进两步,slow 前进一步。如果 fast 可以走到尽头,那么说明没有环路;如果 fast 可以无限走下去,那么说明一定有环路,且一定存 在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时,我们将 fast 重新移动到链表开头,并 让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时,相遇的节点即为环路的开始点。
原理
设第一次环内相遇时,slow慢指针走了s部,fast快指针走了f部
链表中链表头部到环入口结点(不计环入口节点)有a个节点,环有b个节点
- f=2s (快指针每次2步,路程刚好2倍)
- f=s+nb (第一次相遇时,刚好多走了n圈)
推出 s=nb
从head结点走到入环点需要走 : a + nb, 而slow已经走了nb,那么slow再走a步就是入环点了。
如何知道slow刚好走了a步? 从head开始,和slow指针一起走,相遇时刚好就是a步。
//快慢指针解决
public ListNode detectCycle(ListNode head) {
//慢指针
ListNode slow = head;
//快指针
ListNode fast = head;
do{
//链表中无环的条件
if(fast==null||fast.next==null) return null;
//第一次相遇前快指针走两步,慢指针走一步
fast=fast.next.next;
slow=slow.next;
}while(fast!=slow);
//第一次相遇后 快指针置首部 并改为走一步
fast=head;
//环的起始位置为快慢指针第二次相遇的位置
while(fast!=slow){
fast=fast.next;
slow=slow.next;
}
return fast;
}
对撞指针
对撞指针是双指针算法之一。
对撞指针从两端向中间迭代数组。一个指针从始端开始,另一个从末端开始。
对撞指针的终止条件是两个指针相遇。
1 循环不变量
我们假设数组长度为len:
[0, left)中不含值为val的元素;(right, len - 1]中均为值为val的元素;
2设置变量初始值及循环终止条件
left = 0,保证[0,left)初始为空区间;
right = len - 1,保证(right, len - 1]初始为空区间;
当left > right时,上述两个区间完整覆盖数组所有元素,且得到left为去除后数组长度。
3例题
27. 移除元素
public int removeElement(int[] nums, int val) {
//尾指针
int index=nums.length-1;
int temp;
for(int i =0;i<nums.length;i++){
//循环终止条件
if(i>index) break;
//进行交换
if(nums[i]==val){
temp=nums[index];
nums[index]=nums[i];
nums[i]=temp;
index--;
i--;
}
}
//返回个数
return index+1;
}
滑动窗口
- 滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。
- 该技术可以将一部分问题中的嵌套循环转变为一个单循环,因此它可以减少时间复杂度。
- 简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。
- 可以用来解决一些查找满足一定条件的连续区间的性质(长度等)的问题。由于区间连续,因此当区间发生变化时,可**以通过旧有的计算结果对搜索空间进行剪枝,这样便减少了重复计算,降低了时间复杂度。**往往类似于“ 请找到满足 xx 的最 x 的区间(子串、子数组)的 xx ”这类问题都可以使用该方法进行解决。
- 滑动:说明这个窗口是移动的,也就是移动是按照一定方向来的。
- **窗口:**窗口大小并不是固定的,可以不断扩容直到满足一定的条件;也可以不断缩小,直到找到一个满足条件的最小窗口;当然也可以是固定大小。
76. 最小覆盖子串
题解:
利用滑动窗口思想,通过扩展和收缩滑动窗口,可以想象成一个窗口在字符串上游走,当这个窗口包含的元素满足条件,即包含字符串T的所有元素,记录下这个滑动窗口的长度,这些长度中的最小值就是要求的结果。
- 我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
- 我们先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
- 此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
- 重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,**第 2 步相当于在寻找一个「可行解」并记录这个滑动窗口的长度,然后第 3 步在优化这个「可行解」,最终找到局部最优解并记录这个滑动窗口的长度。**左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。最终找到最优解的滑动窗口的长度。
如何判断滑动窗口包含了T的所有元素?
-
使用数组记录窗口中所需各字符的数量。
-
一开始滑动窗口为空,用T中各元素来初始化这个
need,表示只需要t中对应的字符 -
当滑动窗口扩展或者收缩的时候,去维护这个need字典,例如当滑动窗口包含某个元素,我们就让need中这个元素的数量减1,代表所需元素减少了1个;当滑动窗口移除某个元素,就让need中这个元素的数量加1。
-
如果每次判断滑动窗口是否包含了T的所有元素?结论就是当
need中所有元素的数量都小于等于0时,表示当前滑动窗口不再需要任何元素。- 利用变量count来记录所需元素的总数量,当我们碰到一个所需元素
c,不仅need[c]的数量减少1,同时count也要减少1,这样我们通过count就可以知道是否满足条件,而无需遍历字典了。 - 前面也提到过,
need记录了遍历到的所有元素,而只有need[c]>0大于0时,代表c就是所需元素
- 利用变量count来记录所需元素的总数量,当我们碰到一个所需元素
public String minWindow(String s, String t) {
int[] need = new int[128];
//记录字符串t中每个字符的数量
for (char ch : t.toCharArray())
need[ch]++;
//字符串t的数量
int count = t.length();
int left = 0;//窗口的左边界
int right = 0;//窗口的右边界
//覆盖t的最小长度
int windowLength = Integer.MAX_VALUE;
//覆盖字符串t开始的位置
int strStart = 0;
while (right < s.length()) {
if (need[s.charAt(right++)]-- > 0)
count--;
//如果全部覆盖
while (count == 0) {
//如果有更小的窗口就记录更小的窗口
if (right - left < windowLength) {
windowLength = right - left;
strStart = left;
}
if (need[s.charAt(left++)]++ == 0)
count++;
}
}
//如果找到合适的窗口就截取,否则就返回空
if (windowLength != Integer.MAX_VALUE)
return s.substring(strStart, strStart + windowLength);
return "";
}