基于麻雀搜索算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、发现者位置更新
- 2、跟随者位置更新
- 3、警戒者位置更新
- 4、SSA算法伪代码
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
麻雀搜索算法(Sparrow Search Algorithm, SSA)是2020年提出的一种新兴的元启发式算法，它与粒子群算法、蜻蜓优化算法等同属于基于群体的社会化特征优化的群智能算法。该算法通过不断更新个体位置，模拟麻雀觅食和反捕食行为。相比传统算法，麻雀搜索算法的结构简单、易于实现，且控制参数较少，局部搜索能力较强。该算法在单峰、多峰等基准函数上的表现优于粒子群算法、蚁群算法等传统算法。
在麻雀搜索算法中，将个体区分为发现者、跟随者和警戒者，每个个体位置对应一个解。根据算法设定，警戒者所占种群比例10%~20%，而发现者和跟随者是动态变化的， 即一只个体成为发现者必然意味着另一只个体将成为跟随者。按照分工划分，发现者主要为整个种群提供觅食方向和区域，跟随者则是跟随发现者进行觅食，警戒者负责对于觅食区域的监视。在觅食过程中，通过不断更新三者位置，完成资源的获取。
设种群中有 n n n只麻雀，则由所有个体组成的种群可表示为 X = [ x 1 , x 2 , ⋯ , x n ] T X=[x_1,x_2,\cdots,x_n]^T X=[x1,x2,⋯,xn]T，个体各自对应的适应度函数为 F = [ f ( x 1 ) , f ( x 2 ) , ⋯ , f ( x n ) ] T F=[f(x_1),f(x_2),\cdots,f(x_n)]^T F=[f(x1),f(x2),⋯,f(xn)]T。具体表示为： X = [ x 1 , 1 x 1 , 2 ⋯ ⋯ x 1 , d x 2 , 1 x 2 , 2 ⋯ ⋯ x 2 , d ⋮ ⋮ ⋮ ⋮ ⋮ x n , 1 x n , 2 ⋯ ⋯ x n , d ] (1) X=\begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & \cdots & x_{1,d} \\x_{2,1} & x_{2,2} & \cdots & \cdots & x_{2,d} \\\vdots & \vdots & \vdots & \vdots & \vdots\\ x_{n,1} & x_{n,2} & \cdots & \cdots & x_{n,d} \\ \end{bmatrix}\tag{1} X=⎣⎢⎢⎢⎡x1,1x2,1⋮xn,1x1,2x2,2⋮xn,2⋯⋯⋮⋯⋯⋯⋮⋯x1,dx2,d⋮xn,d⎦⎥⎥⎥⎤(1) F = [ f ( [ x 1 , 1 x 1 , 2 ⋯ ⋯ x 1 , d ] ) f ( [ x 2 , 1 x 2 , 2 ⋯ ⋯ x 2 , d ] ) ⋮ f ( [ x n , 1 x n , 2 ⋯ ⋯ x n , d ] ) ] (2) F=\begin{bmatrix} f(\begin{bmatrix}x_{1,1} & x_{1,2} & \cdots & \cdots & x_{1,d}\end{bmatrix}) \\f(\begin{bmatrix}x_{2,1} & x_{2,2} & \cdots & \cdots & x_{2,d}\end{bmatrix})\\ \vdots\\ f(\begin{bmatrix}x_{n,1} & x_{n,2} & \cdots & \cdots & x_{n,d}\end{bmatrix}) \end{bmatrix}\tag{2} F=⎣⎢⎢⎢⎡f([x1,1x1,2⋯⋯x1,d])f([x2,1x2,2⋯⋯x2,d])⋮f([xn,1xn,2⋯⋯xn,d])⎦⎥⎥⎥⎤(2)
1、发现者位置更新
发现者的位置更新方式如下： x i , j t + 1 = { x i , j t ⋅ exp ( − i α × i t e r m a x ) , R 2 < S T x i , j t + Q ⋅ L , R 2 ≥ S T (3) x_{i,j}^{t+1}=\begin{dcases}x_{i,j}^t\cdot \exp(\frac{-i}{\alpha×iter_{max}}),R_2
2、跟随者位置更新
跟随者的位置更新方式如下： x i , j t + 1 = { Q ⋅ exp ( x w o r s t t − x i , j t i 2 ) , i > n 2 x P t + 1 + ∣ x i , j t − x P t + 1 ∣ ⋅ A + ⋅ L , i ≤ n 2 (4) x_{i,j}^{t+1}=\begin{dcases}Q\cdot\exp(\frac{x_{worst}^t-x_{i,j}^t}{i^2}),\quad\quad\quad\,\, i>\frac n2\\x_P^{t+1}+|x_{i,j}^t-x_P^{t+1}|\cdot \boldsymbol A^+\cdot L,\quad i≤\frac n2\end{dcases}\tag{4} xi,jt+1=⎩⎪⎨⎪⎧Q⋅exp(i2xworstt−xi,jt),i>2nxPt+1+∣xi,jt−xPt+1∣⋅A+⋅L,i≤2n(4)其中， x w o r s t t x_{worst}^t xworstt表示第 t t t代适应度最差的个体位置， x P t + 1 x_P^{t+1} xPt+1表示第 t + 1 t+1 t+1代中适应度最佳的个体位置。 A \boldsymbol A A表示 1 × dim 1×\dim 1×dim的矩阵，矩阵中每个元素随机预设为-1或1， A + = A T ( A A T ) − 1 \boldsymbol A^+=\boldsymbol{A^T}\boldsymbol{(AA^T)^{-1}} A+=AT(AAT)−1。跟随者位置更新方式可总结为：当 i > n 2 i>\frac n2 i>2n时，表示第 i i i个加入者的适应度较低，没有同发现者竞争食物的资格，需要飞往其他区域觅食；当 i ≤ n 2 i≤\frac{n}2 i≤2n时，加入者将在最优个体 x P x_P xP近觅食。
3、警戒者位置更新
警戒者位置更新方式如下： x i , j t + 1 = { x b e s t t + β ⋅ ∣ x i , j t − x b e s t t ∣ , f i ≠ f g x b e s t t + k ⋅ ( x i , j t − x b e s t t ∣ f i − f w ∣ + ε ) , f i = f g (5) x_{i,j}^{t+1}=\begin{dcases}x_{best}^t+\beta\cdot|x_{i,j}^t-x_{best}^t|,\quad\quad\,\, f_i≠f_g\\x_{best}^t+k\cdot(\frac{x_{i,j}^t-x_{best}^t}{|f_i-f_w|+\varepsilon}),\quad f_i=f_g\end{dcases}\tag{5} xi,jt+1=⎩⎨⎧xbestt+β⋅∣xi,jt−xbestt∣,fi=fgxbestt+k⋅(∣fi−fw∣+εxi,jt−xbestt),fi=fg(5)其中， x b e s t t x_{best}^t xbestt表示第 t t t代中全局最优位置， β \beta β为控制步长，服从均值为0，方差为1的正态分布， k ∈ [ − 1 , 1 ] k∈[-1,1] k∈[−1,1]， ε \varepsilon ε设置为常数，用以避免分母为0。 f i f_i fi表示当前个体的适应度值， f g f_g fg和 f w f_w fw表示目前全局最优和最差个体的适应度值。警戒者位置更新方式可总结为：当 f i ≠ f g f_i≠f_g fi=fg时，意味着该个体处于种群外围，需要采取反捕食行为，不断变换位置获得更高 的适应度；当 f i = f g f_i=f_g fi=fg时，意味着该个体处于种群中心，它将不断接近附近的同伴，以此远离危险区域。
4、SSA算法伪代码
二、仿真实验与分析
为了使算法更具说服力，在所有情况下，我们对每个测试函数进行30次独立试验。在每个实验中，迭代的最大次数为1000，种群大小设置为100( n = 100 n=100 n=100)。GWO的参数设置如下： a a a的值从2线性减少到0， r 1 , r 2 r_1,r_2 r1,r2是 [ 0 , 1 ] [0,1] [0,1]中的随机向量；PSO的参数为 c 1 = c 2 = 1.49445 , w = 0.729 c_1=c_2=1.49445,w=0.729 c1=c2=1.49445,w=0.729；GSA的参数为 G 0 = 100 , α = 20 G_0=100,\alpha=20 G0=100,α=20。SSA的参数设置如下：发现者数量和 S D SD SD分别占20%和10%， S T = 0.8 ST=0.8 ST=0.8。以文献[1]的F1、F2、F3为例。
下图为对比曲线。
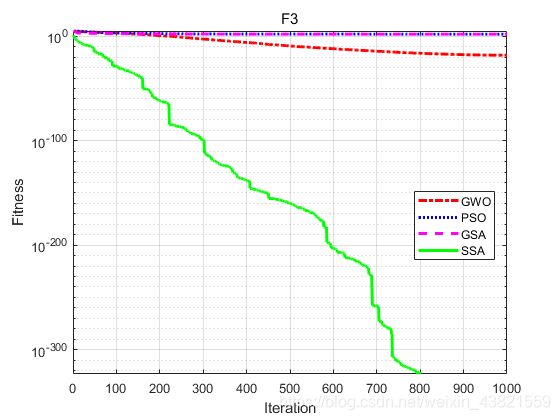最大值、最小值、平均值及标准差显示如下：
函数：F1
GWO：最大值: 1.9014e-90,最小值:1.1467e-93,平均值:2.6184e-91,标准差:5.3549e-91
PSO：最大值: 25.6849,最小值:2.8582,平均值:9.0364,标准差:5.9129
GSA：最大值: 6.5868e-18,最小值:2.3286e-18,平均值:4.0924e-18,标准差:1.0661e-18
SSA：最大值: 0,最小值:0,平均值:0,标准差:0
函数：F2
GWO：最大值: 8.0552e-52,最小值:4.8965e-54,平均值:1.5053e-52,标准差:2.105e-52
PSO：最大值: 14.9366,最小值:4.5229,平均值:8.2907,标准差:2.6433
GSA：最大值: 1.2197e-08,最小值:8.179e-09,平均值:1.0214e-08,标准差:9.821e-10
SSA：最大值: 9.1086e-306,最小值:0,平均值:3.0362e-307,标准差:0
函数：F3
GWO：最大值: 1.7551e-17,最小值:1.049e-25,平均值:7.2717e-19,标准差:3.1948e-18
PSO：最大值: 255.9549,最小值:38.1862,平均值:112.098,标准差:53.1931
GSA：最大值: 215.1596,最小值:44.459,平均值:106.1498,标准差:36.8177
SSA：最大值: 0,最小值:0,平均值:0,标准差:0
结果表明，该算法在搜索精度、收敛速度和稳定性等方面均优于现有算法。
三、参考文献
[1] Jiankai Xue, Bo Shen. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[2] 段玉先, 刘昌云. 基于Sobol序列和纵横交叉策略的麻雀搜索算法[J/OL].计算机应用:1-9 [2021-05-28].