基于蜉蝣优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、蜉蝣优化算法
-
- (1)雄性蜉蝣的更新
- (2)雌性蜉蝣的更新
- (3)蜉蝣的交配过程
- 2、MA算法伪代码
- 二、仿真实验与结果分析
-
- 1、函数测试与数值分析
- 2、WSN三维覆盖优化
- 三、参考文献
一、理论基础
1、蜉蝣优化算法
蜉蝣优化算法(Mayfly optimization algorithm, MA)是2020年由希腊学者Konstantinos等人提出的新的仿真优化算法,用于解决复杂的函数优化问题。
MA是由雌性蜉蝣群体和雄性蜉蝣群体组成,受蜉蝣的交配行为启发。交配行为中,雄性蜉蝣的最优个体和雌性蜉蝣的最优个体进行交配,得到一个最优子代;同理,雄性蜉蝣次优个体和雌性蜉蝣次优个体进行交配得到次优的子代,依此类推。这一过程符合优胜劣汰规律,逐步淘汰适应度较差的个体。
设雄性和雌性蜉蝣在 d d d维空间中的位置为 x = ( x 1 , x 2 , ⋯ , x d ) x=(x_1,x_2,\cdots,x_d) x=(x1,x2,⋯,xd),再根据预先设定的优化函数 f ( x ) f(x) f(x)进行搜索性能的评价。设蜉蝣个体在维度空间上的速度为 v = ( v 1 , v 2 , ⋯ , v d ) v=(v_1,v_2,\cdots,v_d) v=(v1,v2,⋯,vd),每个蜉蝣的飞行方向是个体和群体的飞行经验动态交互作用,雄性个体和雌性个体都具有最佳位置 p b e s t pbest pbest。
(1)雄性蜉蝣的更新
雄性蜉蝣容易成群聚集,每只雄性蜉蝣的位置是根据自身和邻近经验来调节的。设 x i t x_i^t xit是在第 t t t次迭代时蜉蝣 i i i搜索空间的当前位置,位置更新是第 t + 1 t+1 t+1次的迭代速度 v i t + 1 v_i^{t+1} vit+1加上第 t t t次迭代的位置之和,其位置表达式为: x i t + 1 = x i t + v i t + 1 (1) x_i^{t+1}=x_i^t+v_i^{t+1}\tag{1} xit+1=xit+vit+1(1)考虑到蜉蝣的不断移动,在水面上的一定距离内表演舞蹈,其速度更新为: v i j t + 1 = v i j t + a 1 e − β r p 2 ( p b e s t i j − x i j t ) + a 2 e − β r g 2 ( g b e s t j − x i j t ) (2) v_{ij}^{t+1}=v_{ij}^t+a_1e^{-\beta r_p^2}(pbest_{ij}-x_{ij}^t)+a_2e^{-\beta r_g^2}(gbest_j-x_{ij}^t)\tag{2} vijt+1=vijt+a1e−βrp2(pbestij−xijt)+a2e−βrg2(gbestj−xijt)(2)其中, v i j t v_{ij}^t vijt是蜉蝣 i i i在第 j j j维上第 t t t次迭代的速度; x i j t x_{ij}^t xijt是蜉蝣 i i i在第 j j j维上第 t t t次迭代的位置; a 1 a_1 a1和 a 2 a_2 a2是蜉蝣游动行为的吸引系数; p b e s t pbest pbest是个体的最佳位置; g b e s t gbest gbest是全局最优位置; β \beta β是能见度系数,用于控制蜉蝣的能见范围; r p r_p rp表示当前位置与 p b e s t pbest pbest的距离; r g r_g rg表示当前位置与 g b e s t gbest gbest的距离。其距离计算公式为: ∣ ∣ x i − X i ∣ ∣ = ∑ j = 1 n ( x i j − X i j ) 2 (3) ||x_i-X_i||=\sqrt{\sum_{j=1}^n(x_{ij}-X_{ij})^2}\tag{3} ∣∣xi−Xi∣∣=j=1∑n(xij−Xij)2(3)为了得到最优位置,蜉蝣必须要不断更新它的速度,其速度更新为: v i j t + 1 = v i j t + d × r (4) v_{ij}^{t+1}=v_{ij}^t+d\times r\tag{4} vijt+1=vijt+d×r(4)其中, d d d代表舞蹈系数,不断吸引异性; r ∈ [ − 1 , 1 ] r\in[-1,1] r∈[−1,1]是一个随机数。
(2)雌性蜉蝣的更新
雌性蜉蝣相比于雄性蜉蝣不同的地方是,雄性蜉蝣容易聚集而雌性蜉蝣不会群体聚集,但是雌性蜉蝣会飞来与雄性蜉蝣交配繁殖。假设 y i t y_i^t yit为雌性蜉蝣在第 t t t次迭代蜉蝣 i i i的位置,其位置更新表示为: y i t + 1 = y i t + v i t + 1 (5) y_i^{t+1}=y_i^t+v_i^{t+1}\tag{5} yit+1=yit+vit+1(5)雌性蜉蝣的速度更新如下: v i j t + 1 = { v i j t + a 2 e − β r m 2 ( x i j t − y i j t ) if f ( y i ) > f ( x i ) v i j t + f l × r else (6) v_{ij}^{t+1}=\begin{dcases}v_{ij}^t+a_2e^{-\beta r_m^2}(x_{ij}^t-y_{ij}^t)\quad \text{if}\,\,f(y_i)>f(x_i)\\v_{ij}^t+fl\times r\quad\quad\quad\quad\quad\quad\text{else}\end{dcases}\tag{6} vijt+1={vijt+a2e−βrm2(xijt−yijt)iff(yi)>f(xi)vijt+fl×relse(6)其中, v i j t v_{ij}^t vijt为蜉蝣的速度; y i j t y_{ij}^t yijt表示雌性蜉蝣 i i i在第 t t t次迭代的第 j j j维位置; a 2 a_2 a2表示吸引系数; β \beta β为能见度系数; r m r_m rm表示雄性和雌性蜉蝣的距离; f l fl fl是随机游走系数,只有在雌性蜉蝣在没有受到攻击时起作用; r ∈ [ − 1 , 1 ] r\in[-1,1] r∈[−1,1]是一个随机数。
(3)蜉蝣的交配过程
雄雌个体交配是生物自身的特点,蜉蝣亦是如此。其交配过程为:分别从雌性和雄性中选择一个亲本,选择雌雄样本的方式与雄性吸引雌性相同。选择过程是随机的,在该算法中,雄性蜉蝣的最优个体与雌性蜉蝣最优个体进行交配,雄性蜉蝣的次优个体与雌性蜉蝣的次优个体进行交配,交配后得到最优和次优的两个子代,其子代为: o f f s p r i n g 1 = L × m a l e + ( 1 − L ) × f e m a l e o f f s p r i n g 2 = L × f e m a l e + ( 1 − L ) × m a l e (7) \begin{aligned}&offspring1=L\times male+(1-L)\times female\\&offspring2=L\times female+(1-L)\times male\end{aligned}\tag{7} offspring1=L×male+(1−L)×femaleoffspring2=L×female+(1−L)×male(7)其中, L ∈ [ − 1 , 1 ] L\in[-1,1] L∈[−1,1]是一个随机数; m a l e male male是父本; f e m a l e female female是母本。
2、MA算法伪代码
二、仿真实验与结果分析
1、函数测试与数值分析
将MA与PSO和DE进行对比,以文献[1]中的F1、F7(单峰函数/30维)、F11、F12(多峰函数/30维)、CEC2017中的F7和F8(30维)为例,种群规模设置为40,其中雄性蜉蝣和雌性蜉蝣个体数量均为20,最大迭代次数设置为1000,每个算法独立运算30次。结果显示如下:



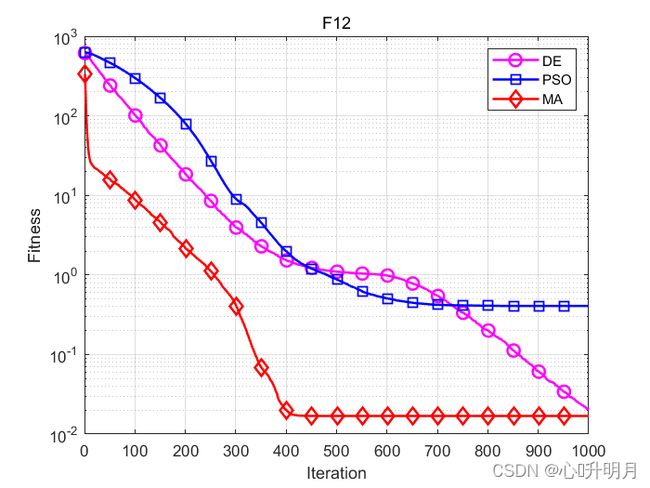
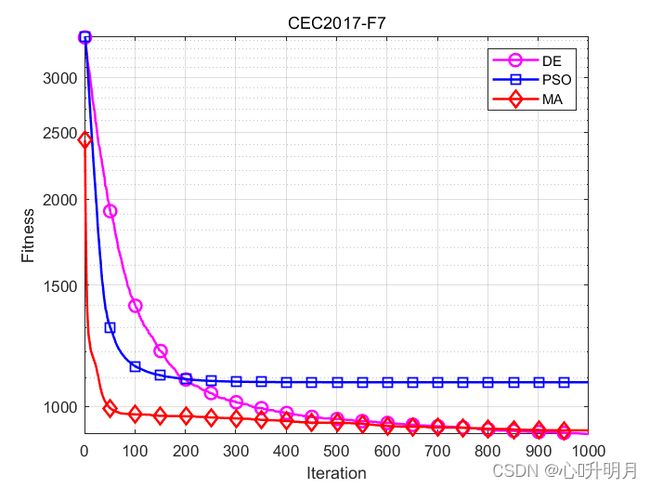
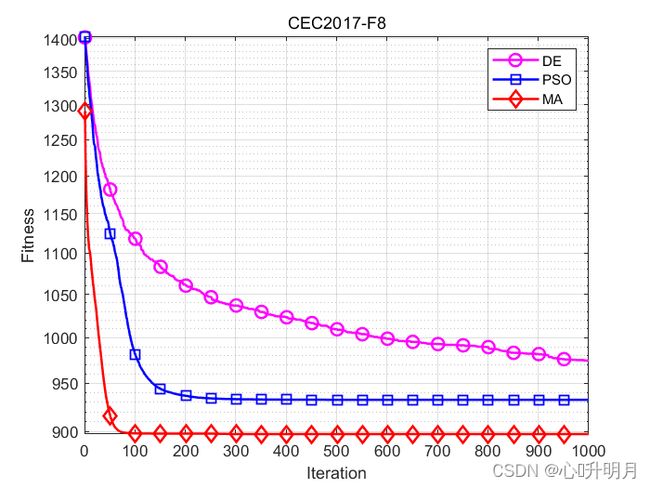
函数:F1
DE:最差值: 0.0032661, 最优值: 0.0008543, 平均值: 0.0017847, 标准差: 0.00065048
PSO:最差值: 1.6935, 最优值: 0.12447, 平均值: 0.62101, 标准差: 0.40203
MA:最差值: 3.6821e-17, 最优值: 1.6635e-23, 平均值: 2.1219e-18, 标准差: 7.9175e-18
函数:F7
DE:最差值: 25.1432, 最优值: 17.6081, 平均值: 21.8799, 标准差: 2.0529
PSO:最差值: 8.1848, 最优值: 1.724, 平均值: 4.0547, 标准差: 1.6994
MA:最差值: 1.0411, 最优值: 0.1826, 平均值: 0.55301, 标准差: 0.22589
函数:F11
DE:最差值: 5.3704, 最优值: 0.0088248, 平均值: 0.76023, 标准差: 1.4179
PSO:最差值: 7.4994, 最优值: 2.6567, 平均值: 4.1153, 标准差: 1.0085
MA:最差值: 2.8139, 最优值: 1.3404, 平均值: 2.0232, 标准差: 0.40594
函数:F12
DE:最差值: 0.036733, 最优值: 0.0059973, 平均值: 0.020133, 标准差: 0.0082632
PSO:最差值: 0.75997, 最优值: 0.15706, 平均值: 0.40747, 标准差: 0.11719
MA:最差值: 0.076015, 最优值: 0, 平均值: 0.016888, 标准差: 0.01797
函数:CEC2017-F7
DE:最差值: 926.012, 最优值: 887.3775, 平均值: 912.1119, 标准差: 10.7688
PSO:最差值: 1304.6903, 最优值: 933.4075, 平均值: 1084.5066, 标准差: 76.6244
MA:最差值: 1007.0842, 最优值: 844.5252, 平均值: 922.938, 标准差: 40.1233
函数:CEC2017-F8
DE:最差值: 996.1735, 最优值: 951.6529, 平均值: 974.7531, 标准差: 11.5671
PSO:最差值: 995.3236, 最优值: 893.0363, 平均值: 932.569, 标准差: 25.1225
MA:最差值: 927.3543, 最优值: 852.7328, 平均值: 897.2536, 标准差: 19.794
实验结果表明:MA在求解精度、收敛速度和寻优能力方面具有优越性。
2、WSN三维覆盖优化
节点覆盖模型请参考这里。设监测区域为 50 m × 50 m × 50 m 50m×50m\times 50m 50m×50m×50m的三维空间,传感器节点个数 N = 30 N=30 N=30,其感知半径是 R s = 10 m R_s=10m Rs=10m,通信半径 R c = 20 m R_c=20m Rc=20m,迭代500次。初始部署、MA优化覆盖、MA算法覆盖率进化曲线如下图所示。
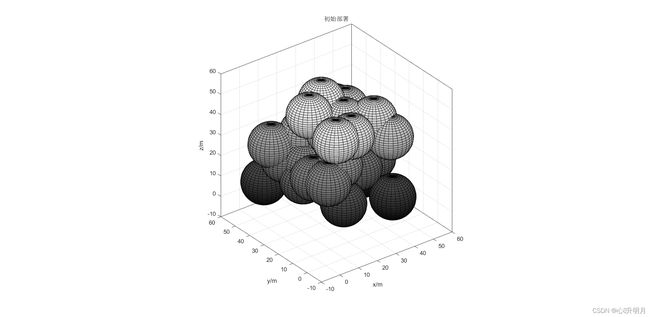


初始部署和最终部署的节点位置及对应的覆盖率分别为:
初始位置:
34.8741 31.5787 40.2763
7.6183 18.4415 21.967
16.1848 8.5948 10.7645
17.0297 12.537 27.4265
6.8927 1.821 48.0999
18.4442 21.7391 39.482
6.4694 37.3613 22.7609
26.7138 49.7516 8.074
32.0813 18.5512 18.3754
41.1463 36.9434 20.6148
8.4107 9.2335 23.2733
41.9088 30.3088 5.9463
26.4022 42.6506 26.4875
4.3673 48.5913 7.404
9.5253 23.8253 49.3932
14.6323 35.1682 34.0621
40.6422 6.2028 6.6426
10.9328 28.44 23.3253
41.0766 47.1676 31.7681
16.4521 3.6781 46.0263
34.2069 11.0143 44.8117
31.3838 26.3089 15.05
7.9709 26.1095 16.8307
20.9863 23.3088 11.4509
37.1923 3.4968 38.6245
20.6582 29.9993 49.9389
1.3724 39.7236 30.6272
23.9515 18.7036 44.197
42.7987 23.0489 17.4621
20.446 27.7723 34.7323
初始覆盖率:0.59216
最优位置:
27.8125 43.1955 27.4147
23.5183 4.9741 40.7511
40.7578 44.2315 42.5812
42.038 8.3549 7.6951
7.3799 43.0238 42.6001
33.6089 7.2945 23.7581
31.6978 24.8064 29.505
16.0765 6.7257 23.912
42.2437 43.5006 9.7819
5.0139 15.4829 24.8613
5.1741 31.8255 23.8061
42.3092 26.4937 14.1873
45.4135 18.1127 29.2397
9.6469 42.9547 26.3061
28.8598 35.7651 6.1156
6.829 6.9931 8.5318
6.8717 8.4658 41.8043
8.9398 22.4638 8.57
25.733 19.3137 45.3156
23.1844 36.4555 42.2754
28.1084 20.0536 7.9849
8.2334 40.9004 7.8439
6.608 26.598 41.8261
23.3935 6.3086 7.7337
41.9352 28.5294 43.3371
15.9941 19.5321 33.1469
40.9357 8.5794 41.8249
23.3137 44.4503 12.1368
43.2774 39.3243 27.2724
19.7363 27.4513 20.1312
最优覆盖率:0.80116
实验结果表明:MA算法能够提升三维无线传感器网络中节点部署的覆盖率。
三、参考文献
[1] Konstantinos Zervoudakis, Stelios Tsafarakis. A mayfly optimization algorithm[J]. Computers & Industrial Engineering, 2020, 145: 106559.
[2] 王义, 张达敏, 张琳娜, 等. 基于黄金正弦与自适应融合的蜉蝣优化算法[J]. 计算机应用研究, 2021, 38(10): 3072-3077.
