关联规则分析

一、经典案例

• 在美国，一些年轻的父亲下班后经常要到超市去买婴儿尿布，超市也因此发现了一个规律，在购买婴儿尿布的年轻父亲们中，有30%～40%的人同时要买一些啤酒。超市随后调整了货架的摆放，把尿布和啤酒放在一起，明显增加了销售额。如图1所示。
• 若两个或多个变量的取值之间存在某种规律性，就称为关联。
• 关联规则是寻找在同一个事件中出现的不同项的相关性，比如在一次购买活动中所买不同商品的相关性。
• 例如：“在购买计算机的顾客中，有20%的人也同时购买了打印机。”
  

图1 购买尿布和啤酒的关联规则集合

二、相关概念

图2为一个实例。

图2 关联规则实例

• 一个样本称为一个“事务”
• 每个事务由多个属性来确定，这里的属性称为“项”
• 多个项组成的集合称为“项集”

由k个项构成的集合

• {牛奶}、{花生酱}都是1-项集；
• {牛奶, 啤酒}是2-项集；
• {啤酒, 面包, 牛奶}是3-项集

X=>Y含义

• X和Y是项集
• X称为规则前项(antecedent)
• Y称为规则后项(consequent)

事务仅包含其涉及到的项目，而不包含项目的具体信息

• 在超级市场的关联规则挖掘问题中事务是顾客一次购物所购买的商品，但事务中并不包含这些商品的具体信息，如商品的数量、价格等。

支持度 (support)

• 一个项集或者规则在所有事务中出现的频率。$\sigma (X)$:表示项集$X$的支持度计数
• 项集$X$的支持度：$s(X)=\sigma (X)/N$
• 规则$X=>Y$表示项集$X$对项集$Y$的支持度，也就是项集$X$和项集$Y$同时出现的概率
• 某天共有100个顾客到电脑城购买物品，其中有20个顾客同时购买了计算机和打印机，那么上述的关联规则的支持度就是20%

置信度 (confidence)

• 确定$Y$在包含$X$的事务中出现的频率，即：$c(X=>Y)=\sigma (X\cup Y)/\sigma (X)$
• $P(Y|X)＝P(XY)/P(X)$
• 置信度反应了关联规则的可信度，即购买了项集$X$中的商品的顾客同时也购买了$Y$中商品的可能性有多大
• 购买咖啡的顾客中有50%的人购买了茶叶，则置信度为50%

如图3所示，规则$(A,B)=>C$：

• 支持度：交易中包含$\{A,B,C\}$的可能性 (25%)
• 置信度：在$\{A,B\}$交易的前提下包含$C$的条件概率 (100%)
  

图3

设最小支持度为50%, 最小可信度为 50%, 则可得到 :

• $A=>C$ (50%, 66.6%)
• $C=>A$ (50%, 100%)

若关联规则$X=>Y$的支持度和置信度分别大于或等于用户指定的最小支持度$minsupport$和最小置信度$minconfidence$，则称关联规则$X=>Y$为强关联规则，否则称关联规则$X=>Y$为弱关联规则。

提升度 (lift)

• $lift(A=>B)=confidence(A=>B)/support(B)=P(B|A)/P(B)$
• 现在有1000 个消费者，有500人购买了茶叶，其中有400人同时购买了咖啡，另100人没有。由于confidence(茶叶=>咖啡)=450/500=80%，由此可能会认为喜欢喝茶的人往往喜欢喝咖啡。但如果另外没有购买茶叶的500人，其中同样有400人购买了咖啡，同样是很高的置信度80%,由此，得到不爱喝茶的也爱喝咖啡。这样看来，其实是否购买咖啡，与有没有购买茶叶并没有关联，两者是相互独立的，其提升度为90%/[(450+450)/1000]=1 。

由此可见，$lift$正是弥补了$confidence$的这一缺陷，如果$lift=1$，则$X$与$Y$独立，$X$对$Y$出现的可能性没有提升作用，其值越大$(lift>1)$，则表明$X$对$Y$的提升程度越大，也表明关联性越强。
图4为一实例，可以看出，$X$对$Y$的提升作用最大。

图4

三、实验分析

自制数据集

可以使用mlxtend工具包得出频繁项集与规则，导包如下：

import pandas as pd
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules

自定义一份购物数据集，即：

retail_shopping_basket = {'ID':[1,2,3,4,5,6],
                         'Basket':[['Beer', 'Diaper', 'Pretzels', 'Chips', 'Aspirin'],
                                   ['Diaper', 'Beer', 'Chips', 'Lotion', 'Juice', 'BabyFood', 'Milk'],
                                   ['Soda', 'Chips', 'Milk'],
                                   ['Soup', 'Beer', 'Diaper', 'Milk', 'IceCream'],
                                   ['Soda', 'Coffee', 'Milk', 'Bread'],
                                   ['Beer', 'Chips']]
}

展示一下：

retail = pd.DataFrame(retail_shopping_basket)
pd.options.display.max_colwidth=100
retail

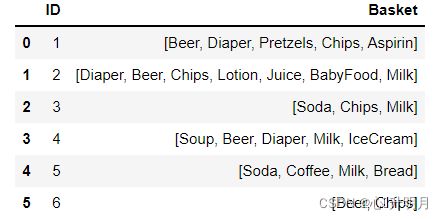
需要将现实数据转换成one-hot编码格式。
首先，剔除无关特征。

retail_id = retail.drop('Basket',1)
retail_id

显示如下：

其次，使用join()方法将列表改成字符串：

retail_Basket = retail['Basket'].str.join(',')
retail_Basket

然后，利用get_dummies()将分类变量转换为虚拟/指示符变量：

retail_Basket = retail_Basket.str.get_dummies(',')
retail_Basket

最后，将无关特征加进来即可：

retail = retail_id.join(retail_Basket)
retail

计算该数据集的支持度：

frequent_itemsets = apriori(retail.drop('ID',1), use_colnames=True)
frequent_itemsets

如果光考虑支持度support(X>Y)，[Beer, Chips]和[Beer, Diaper]一样，哪一种组合更相关呢？因此，需要计算提升度：

association_rules(frequent_itemsets,metric='lift')

显然{Diaper, Beer}更相关一些

电影数据集题材

数据集来源：https://grouplens.org/datasets/movielens/
查看该数据集前10项内容，显示如下：

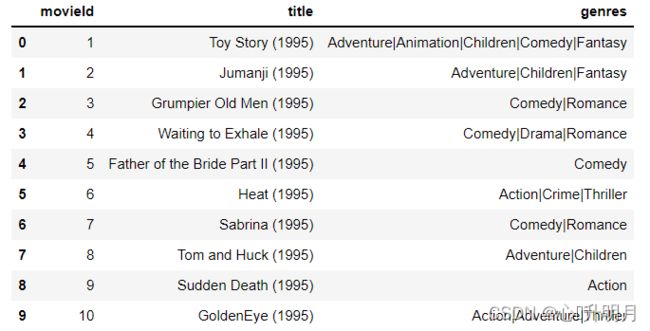
数据集中包括电影名字与电影类型的标签，第一步还是先转换成one-hot格式，并把无关特征设置为索引：

movies_ohe = movies.drop('genres',1).join(movies.genres.str.get_dummies('|'))
movies_ohe.set_index(['movieId','title'],inplace=True)
pd.options.display.max_columns=100
movies_ohe.head()

部分显示如下：

movies_ohe.shape

(9125, 20)，说明数据集包括9125部电影，一共有20种不同类型。
计算支持度大于0.015的频繁项集：

frequent_itemsets_movies = apriori(movies_ohe,min_support=0.015,use_colnames=True)
frequent_itemsets_movies

计算提升度大于1.25的项集：

rules_movies = association_rules(frequent_itemsets_movies,metric='lift',min_threshold=1.25)
rules_movies

计算提升度大于8的强关联项集，并按提升度值降序排列：

rules_movies[(rules_movies['lift']>8)].sort_values(by=['lift'], ascending=False)

这说明Children和Animation这两个题材是最相关的。
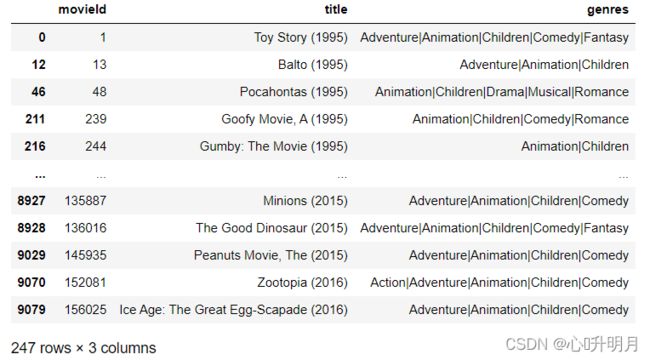
把包括{Children, Animation}的电影数据显示出来：

movies[(movies.genres.str.contains('Children')) & (movies.genres.str.contains('Animation'))]