GAN（对抗生成网络）原理及数学推导

本文主要涉及GAN网络的直观理解和其背后的数学原理。
参考课程：
计算机视觉与深度学习 北京邮电大学 鲁鹏

概述

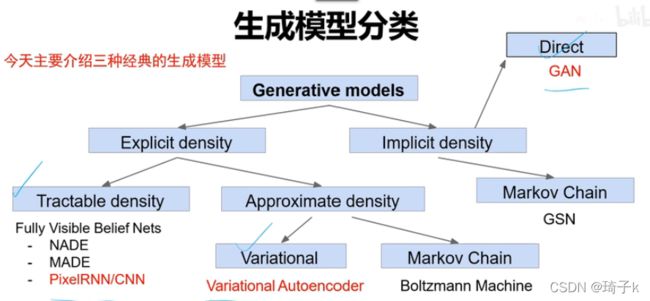
在所有生成模型中，GAN属于 “密度函数未知，直接硬train” 的那一类，和密度函数可定义的PixelRNN/CNN以及变分自编码器VAE有本质区别。

假设现在我们想做人脸的生成任务。我们希望能找到人脸图像的真实分布，这样直接在这个分布上随便取点，得到的都是人脸的图像。但是分布非常复杂，且无法知道。

所以，我们考虑用一个简单的分布和一个映射，将这个简单的分布映射到真实的分布。我们使用神经网络来学习这个映射的过程。

GAN的直观理解

目标函数

GAN网络的设计思路类似玩家博弈的过程，其主要优化的目标为：

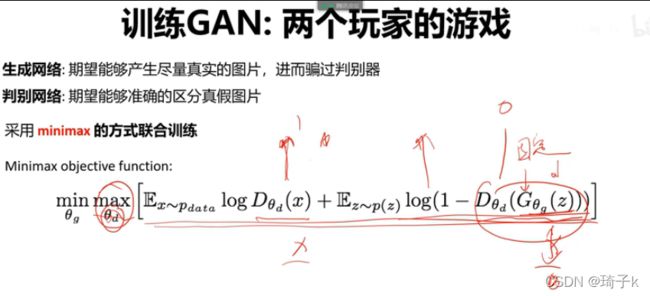
符号说明：P_data是真实数据的分布，P(z)是噪声分布(可以是均匀分布、高斯分布等)， theta(g)是生成器的参数， theta(d)是判别器的参数。
公式中
$$\hat{x}=G_{\theta }{}_g(z)$$
表示生成器生成的样本，而

$$D_{\theta }{}_d(x)$$
输出一个0-1之间的数，表示判别器对输入的判断，1表示是真实数据，0表示是生成的数据。

我们先看内侧max,调整theta_d(判别器的参数),使得后面式子最大。对于真实样本（Ex~data那一项），希望判别器生成1；对假样本x_hat，希望D_theta(d)把他输出成0，这样1减去之后最大。

【注意！！在讨论max的时候调整d，此时生成器g的参数是固定的！！反之亦然。】

再来看min的时候，学的是生成器g的参数。此时，前面那一项无所谓（与g无关）。此时希望
$$D_{\theta }{}_d(G_{\theta }{}_g(z))$$
趋近于1，此时theta_d不变，我们 希望生成的样本被判别器判断成1. 也就是固定D的前提下，让G尽量欺骗D。

theta_d想让表达式越大越好，所以是梯度上升。

因为判别器最后输出是(0, 1)的值，所以最后一层是一个sigmoid. 想让正样本越大越好，负样本越小越好，可以用一个二分类交叉熵损失（BCE）监督。【这里体会到：“似然越大越好” 等价于 “交叉熵损失越小越好”，因为那个max里面是一个概率/似然。下文会详细说明。】

但是实际这样梯度会出现问题——

这样训练的效果很差。因为刚开始生成的烂，梯度还小，学不动；后来生成的好，不太需要变化了，梯度反而很大。
G+D是一个网络，D在G后面。优化的时候，是冻结一个，训练另一个。而梯度回传会首先经过D，再回传到G。

实际实现时，我们会将min换成max，使得梯度问题得以解决。

用下面这张图总结下GAN网络的学习过程。

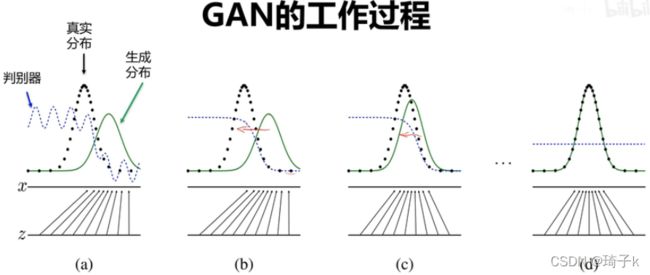
【这里(a)表示的意思是：一开始，判别器没有学好，无法区分真实和生成的分布。】

数学推导

JS散度

在开始之前，先给出JS散度的定义。
JS散度度量了两个概率分布的相似度，是基于KL散度的变体，解决了KL散度非对称的问题。一般地，JS散度是对称的，其取值是0到1之间。定义如下：

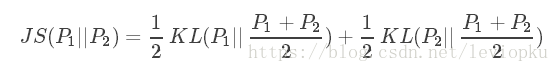
JS散度是可以理解为“距离”的，因为是对称的，而KL散度不行，只能说是一种“相似程度”。

极大似然估计 VS KL散度

一般的，我们要选取一个theta,使得似然值最大。

先放结论：

最大化似然 = 最小化KL散度。

【这是一个贯穿机器学习过程的关键理解】。

以下是每一步化简的过程：

回到GAN

Z是噪声服从的分布，这里可以取均匀分布或高斯分布。我们使用神经网络建模，学习了一个G，将Z映射到了一个密度分布P_G.
我们希望调整生成器的参数，使得G的密度分布与真实数据的密度分布接近（其中的Div表示散度，不一定是KL散度）。

但是，P_G是神经网络拟合的，Pdata是未知的，表达式我们根本写不出来，怎么优化？

以下是解决方法。
1、虽然我们不知道这两个分布的具体表达式，但是我们可以从中获取样本！

2、接着，我们把GAN的目标式子中的z统一换成G(因为样本是从G的分布里取出来的嘛)。

$$V(G,D)=E_{x-P_{data}}[logD(x)]+E_{x-P_G}[log(1-D(x))]$$
3、与上面类似，我们先考虑优化判别器（对应max的部分）。
这里先给出结论：

最大化maxV(D, G)等价于度量P_data和P_G之间的JS散度！

我们不是没法度量Div(Pg,Pdata)嘛？现在找到度量方式了！

只需要最大化V(D, G),便可以度量Pg和Pdata之间的JS散度。

先忽略结论的证明，我们绕开了Pdata和Pg数学表达式无法获得的问题，解决了度量两个密度分布的方法。因为maxV的时候，只需要把训练样本输入到神经网络中即可训练theta_G！

换言之，训练神经网络，实际就是在度量Pdata和Pg之间的JS散度。

直观理解

关于结论的证明，先从直观的角度来进行。

如果生成的和样本很像，判别器判别很困难，V（G,D）小【因为判断困难，真实数据得不到1，生成的假数据也得不到0，V值自然不高】；反之V（G，D）大 ==》 这不就类似在刻画“散度”嘛？

越好分，值越小，证明他们的距离越小；越难分，值越大，证明他们距离越大！

理论推导

这里用了一个结论：如果想要最大化积分，那么如果对于每个x，f(x)都是最大的，那积分出来的结果也最大，这样我们就去掉了积分符号。
在x给定的情况下，我们要找到最大的D’，对D求导即可。

将 前面求出的D’带入V(G, D), 并人为加入1/2的因子，朝着JS散度的方向化简。

最后我们便会发现，把最优参数带入后，此时的V(G, D)取到max值，也就是在度量Pdata与PG的JS散度。所以，判别器的输出值就代表了Pdata和Pg的差异！判别器输出值越大，表示Pdata和Pg分的越开；输出值越小，表示他们离得越近。

手动推导及每一步化简的过程：

再看目标式

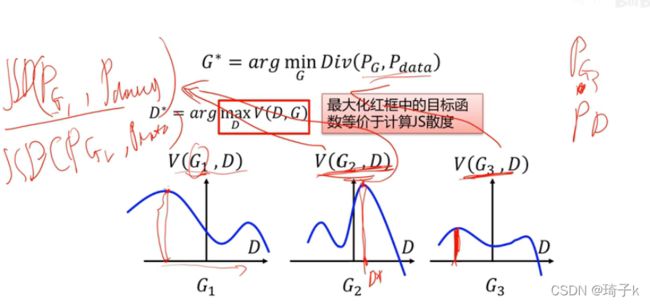
我们已经证明了，最大化V(D, G)就等价于计算了JS散度。所以对于上面的3个G，在固定G的情况下，我们可以得到D’为图中红色竖线的值(这时V最大)。
而生成器的优化目标为：找到一个最优参数G，使得生成的P_G的概率分布和真实数据的概率分布之间的差异越小越好。
假设我们现在G的候选参数就这三个，那就是从三个值里选择最小的值，G3就是最后学到的结果（因为他的V最小，而V是JS散度的刻画，生成器希望差异小）。

“判别器，最大化V(G, D)”可以理解为在蓝色的线上找最大值；
“生成器，最小化Div”可以理解为从所有红线中找出最小值。

而关键的桥梁“距离”，就是通过maxV(G, D）实现的。

实际操作

实际做的时候，可以用BCE做损失函数监督。【再次体现最大化似然等价最小化交叉熵】

Summary

但是其实GAN还是有很多问题的，这也是为什么后来出现了WGAN等，这个在这里就按下不表了。

一个小问题

在训练的过程中，我们往往对于判别器训练多次，而生成器只训练一次。这是为什么呢？
一个直观的理解是“判别器如果训练不好，那生成器训练多次也没什么用”，但这么理解只是流于表面。
可以从上面数学推导的理论来考虑。
优化D是为了是discriminator对应的目标函数最大，也就是在整个数据分布上，尽力做到正确区分，这个需要多轮过程做到，且优化D不会改变Pdata和Pg；但是对于generator，一次优化后，很可能此时此数据分布上的discriminator所最优的区分能力并不适合你已经改变之后的generator，导致不符合理论上的推导(也就是我们要最小化的JSD)【只有在固定D局部优化G时，才能看成近似优化两个分布的JS散度。 优化G之后，Pg已经变了，此时如果D不动而还训练G，就不符合理论了】。