作者:Grey
原文地址:二叉树的先,中,后序遍历
说明
本文主要介绍了二叉树的先序,中序,后序遍历。并且分别用如下三种方式实现:
- 递归方法
- 非递归(使用栈)
- Morris遍历方法,空间复杂度可以做到
O(1)
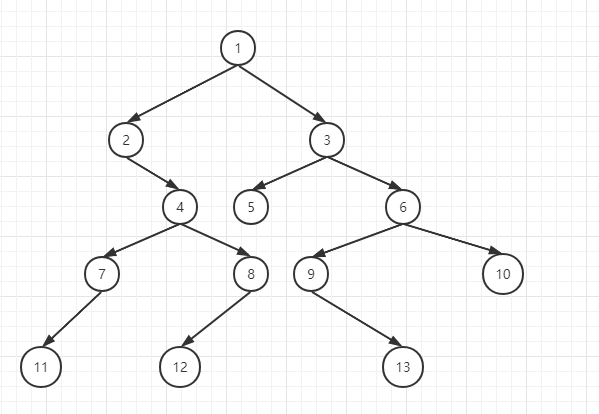
示例二叉树
数据结构
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
先序遍历
先序遍历流程
先头,再左,再右。
示例中的二叉树,先序遍历的结果为:
1-->2-->4-->7-->11-->8-->12-->3-->5-->6-->9-->13-->10
递归方法实现先序遍历
class Solution {
public static List preorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
p(root, ans);
return ans;
}
public static void p(TreeNode node, List ans) {
if (node == null) {
return;
}
ans.add(node.val);
p(node.left, ans);
p(node.right, ans);
}
}
使用栈实现先序遍历
整个流程是分如下几个步骤:
第一步,申请一个栈,并把头节点压入。
第二步,弹出就收集答案。
第三步,第二步中弹出的节点,如果右孩子不为空,则右孩子入栈。
第四步,第二步中弹出的节点,如果左孩子不为空,则左孩子入栈。
第五步,循环执行第二步到第四步,直到栈为空。
class Solution {
public static List preorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
if (root == null) {
return ans;
}
Stack stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode pop = stack.pop();
ans.add(pop.val);
if (pop.right != null) {
stack.push(pop.right);
}
if (pop.left != null) {
stack.push(pop.left);
}
}
return ans;
}
}
测评链接:LeetCode 144. Binary Tree Preorder Traversal
中序遍历
中序遍历流程
先中,再左,再右。
示例中的二叉树,中序遍历的结果为:
2-->11-->7-->4-->12-->8-->1-->5-->3-->9-->13-->6-->10
递归方法实现中序遍历
class Solution {
public List inorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
p(root, ans);
return ans;
}
public static void p(TreeNode root, List ans) {
if (root != null) {
p(root.left, ans);
ans.add(root.val);
p(root.right, ans);
}
}
}
使用栈实现中序遍历
也是申请一个栈,有如下几个步骤:
第一步,整条左边界入栈。
第二步,弹出就收集答案。
第三步,来到右树上执行同第一步的操作。
第四步,直到栈为空。
class Solution {
public List inorderTraversal(TreeNode head) {
List ans = new ArrayList<>();
if (head == null) {
return ans;
}
Stack stack = new Stack<>();
TreeNode cur = head;
while (!stack.isEmpty() || cur != null) {
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
TreeNode pop = stack.pop();
ans.add(pop.val);
cur = pop.right;
}
}
return ans;
}
}
测评链接:LeetCode 94. Binary Tree Inorder Traversal
后序遍历
后序遍历流程
先左,后右,再中。
示例中的二叉树,后序遍历的结果为:
11-->7-->12-->8-->4-->2-->5-->13-->9-->10-->6-->3-->1
递归方法实现后序遍历
class Solution {
public List postorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
p(root, ans);
return ans;
}
public static void p(TreeNode root, List ans) {
if (root != null) {
p(root.left, ans);
p(root.right, ans);
ans.add(root.val);
}
}
}
使用两个栈实现后序遍历
由于我们已经可以通过栈来实现先序遍历,即:先头,再左,再右。
而后序遍历的流程是:先左,再右,再头。
所以我们可以通过先序遍历的代码简单加工得到后序遍历的代码。
首先,我们先通过先序遍历的代码,将先序遍历加工成:先头,再右,再左。
把这个结果放入一个栈中,假设这个栈叫helper, 然后将helper中的内容依次弹出,便是后序遍历的结果。
class Solution {
public List postorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
if (root == null) {
return ans;
}
Stack stack = new Stack<>();
Stack helper = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode pop = stack.pop();
helper.push(pop);
if (pop.left != null) {
stack.push(pop.left);
}
if (pop.right != null) {
stack.push(pop.right);
}
}
while (!helper.isEmpty()) {
ans.add(helper.pop().val);
}
return ans;
}
}
测评链接:LeetCode 145. Binary Tree Postorder Traversal
Morris遍历
以上提到的二叉树的先,中,后序遍历算法,时间复杂度O(N),但是空间复杂度O(h),其中h是树的高度。Morris遍历也可以实现二叉树的先,中,后序遍历,且时间复杂度O(N), 空间复杂度可以做到O(1)。
Morris遍历流程
Morris遍历的流程主要分如下几个步骤:
第一步,从头节点开始遍历。
第二步,假设当前遍历的节点是cur。
第三步,如果cur无左树, cur来到其右树上,即:cur = cur.right
第四步,如果cur有左树,找到cur左树最右节点,假设叫mostRight,则有如下两种小情况:
情况1,如果mostRight的右指针指向空, 则将mostRight的右指针指向cur,即:mostRight.right = cur, 然后将cur向左移动,即:cur = cur.left,
情况2,如果mostRight的右指针指向当前节点cur,则将mostRight的右指针指向空,即:mostRight.right = null,然后将cur向右移动,即:cur = cur.right。
第五步:当cur = null,遍历结束。
代码实现如下:
// morris遍历
public class Code_0047_Morris {
public static void morris(TreeNode head) {
if (head == null) {
return;
}
// System.out.println("....morris order....");
TreeNode cur = head;
// System.out.print(cur.val + "-->");
TreeNode mostRight;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
// System.out.print(cur.val + "-->");
continue;
} else {
mostRight.right = null;
}
}
cur = cur.right;
// if (cur != null) {
// System.out.print(cur.val + "-->");
// }
}
}
}
根据如上流程,示例二叉树的Morris遍历序列为:
1-->2-->4-->7-->11-->7-->4-->8-->12-->8-->1-->3-->5-->3-->6-->9-->13-->6-->10
Morris遍历可以实现在O(N)时间复杂度内,用O(1)的空间复杂度实现对树的遍历,而且,只要某个节点有右树,则这个节点一定会被遍历两次,我们可以通过Morris遍历来实现二叉树的先,中,后序遍历,做到时间复杂度O(N),空间复杂度O(1)。
Morris遍历实现先序遍历
根据Morris的遍历结果,没有右树的点只会遍历一次,有右树的点会遍历两次,针对遍历一次的点,遍历到就收集,针对遍历两次的点,第一次遍历到就收集,第二次遍历到不收集,整个流程跑完,则得到了先序遍历的结果。
代码如下:
class Solution {
public static List preorderTraversal(TreeNode root) {
List ans = new ArrayList<>();
if (root == null) {
return ans;
}
TreeNode mostRight;
TreeNode cur = root;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
// 来到自己两次的点,在第一次来到自己就收集!!!!
ans.add(cur.val);
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
} else {
// 只来到自己一次的点,来到就收集。
ans.add(cur.val);
}
cur = cur.right;
}
return ans;
}
}
测评链接:LeetCode 144. Binary Tree Preorder Traversal
Morris遍历实现中序遍历
针对遍历一次的点,遍历到就收集,针对遍历两次的点,第一次遍历到不收集,第二次遍历才收集,整个流程跑完,则得到了中序遍历的结果。
代码如下:
class Solution {
public List inorderTraversal(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
List ans = new ArrayList<>();
TreeNode mostRight;
TreeNode cur = root;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
// 来到自己两次的点,第二次来到才收集
ans.add(cur.val);
mostRight.right = null;
}
} else {
// 只来到自己一次的点,来到就收集
ans.add(cur.val);
}
cur = cur.right;
}
return ans;
}
}
测评链接:LeetCode 94. Binary Tree Inorder Traversal
Morris遍历实现后序遍历
Morris遍历实现后序遍历相对比较麻烦,处理时机只放在能回到自己两次的点,能回到自己两次的点在第二次回到自己的时刻,不打印它自己,而是逆序打印他左树的右边界, 整个遍历结束后,单独逆序打印整棵树的右边界,即得到了后序遍历的结果。
代码如下:
class Solution {
public List postorderTraversal(TreeNode head) {
List ans = new ArrayList<>();
if (null == head) {
return ans;
}
TreeNode cur = head;
TreeNode mostRight;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
// 有左树的点第二次到达自己的时候
mostRight.right = null;
collectLeftTreeRightEdge(cur.left, ans);
}
}
cur = cur.right;
}
collectLeftTreeRightEdge(head, ans);
return ans;
}
// 逆序收集左树的右边界
private static void collectLeftTreeRightEdge(TreeNode head, List ans) {
TreeNode tail = reverse(head);
TreeNode c = tail;
while (c != null) {
ans.add(c.val);
c = c.right;
}
reverse(tail);
}
public static TreeNode reverse(TreeNode node) {
TreeNode pre = null;
TreeNode cur = node;
while (cur != null) {
TreeNode t = cur.right;
cur.right = pre;
pre = cur;
cur = t;
}
return pre;
}
}
需要注意两点:
第一点,collectLeftTreeRightEdge方法即逆序收集左树的有边界,由于每个节点没有指向父的指针,所以,要实现逆序,需要针对右边界采用反转链表的方式。即reverse函数的逻辑。
第二点,在collectLeftTreeRightEdge方法调用完反转链表操作后,还要还原整个右边界。否则整棵树的指针就指乱了。
测评链接:LeetCode 145. Binary Tree Postorder Traversal
更多
算法和数据结构笔记
参考资料
算法和数据结构体系班-左程云