北邮——R语言数据分析

温故而知新

6.函数

6.5 自定义函数

1. 基本使用

> ce2fa <- function(ce){
+   fa <- 1.8 * ce + 32
+   return(fa)
+ }
> ce2fa(0)
[1] 32
> ce2fa(0:10)
 [1] 32.0 33.8 35.6 37.4 39.2 41.0 42.8 44.6 46.4 48.2 50.0
> ce2fa
function(ce){
  fa <- 1.8 * ce + 32
  return(fa)
}
<bytecode: 0x00000233228bbb90>

2. R中的参数
   2.1 位置参数

> frm <- function(name,frm="BUPT"){
 1.   cat(name,"is from", frm)
 2. }
> frm(name = "AXB",frm = "BJTU")
AXB is from BJTU
> frm("AXB","BJTU")
AXB is from BJTU
#因为有位置参数，所以上面二者是等价的。

2.2 名义参数

> frm <- function(name,frm="BUPT"){
+   cat(name,"is from", frm)
+ }
> frm(name = "AXB",frm = "BJTU")
AXB is from BJTU
> frm(frm = "BJTU",name = "AXB")
AXB is from BJTU
#因为为名义参数，当指定对应参数名时，位置不影响赋值。

2.3 特殊参数——[…] (任意参数)

> my_func <- function(...){
 1.   cat("The second arg is ", ..2)#第二个参数
 2.   dot_args <- list(...)#通过list来捕捉任意参数
 3.   message("\nThe sum is ",sum(dot_args[[1]],dot_args[[5]]))
 4. }
> my_func(1,"arg2",3,4,5,6,7,8)
The second arg is  arg2
The sum is 6

3. 函数的二元操作符——既为函数
   1）+、-、*、/、^、>、<-、:、[、"% %"、

# +
> 1+2
[1] 3
> "+"(1,2)#可以看作一个函数调用的过程
[1] 3
> 10^2
[1] 100
> "^"(10,2)
[1] 100
> 2>1
[1] TRUE
> ">"(2,1)
[1] TRUE
> new_var <- 3
> "<-"(n,3)
> n
[1] 3
> new_var
[1] 3
> 1:10
 [1]  1  2  3  4  5  6  7  8  9 10
> ":"(1,10)
 [1]  1  2  3  4  5  6  7  8  9 10
> "["(1:10,2)
[1] 2
> c(1,3,9) %in% 1:3
[1]  TRUE  TRUE FALSE
> "%ab2c%" <- function(a,b){
+   sqrt(sum(a^2,b^2))
+ }
> 3 %ab2c% 4
[1] 5

2) 管道操作符

> library(purrr)
> x <- c(17,28,17,12,15,12,49)
> x %>%
+   unique() %>%
+   sort()
[1] 12 15 17 28 49

6.6 泛型函数

  单一接口，根据接口接收对象的类（这里的类并不是指数据类型，而是指不同的标签）不同而分发到不同的方法中去。——接口函数+不同具体的分发函数

> interface <- function(x,y){
+   message("Single interface")
+   UseMethod("particular",y)
+ }
> particular.classA <- function(x,y){
+   message("Different behavior: classA")
+ }
> particular.classB <- function(x,y){
+   message("Different behavior: classB")
+ }
> particular.default <- function(x,y){
+   message("Different behavior: default")
+ }
> x <- 1:10
> y <- 2:4
> class(y) <- "classB"
> interface(x,y)
Single interface
Different behavior: classB
> class(y) <- NULL
> interface(x,y)
Single interface
Different behavior: default

1. 查看一个函数有多少种泛型函数

> methods("+")
[1] +.Date        +.gg*         +.glue*      
[4] +.POSIXt      +.vctrs_vctr*
see '?methods' for accessing help and source code

2. 定义自己的泛型函数

> "+.onlyFirst" <- function(a,b){
+   return(a[1]+b[1])
+ }
> a <- 1:5
> a + 6:10
[1]  7  9 11 13 15
> class(a) <- "onlyFirst"
> a + 6:10
[1] 7

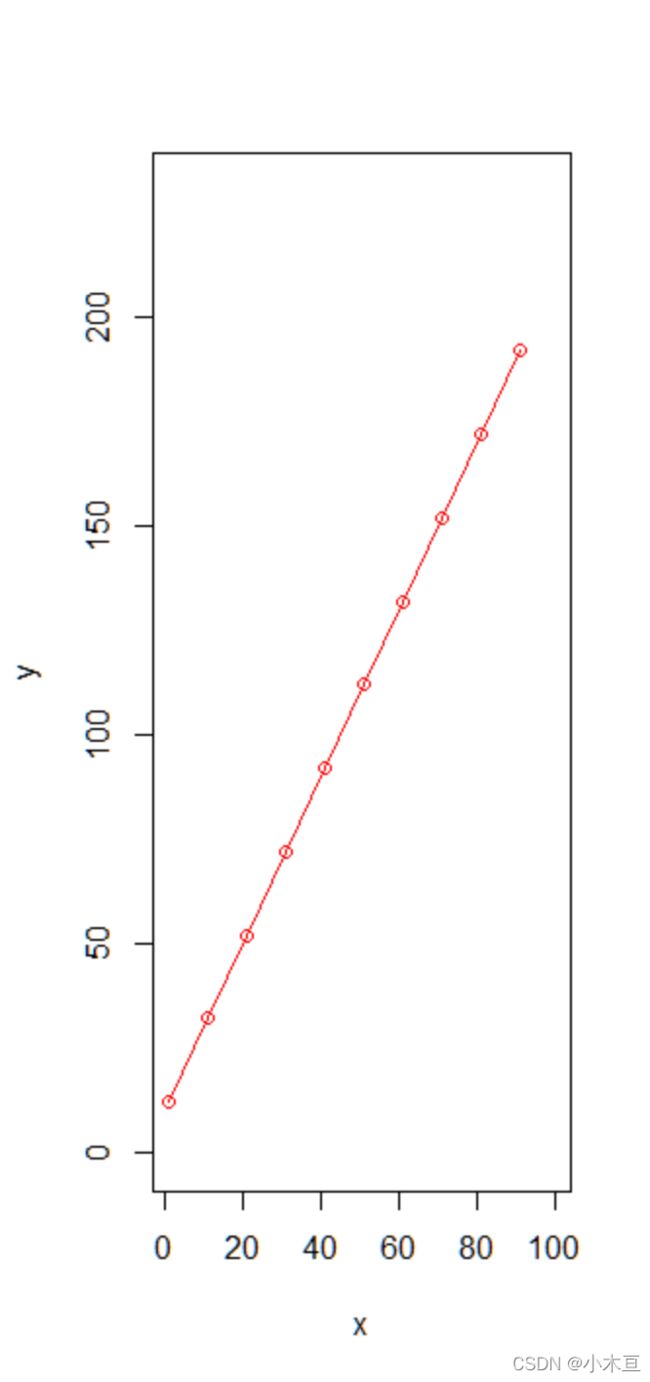
4. 数据矩阵绘图

> x <- seq(1,100,by=10)
> y <- 2*x + 10
> xy <- cbind(x,y)
> class(xy)
[1] "matrix" "array"
> plot(xy,
+   xlim = c(1,100),
+   ylim = c(0,230),
+   type = "o", col = "red")

6.7 递归——层层递进，逐层回归

> old_monk_story <- function(depth = 1){
+   message(rep(" ", depth),
+           "400 years ago(", 2018 - 400 * depth,
+           "), monk[", depth, "] is telling the story:")
+   if(2018 - 400 * (depth +1) >= 66){
+     old_monk_story(depth + 1)
+ }
+   message(rep(" ",depth),
+           "monk [",depth,"] finished his story")
+ }
> old_monk_story()
 400 years ago(1618), monk[1] is telling the story:
  400 years ago(1218), monk[2] is telling the story:
   400 years ago(818), monk[3] is telling the story:
    400 years ago(418), monk[4] is telling the story:
    monk [4] finished his story
   monk [3] finished his story
  monk [2] finished his story
 monk [1] finished his story

斐波那契数列——递归
1 2 3 5 8 13 21 34 55 …

> fib <- function(n){
+   if(n == 1){
+     return(1)
+   }
+     else {
+     return(c(fib(n-1),sum(tail(fib(n-1),n =2))))
+   }
+ }
> fib(10)
 [1]  1  1  2  3  5  8 13 21 34 55

7.数据对象（3组6类）

7.1 向量/因子

1. 向量

1.1向量类型

1.1 字符型向量
1.2 数值型向量
1.3 逻辑型向量

1.2 创建向量

2.1 创建向量时不能有类型混合，会进行强制类型转换
1）数值型—字符型
2）逻辑型—数值型（TRUE-1, FALSE-2）
2.2 不存在包含向量的向量，会对向量内部向量进行拆包
2.3 除了用c()可以创建向量，vector(), numeric(), logical()也可以创建指定类型的向量
2.4 创建有规则向量
1）等差序列

seq(from = , to = , by = )
seq(from = , to = , len = )

2）随机序列
1. 正态分布——rnorm()
2. 随机抽样——sample()
set.seed()——在这个条件下，随机生成的结果一样

1.3 访问向量子集

3.1 下标 [] —— 下标可重复，顺序可变
1）数值型下标
2）逻辑型下标——取出结果为TRUE的值
3）给向量中的元素起名，通过元素名访问子集

> xm
[1] "A" "B" "C" "D" "E" "F"
> yw
[1] 94 87 92 91 85 92
> names(yw) <- xm
> yw
 A  B  C  D  E  F 
94 87 92 91 85 92 
> yw[c("A","F")]
 A  F 
94 92

1.4 基本向量操作

4.1 排序
sort()——对向量直接排序
order()——返回排序下标
rev()——向量倒序

1.5 向量运算

在进行向量化运算时，若长度不等，则采取循环补齐的方式进行，1:10 - 1:3 相当于1:10 - c(1:3, 1:3, 1:3, 1)

2. 因子类型

向量——存储数值变量（定距定比）
因子——存储类别变量（定类定序）

2.1 因子的应用

（1）分组统计中，因子常用作分组变量
（2）分类问题，均要求因变量为因子
（3）在其它一些算法建模过程中，要求变量为因子（如apriori算法）

2.2 因子的创建与操作

2.1 基于向量

#分类但无序
> xb <- c("F","M","F","F")
> typeof(xb)
[1] "character"
> xb <- factor(xb)
> typeof(xb)
[1] "integer"#factor表面看是一个字符向量，其实是一个整型的数值向量
> mean(as.numeric(number_factors))
[1] 1.6
> as.numeric(number_factors)
[1] 1 2 2 2 1
> as.numeric(xb)
[1] 1 2 1 1
> as.character(xb)
[1] "F" "M" "F" "F"
> xb
[1] F M F F
Levels: F M
> nlevels(xb)
[1] 2
> levels(xb)
[1] "F" "M"

#分类但有序
> score <- factor(c("优","良","优","优","良","优"),**ordered**=TRUE)
> score[1] > score[2]
[1] TRUE#可以自动识别出优比良好
> days <- factor(c("MON","TUE","WED","THUR","FRI"),ordered = TRUE)
> days[3]<days[2]
[1] FALSE
> days[3] > days[2]
[1] TRUE
> days
[1] MON  TUE  WED  THUR FRI 
Levels: FRI < MON < THUR < TUE < WED #因子的识别是按照首字母的26个字母排序来的

2.2 数据分箱

#数据分箱+闭区间+左开右闭
> yw <- c(94,87,92,91,85,92)
> yw5 <- cut(yw,
+            breaks = c(0,(6:10)*10))
> yw5
[1] (90,100] (80,90]  (90,100] (90,100] (80,90]  (90,100]
Levels: (0,60] (60,70] (70,80] (80,90] (90,100]
#数据分箱+有序数据+左闭右开
> yw5 <- cut(yw,
+            breaks = c(0,(6:10)*10),
+            include.lowest = TRUE,
+            right = FALSE,
+            ordered_result = TRUE)
> yw5
[1] [90,100] [80,90)  [90,100] [90,100] [80,90)  [90,100]
Levels: [0,60) < [60,70) < [70,80) < [80,90) < [90,100]
#数据分箱+有序数据+左闭右开+标签
> yw5 <- cut(yw,
+            breaks = c(0,(6:10)*10),
+            include.lowest = TRUE,
+            right = FALSE,
+            ordered_result = TRUE,
+            labels = c("不及格","及格","中","良","优"))#标签需要和前面的levels一一对应
> yw5
[1] 优 良 优 优 良 优
Levels: 不及格 < 及格 < 中 < 良 < 优

7.2 矩阵/数组

1. 矩阵

1.1 矩阵的创建

> ysw <- matrix(c(94, 87, 92, 91, 85, 92,
+                 82, 94, 79, 84, 92, 82,
+                 96, 89, 86, 96, 82, 85),
+               ncol = 3)
> ysw#默认按照列的顺序来填充矩阵
     [,1] [,2] [,3]
[1,]   94   82   96
[2,]   87   94   89
[3,]   92   79   86
[4,]   91   84   96
[5,]   85   92   82
[6,]   92   82   85
> colnames(ysw) <- c("yw","sx","wy")
> row.names(ysw) <- xm
Error in dimnames(x) <- dn : 'dimnames'的长度[1]必需与陈列范围相等
> xm <- c("A","B","C","D","E","F")
> row.names(ysw) <- xm
> ysw
  yw sx wy
A 94 82 96
B 87 94 89
C 92 79 86
D 91 84 96
E 85 92 82
F 92 82 85
#设置按照行的顺序来填充矩阵
> ysw <- matrix(c(94, 87, 92, 91, 85, 92,
+                 82, 94, 79, 84, 92, 82,
+                 96, 89, 86, 96, 82, 85),
+               byrow = TRUE,
+               ncol = 3)
> colnames(ysw) <- c("yw","sx","wy")
> row.names(ysw) <- xm
> ysw
  yw sx wy
A 94 87 92
B 91 85 92
C 82 94 79
D 84 92 82
E 96 89 86
F 96 82 85

1.2 矩阵的基本性质

###矩阵基本属性
> colnames(ysw)#列名
[1] "yw" "sx" "wy"
> rownames(ysw)#行名
[1] "A" "B" "C" "D" "E" "F"
> dimnames(ysw)#行名+列名
[[1]]
[1] "A" "B" "C" "D" "E" "F"

[[2]]
[1] "yw" "sx" "wy"
> nrow(ysw)#行数
[1] 6
> ncol(ysw)#列数
[1] 3
> dim(ysw)#矩阵维度
[1] 6 3

###子集访问
##访问第一行
> ysw[1,]
yw sx wy 
94 87 92 
> ysw["A",]
yw sx wy 
94 87 92
##访问列
> ysw[,"sx"]
 A  B  C  D  E  F 
87 85 94 92 89 82 
> ysw[,2]
 A  B  C  D  E  F 
87 85 94 92 89 82
##去除第二列
> ysw
  yw sx wy
A 94 87 92
B 91 85 92
C 82 94 79
D 84 92 82
E 96 89 86
F 96 82 85
> ysw[,-2]
  yw wy
A 94 92
B 91 92
C 82 79
D 84 82
E 96 86
F 96 85

###行列重排
##列重排
> ysw[,c("sx","yw","wy")]
  sx yw wy
A 87 94 92
B 85 91 92
C 94 82 79
D 92 84 82
E 89 96 86
F 82 96 85
> ysw[,c(2,1,3)]
  sx yw wy
A 87 94 92
B 85 91 92
C 94 82 79
D 92 84 82
E 89 96 86
F 82 96 85
##行重排
#order()函数，排序并返回下标
> order_sx <- order(ysw[,"sx"],
+   decreasing = TRUE)
> ysw[order_sx,]
  yw sx wy
C 82 94 79
D 84 92 82
E 96 89 86
A 94 87 92
B 91 85 92
F 96 82 85

###矩阵合并
##行合并
rbind()
##列合并
cbind()
##当两个矩阵顺序不统一时，进行合并
tidyverse::merge
tidyverse::join

###矩阵运算
##求和
#行求和
rowSums()
#列求平均值
colMeans()
##对每一行/列循环操作
apply(matrix, 1/2, function)#1_row,2_column
apply家族的处理思路：split-apply-combine模式

1.3 矩阵运算

#利用矩阵解方程
> A <- matrix(
+     c(1, 2, 3,
+       2, 2, 5,
+       3, 5, 1),
+     ncol = 3,
+     byrow = TRUE)
> b <- 1:3
> solve(A,b)#求矩阵的逆
[1] 1 0 0
> solve(A) %*% A#A的逆矩阵 * A 得到的是单位矩阵
              [,1]          [,2]          [,3]
[1,]  1.000000e+00  8.881784e-16  1.054712e-15
[2,] -4.440892e-16  1.000000e+00 -7.077672e-16
[3,] -5.551115e-17 -1.110223e-16  1.000000e+00
> solve(A) %*% A %>% dplyr::near(.,diag(3))#dplyr::near()求近似值
     [,1] [,2] [,3]
[1,] TRUE TRUE TRUE
[2,] TRUE TRUE TRUE
[3,] TRUE TRUE TRUE
> all(near(solve(A) %*% A, diag(3)))
[1] TRUE

R中矩阵的基本操作

2.数组——高维矩阵（这里主要讲三维）

例1：导入图片——图片的操作本质上都是数组的操作

#载入需要的包
> library(magrittr)
> install.packages("imager")
> library(imager)
#创建对象，并加载图片
> presidents <- load.image("D:/R/R-4.0.5/R_Files/presidents.jpg")
#查看图片参数的数据类型
> str(presidents) %>% print
 'cimg' num [1:482, 1:345, 1, 1:3] 0.984 0.961 0.918 0.902 0.902 ...
##这是一个彩色图片，RGB（红、绿、蓝），可以看作一个三维数组
> presidents[, , 2] <- 0
> presidents[, , 3] <- 0
> plot(presidents)
##去除第三个图层，则只留下红色的图层

#给图片特定区域加马赛克
> area_coor_x <- 350:449#图片中需要马赛克的x坐标
> area_coor_y <- 110:259#图片中需要马赛克的y坐标
> array_dim <- c(length(area_coor_x),
+                length(area_coor_y),
+                3)
> array_data <- runif(prod(array_dim))#将各维度数据相称，并均质化
> random_noise <- array(dim = array_dim,
+                       data = array_data)#设置一个数组形式的随机噪音
> presidents[area_coor_x,area_coor_y,] <- 
+   (1 - 0.6) * presidents[area_coor_x,area_coor_y,] +
+   0.6 * random_noise#将这个随机噪音添加到原来的图片上，并给自己随机噪音设置系数，两个系数相加等于1即可
> plot(presidents)

7.3 数据框/列表

1.列表

1.1 list性质

（1）列表是对象的有序集合
（2）列表的对象可以是不同类型、不同长度
（3）列表最为灵活，最具包容性

1.2 list创建

list()

1.3 list访问

#1.LIST$NAME——得到的是一个向量
#2.LIST[]——得到的是一个列表（通用法则：子集X[]的类型与X相同）
   LIST[[]]——得到的是向量（[[]]）
#3.LIST$NAME、LIST[[]]、LIST[["NAME"]]——得到的效果一样

1.4 更改列表元素——总体为赋值

#1.直接重新赋值
#2.删除某个部分——将其赋值给NULL（tips：注意NA、NULL、”“之间的区别）

1.5 对列表的某一部分，执行相同的操作

lapply(LIST,FUNCTION)#返回的结果为list形式
sapply(LIST,FUNCTION)#返回的结果形式为向量

2.数据框

2.1数据框性质

（1）形式是矩阵，本质是列表
（2）列：变量、属性、特征、维度
行：记录、观测值、N维数据空间的一个点

2.2 数据框的创建

A <- data.frame()

2.3 数据框的访问

A$colName
A[row,col]
  #4种下标访问方式：
   1.正整数——选出
   2.负整数——排除 ##正整数和负整数做下标时，不能混用
   3.逻辑值——TRUE(选出)、FALSE(排除)
   4.名称字符串

2.4 更改数据框

#将数据框和新的一列组合起来
cbind()

2.5 读取数据框

A_url <- "地址"
read.csv()#如果读取时乱码，则在参数中加入encoding = "UTF-8"

2.6 查看数据框

#1.查看数据框
view()
head()
tail()
#2.查看数据框结构
str()
#3.对数据框进行统计描述
summary()#按照列进行统计
#4.查看数据框的基本属性
names()
colnames()
nrow()
ncol()
length()

2.7 更改数据框类型转换——本质为赋值

dataframe$NAME <- factor(dataframe$NAME)
#做完数据转换之后，再次进行summary

2.8 数据框记录排序

order()

2.9 训练集和测试集

#将一个数据框分为训练集和测试集（训练集和测试集一般7：3）
> set.seed(2021)
> n_record <- nrow(cjb)
> train_idx <- sample(1:n_record,floor(n_record * 0.7))#在数据框中随机选出70%的数据，并向下取整
> length(train_idx)
[1] 542
> test_idx <- setdiff(1:n_record,train_idx)#选出数据框中非训练集的部分，setdiff(A,B)存在于A中，但不在B中的数据
> length(test_idx)
[1] 233
#得到训练集和测试集
> train_set <- cjb[train_idx,]
> test_set <- cjb[test_idx,]

2.10 数据框与机器学习

（1）分类——数据框与函数
数据框本质就是函数中的列表法

（2）聚类
数据框具有N维属性/特性，组成一个N维的数据空间
距离关系的远近，在无监督学习的情况下，在数据空间中，自然形成了结构：簇
（3）关联规则
支持度
置信度

2.11 数据框的本质及其衍射

数据框—关系表

1. data.frame
2. tidyerse::tibble
3. data.table（当数据量大于1GB时，data.table处理效率高）
   数据框是R算法建模过程中，最常用的数据对象，其中蕴含各类关系结构，包括映射关系、距离关系、伴随关系、相关关系、拓扑关系等

7.4 数据材质

名称	类型	示例
逻辑型	logical	F,T
整型	integer	1L,300L
双精度型	numeric	1,3.14
复数型	complex	1+2i
字符型	character	“Hello,world”
原始字节数据	raw	b0

8.算法模型

8.1近邻法——kNN（k-最近邻分类），空间划分的角度

1.基本组成

#输入：最近邻数目—— k，训练集S，测试集T
#输出：对测试集T中所有的样本贴上相应的标签，预测其类编号值
(1)for每个测试样本 z = (X',y') ∈ T # X'_特征向量；y'_类标签
(2)   计算z和每个训练样本(X',y') ∈ S之间的距离d(X,X')
(3)	  选择离z最近的k最近邻集合Sz包含于S
(4)	  多数表决y' = argmax∑(xi,yi) ∈ Dz I(v = yi)
(5)end for
##距离d的计算
1.欧几里得距离
2.曼哈顿距离

1.2 weighted kNN_加权近邻法

（1）意义：近邻法会由于k的取值不同而产生不同的结果，这个时候使用加权法，给每个点加上一定比重，距离越近，比重越高。

wi即为这个权重，可以取不同的核函数，如高斯核，求距离的倒数

1.3 k值和核的确立

通过实验的方法，一步步尝试，看哪个值性能表现最好

1.4 近邻法R语言实现

>library(kknn)
#################################
##构建预测模型
> imodel <- kknn(wlfk ~ .,#构建因变量和自变量函数
+                 train = cjb[train_set_idx, ],#载入训练集
+                 test = cjb[train_set_idx, ])#将训练集当作测试集，来查看其拟合情况
> predicted_test <- imodel$fit#挑选出模型中查看拟合情况的部分
> Metrics::ce(cjb$wlfk[train_set_idx, ], predicted_test)#查看模型的分类错误率，分析其拟合效果
#> [1] 0.1107011
##再用测试集，来查看拟合情况（这时训练和测试同时进行）
> imodel <- kknn(wlfk ~ .,#构建因变量和自变量函数
+                 train = cjb[train_set_idx, ],#载入训练集
+                 test = cjb[-train_set_idx, ])#测试集，来查看其拟合情况
> predicted_test <- imodel$fit#挑选出imodel列表中fit模型中查看拟合情况的部分
> Metrics::ce(cjb$wlfk[-train_set_idx, ], predicted_test)#查看测试集的分类错误率，查看其泛化误差，分析其拟合效果
#> [1] 0.2586207
#################################
##选取合适的k值和核函数
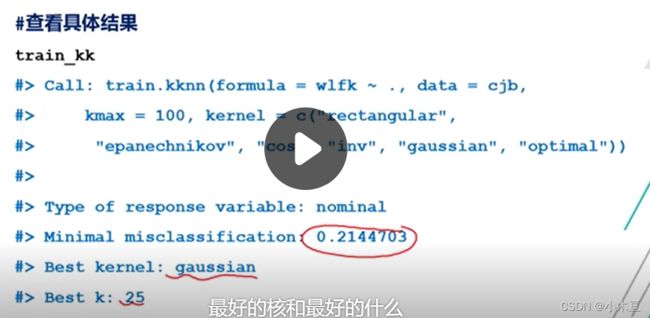
> train_kk <- train.kknn(
+   wlfk ~ .,
+   data = cjb,
+   kmax = 100,#最大k值
+   kernel = c(#在这么多核函数中进行选择
+     "rectangular","epanechnikov",
+     "cos","inv",
+     "gaussion","optimal"))
#得到了train_kk
#其中
best_k <- train_kk$best.parameters$k#最好的k值
best_kernel <- train_kk$best.parameters$kernel
####################################
#k折交叉检验
#1.目的：继续测试，使模型参数稳定在一定性能上
#2.方法：每一次1折为测试集，其余k-1折为训练集
> sp <-  Sys.time()
> cat("\n[Start at:", as.character(sp))

[Start at: 2021-12-26 16:12:30
> for (i in 1:lenth(kfolds)){
+   curr_fold <- kfolds[[i]]#取出当前这一折
+   train_set <- cjb[-curr_fold,]#k-1折为训练集
+   test_set <- cjb[curr_fold,]#当前这一折为测试集
+   predicted_train <- kknn(
+     wlfk ~ ., train = train_set, test = train_set,
+     k = best_k,kernal = best_kernel)$fit#查看训练集拟合效能表现
+   imerics("kknn","Train",predicted_train,train_set$wlfk)
    predicted_test <- kknn(
      wlkf ~ ., train = train_set,test = test_set,
      k = best_k, kernel = best_kernel)$fit
    imetrics("kknn","Test",predicted_test,test_set$wlfk)
    }
    ep <- Sys.time()
    cat(["\tFinished at:", as.character(ep),"]\n")
    cat("[Time Ellapsed:\t",
        difftime(ep,sp,units = "secs")," seconds]\n")

最好的k值：25
最好的核函数：gaussian
最小分类错误率：0.2144703

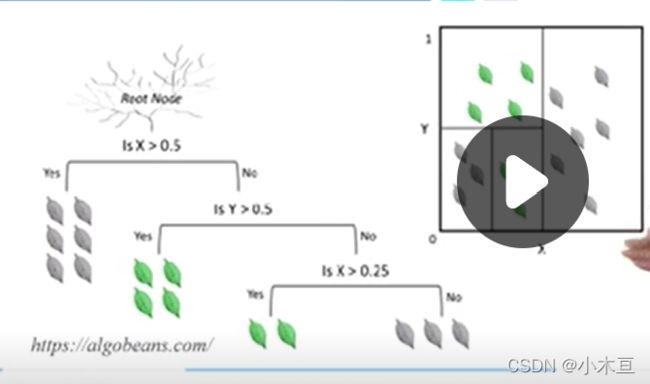
8.2 决策树

1.定义

  不断细分数据空间，纯化数据空间，从而实现分类

1.2 决策树中的一种——cart分类决策树[基尼系数]（决策树不同的算法是基于不同的纯度来划分的）

（1）工作原理
1.各种条件属性的组合，根据特征进行决策
2.局部最优，不断细化——当前特征属性的选择+取值范围的选择
（2）决策树归纳算法TreeGrowth(D，F)——递归

（3）代价—复杂度剪枝

		α：取值区间不同，对应的最优树不同

（4）寻找决策树
1.决策树的生成
2.根据代价-复杂度进行剪枝——设置不同的α取值区间，从而生成不同的决策树
2.将所有决策树序列进行交叉验证，查看泛化性能最佳的决策树

8.3 随机森林——属于分类器组合学习

1.1 定义

（1）集成学习
将多个弱分类器组合成一个强分类器
（2）流程
1.将数据集分成多个子集
1.1 利用重采样/有放回抽样的方法，各个子集之和会大于原始数据集
（随机森林过程中通过有放回的重采样方法，样本大小与原数据集大小一致，但有36%左右的数据不被抽到）
2.每个子集选取不同的特征属性，生成相应的弱分类器
3.利用弱分类器对测试集进行验证
4.采用不同的法则（如少数服从多数）来决定最终分类结果——生成强分类器

1.2 R语言实现（大致流程同前）

8.4朴素贝叶斯

1.定义

（1）抽象理解：通过条件概率来减少不确定性
（2）贝叶斯：

（3）朴素贝叶斯的本质：学到了先验概率和条件概率对结果的影响

8.5 logistic(逻辑斯蒂回归)

8.6 人工神经网络

1.1 基本结构

输入层—隐藏层—输出层

8.7 支持向量机

9.聚类——无监督学习

9.1 聚类形成的自然空间结构——簇（cluster）

1.1簇的类型

（1）明显分离的簇
（2）基于中心的簇
（3）基于邻近的簇
（4）基于密度的簇

9.2 聚类方法

1.1 基于划分的聚类方法——kMeans

（1）对象属性：簇内高相似性，簇间低相似性

1.2 层次聚类

（1）基本凝聚层次聚类算法
（2）