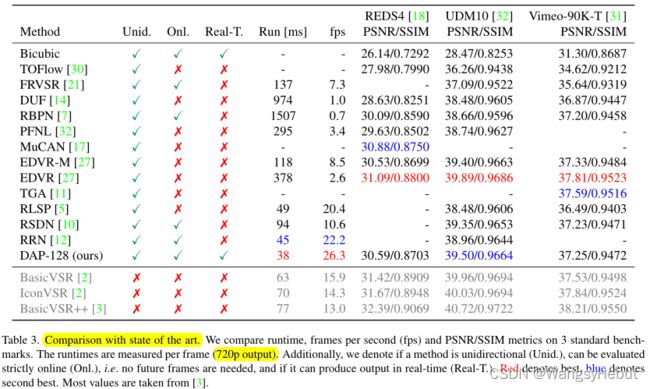
26FPS在线输出720P视频的视频超分模型：DAP

作者单位：苏黎世联邦理工、鲁汶大学、维尔兹堡大学
论文链接：https://arxiv.org/pdf/2202.01731v1.pdf
编者言：不同于现阶段VSR的两大热点研究方向：真实世界/盲VSR、VSR与传输，本文作者在实时在线领域超分方向实现突破，这与IPRRN一文的出发点类似。本文DAP的效果堪比EDVR，但是时间缩短了三倍，180P视频在线可达26FPS！

看点

VSR的应用具有严格的因果、实时等限制。这存在两个挑战：未来帧的信息不可用、设计高效且有效的帧对齐和融合模块。本文提出了一种基于可变形注意金字塔（DAP）的循环VSR结构。DAP将来自循环状态的信息对齐并整合到当前帧预测中。为了规避传统的基于注意的方法的计算成本，DAP只关注有限数量的空间位置，这些位置由DAP动态预测。 在两个基准上超过了EDVR-M方法，速度超过3倍。

方法

Overview

根据奈奎斯特-香农的采样定理，离散信号的频带被限制，VSR算法的任务是从低分辨率视频中恢复高于上述频率的高频内容。本文的递归算法重点强调快速运行时结合隐藏状态下信息的更新与提取来处理帧之间的对齐。首先，我们的编码器网络$\epsilon$将输入帧$x_t$与$x_t-1$编码为从细到粗的多级特征图，然后可变形注意模块迭代地将计算出的偏移量$s_t$从粗到细进行细化，然后融合模块根据最终偏移量聚合隐藏状态特征，最后由由多个残差信息蒸馏块组成的主要处理单元$N$估计高分辨率帧和下一个隐藏状态，框架如下图所示。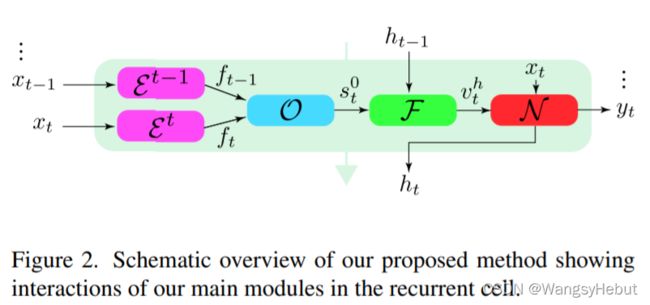

DAP

首先使用U-Net型编码器从$X_t$和$X_{t-1}$中计算多级特征。 在第$l$层金字塔，k个采样位置$s_t^l$被计算去充当上一层可变形注意模块的关键位置，在使用卷积块$C_S^l$去计算残差偏移量时的特征是根据$s_t^t+1$从t-1到t的交叉注意力融合而来的，偏移量$s_t^l$会反复优化，直到$l$=0，如下图所示，其中⊗代表通道叠加，⊕代表像素相加。

多级编码器

视频中的存在快速运动，本文设计了一个多级编码器以获得多分辨率的特征。由于不同分辨率帧上有不同的空间视图，这可以捕捉不同范围的运动。层级定义为$l(0L)$，本实验中L=3，并对不同时间的输入使用单独的处理链，特征计算如下：$$\begin{array}{rlrlrl}{f}_t^l& =D_{\downarrow }\left({\mathcal{C}}^l\left(f_t^{l-1}\right)\right),& f_t^0& ={\mathcal{C}}^0\left(x_t\right),& l& =0,\dots ,L\\ f_{t-1}^l& =D_{\downarrow }\left({\mathcal{C}}^l\left(f_{t-1}^{l-1}\right)\right),& f_{t-1}^0& ={\mathcal{C}}^0\left(x_{t-1}\right),& l& =0,\dots ,L\end{array}$$其中$C^l$表示由4个卷积组成的卷积块，$D_{\downarrow }(\cdot )$表示双线性下采样。

可变形注意

为了降低注意力模块的复杂度，本文将显著特征的搜索限制在特征图中动态选择的位置，而不是在一个大的邻域甚至整个帧上进行相关的穷举计算。 通过仅计算密集像素的相关性，大大减少了计算工作量。其中$Q_t^l$为当前帧的特征表示，$K_{t-1}^l$和$V_{t-1}^l$由动态预测空间位置$s^l$和$f_{t-1}$计算。计算如下：$$\begin{array}{rl}l& =L,\dots ,0\\ Q_t^l& =W_Q^l{f}_t^l\\ K_{t-1}^l& =W_K^l\mathcal{S}\left(f_{t-1}^l,U_{\uparrow }\left(s_t^{l+1}\right)\right)\\ V_{t-1}^l& =W_V^l\mathcal{S}\left(f_{t-1}^l,U_{\uparrow }\left(s_t^{l+1}\right)\right)\\ v_t^l\left(Q_t^l,K_{t-1}^l,V_{t-1}^l\right)& =\mathrm{softmax}\left(\frac{Q_t^l{K}_{t-1}^{l^T}}{\text{ c }\sqrt{\text{ id }}}\right)V_{t-1}^l\end{array}$$其中$U_{\uparrow }(\cdot )$表示双线性上采样。

迭代细化

在每层金字塔层中，密集偏移量$s_t^l$通过使用卷积块将残差偏移量添加到上一级别的偏移量$s_t^{l+1}$中进行迭代优化。 在偏移量预测网络中使用7×7的内核，以确保在大感受野下进行密集计算，计算如下：$$\begin{array}{rl}l& =L,\dots ,0\\ s_t^l& ={\mathcal{C}}_{\mathcal{S}}^l\left(f_t^l,v_t^l,U_{\uparrow }\left(s_t^{l+1}\right)\right)+U_{\uparrow }\left(s_t^{l+1}\right),s_t^L={\mathcal{C}}_{\mathcal{S}}^L\left(f_t^L\right)\end{array}$$

隐藏状态融合

最终，顶层偏移量$s_t^0$用于在t时刻融合显著的隐藏状态特征，另一个可变性注意块计算出$v_t^h$，如下所示：$$v_t^h\left(Q_t^0,K_{t-1}^h,V_{t-1}^h\right)=\mathrm{softmax}\left(\frac{Q_t^0{K}_{t-1}^{h^T}}{\sqrt{d}}\right)V_{t-1}^h$$此外在运行时的所有阶段对内部张量进行分组采样，根据采样的键/值对k=4的数量选择组的数量。

实验

消融实验

不同组件和通道数量的消融实验：

最先进的双向方法的一个核心特征是能够在整个视频中离线融合信息。这自然包括反向时间顺序的聚合。由于本文研究了前向/后向评估之间的差异。令人惊讶的是，反向时间顺序聚合显著提高了性能。作者将这种增益归因于摄像机的前向运动在视频中更为普遍。如果对象朝着相机移动，或者反之亦然，则它们首先以高分辨率出现，从而简化了这些对象的超分辨率。因此，有机会反向处理视频可能会提高VSR的性能，从而使非因果方法比在线算法具有更多优势。

定量评估

在REDS4、UDM10、Viemo-90K上的定量评估：

定性评估

在REDS上的定性评估：