详解Transformer
文章目录
- 参考文章
- 前言
-
- 采用attention机制的原因
-
- 1 RNN无法并行处理
- 2 CNN需要堆叠层数过深
- 3 transformer闪亮登场
- Transformer详解
-
- 1、 整体架构图
- 1.1 从整体上来看Transformer
- 1.2 输入编码
- 1.3 Self-Attention
-
- 这里给一个整体计算图
- 1.3.1 Self-Attention at a High Level(从宏观上看Self-Attention)
- 1.3.2.Self-Attention的实现细节
-
- First Step
- Second Step
- Third and Forth Steps
- Fifth Step
- Sixth Step
- 1.3.3 矩阵方式计算Self-Attention
-
- First Step
- Finally
- 1.3.4 Q、K、V的解释
- 1.5 Multi-Head Attention
- 1.6 位置编码
- 1.7 The Residuals(残差)
- 1.8 Decoder
- 1.9 最后的Linear和Softmax layer
- 1.10 训练过程的概况
- 1.11 损失函数
- 3 总结
-
- 优点
- 缺点
- 附录
-
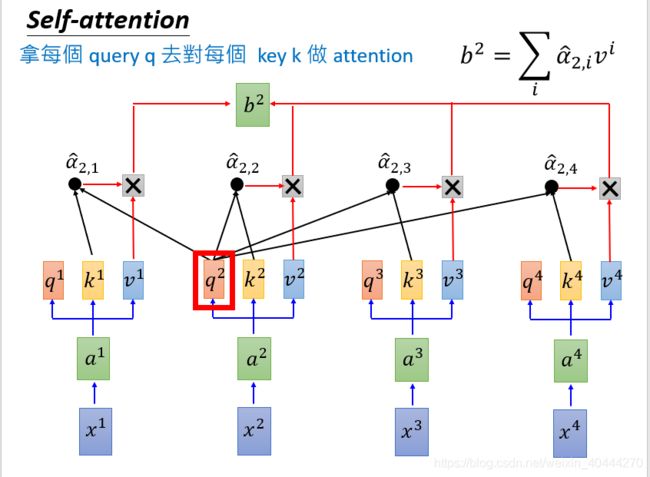
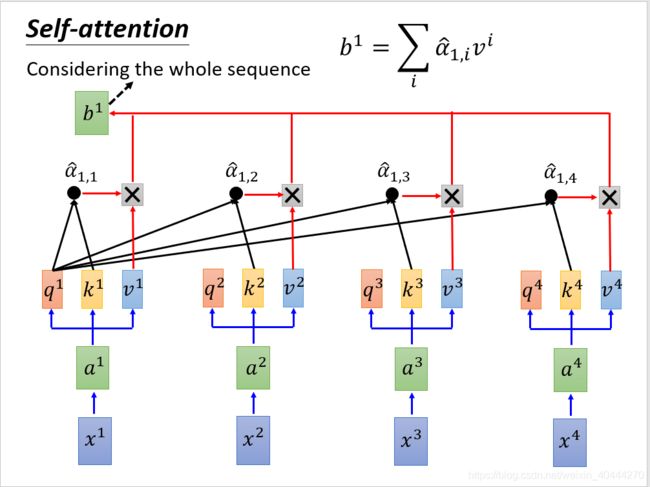
- 李宏毅机器学习self-attention计算过程
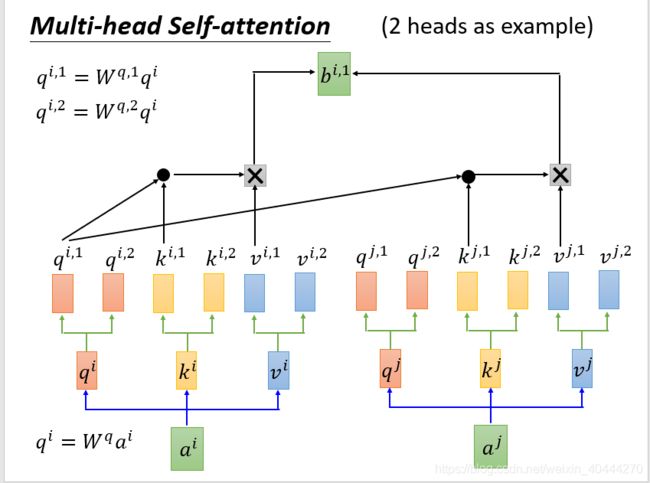
- multi-head attention
参考文章
详解Transformer (Attention Is All You Need)
The Illustrated Transformer
李宏毅机器学习
Attention all you need
《神经网络与深度学习》–邱锡鹏
前言
Transformer中完全抛弃了传统的CNN和RNN,整个网络结果完全是由Attention机制组成。
更准确地讲,Transformer由且仅由self-Attention和Feed Forward Neural Netword组成。
一个基于Transformer的可训练的神经网络通过堆叠Transformer的形式进行搭建,作者的实验是通过搭建编码器和解码器各6层,总共12层的Encoder-Decoder,并在机器翻译任务中取得了BLEU值的新高。
采用attention机制的原因
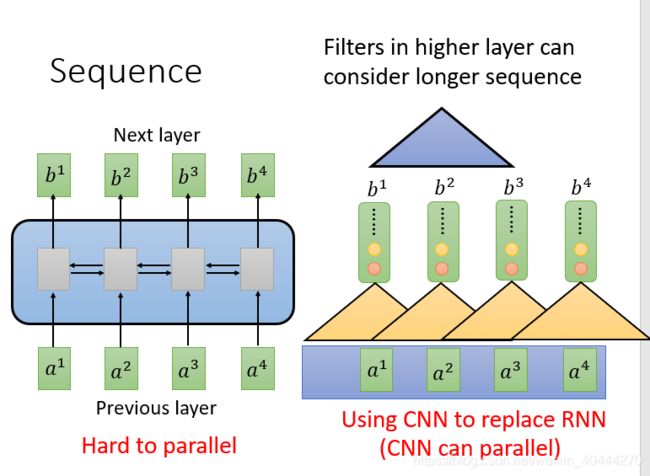
1 RNN无法并行处理
RNN(或者LSTM、GRU等)的计算限制为是串行计算(顺序计算),也就是说RNN相关算法只能从左到右依次进行计算或者从右向左进行计算。
这导致的问题
- 时刻
t的计算依赖t-1时刻的计算结果,模型只能顺序计算(sequential computation),这限制了模型的并行处理能力; - 顺序计算的过程中信息会丢失,尽管
LSTM等门机制的结构一定程度上缓解了长期依赖的问题,但是对应特别长的依赖现象,LSTM依旧无能为力
2 CNN需要堆叠层数过深
使用下图右边的CNN架构可以进行并行计算,但是input的所有序列每个CNN只能覆盖一部分,若想找到任意输入序列之间的关系需要建立更深的网络层数,加大了计算开销
3 transformer闪亮登场
transformer的提出解决了上述的两个问题,首先其使用了attention机制,将序列中的任意两个位置之间的距离缩小为一个常量;
其次它不是类似RNN的顺序结构,因此具有良好的并行性,符合GPU框架,可用GPU进行加速
Transformer详解
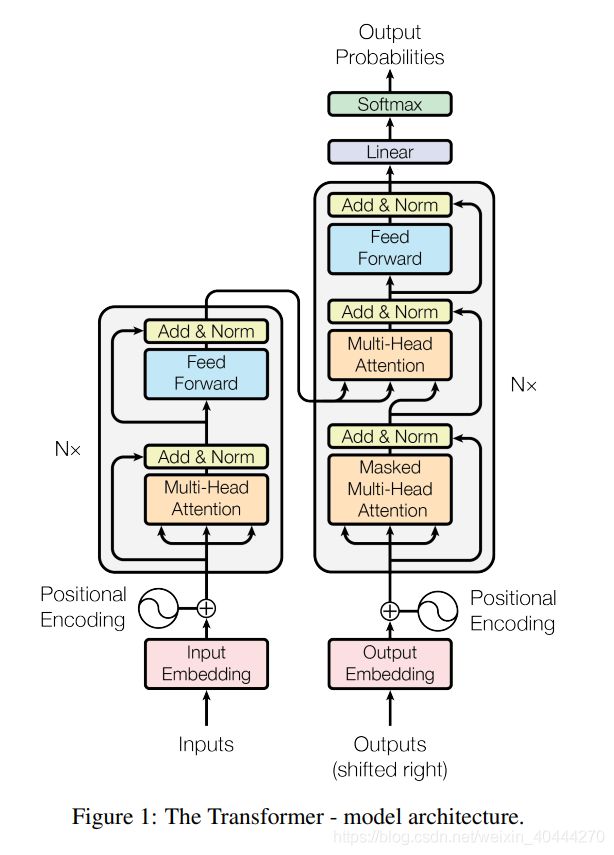
1、 整体架构图
1.1 从整体上来看Transformer
论文中的验证Transformer的实验室是基于机器翻译任务的,下面以机器翻译为例子详细剖析Transformer的结构,在机器翻译中,Transformer可概括为下图

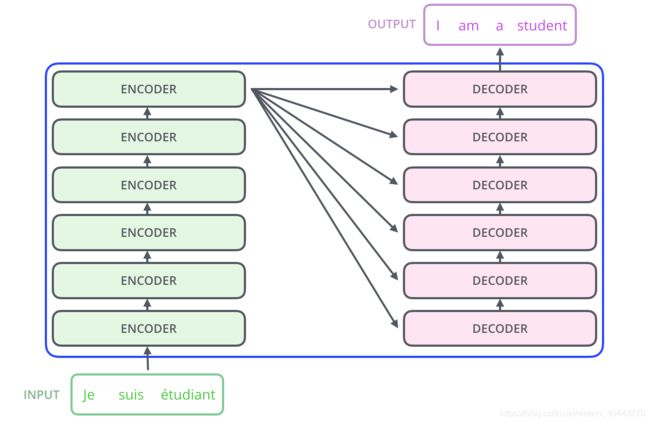
Transformer的本质是一个Encoder-Decoder的结构,上图中间的结构如下图所示

论文中设计的Encoder是由6个encoder block组成,同样Decoder是6个decoder block组成
与所有的生成模型相同的是,编码器(Encoder)的输出作为解码器(Decoder)的输入,如下图所示
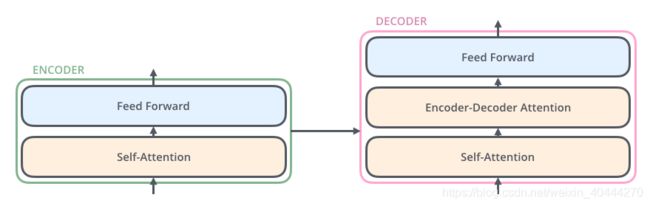
分析每个encoder的详细结构:
在Transformer的encoder中,数据首先会经过self-Attention模块,得到一个加权之后的特征向量 Z Z Z,这个 Z Z Z就是论文公式中的 A t t e n t i o n ( Q , K , V ) Attention(Q,K,V) Attention(Q,K,V):
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V (1) Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\tag{1} Attention(Q,K,V)=softmax(dkQKT)V(1)
该公式的实际含义将在后面进行解释
得到 Z Z Z之后,它会被送到encoder的下一个模块,即Feed Forward Neural Network。
这个全连接层有两层,第一层的激活函数是ReLU,第二层是一个线性激活函数,表示为:
F N N ( Z ) = m a x ( 0 , Z W 1 + b 1 ) W 2 + b 2 (2) FNN(Z) = max(0,ZW_1+b_1)W_2 +b_2\tag{2} FNN(Z)=max(0,ZW1+b1)W2+b2(2)
Encoder的结构图如下所示
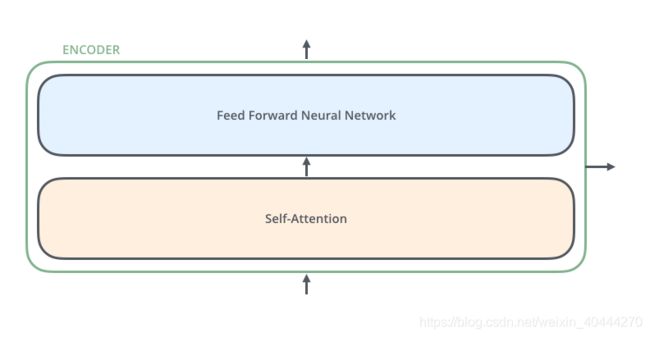
Decoder的结构图如下图所示
其与Encoder的不同之处在于Decoder多了一个Encoder-Decoder Attention,两个Attention分别用于计算输入和输出的权值:
Self-Attention:当前翻译和已经翻译的前文之间的关系Encoder-Decoder Attention:当前翻译和编码的特征向量之间的关系
1.2 输入编码
上一节讲述Transformer的主要框架,下面我们将介绍它的输入数据。
如下图所示,首先通过Word2Vec等词嵌入方法将输入语料转化为特征向量,论文中使用的词嵌入的维度为 d m o d e l = 512 d_{model}=512 dmodel=512
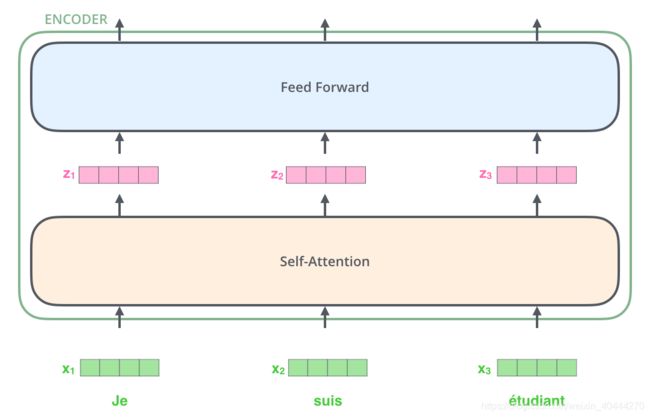
下图中,在Self-Attention层中各个x都存在着相关性,但是在Feed Forward层中却失去了相关性(dependencies)。
这样就使得Feed Forward可以并行处理
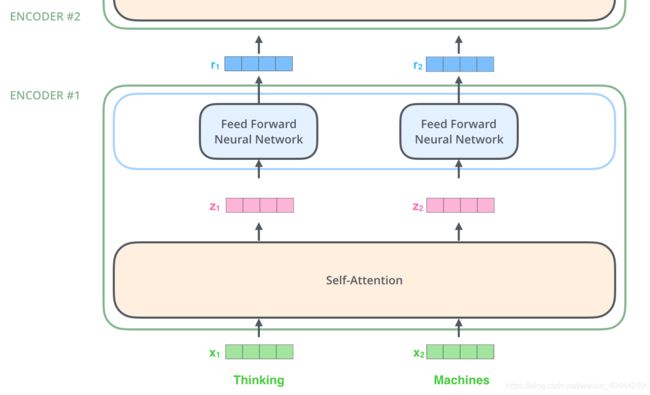
下图就是一个Encoder的处理过程,首先将输入序列转为vector,然后vector经过Self-Attention,再经过Feed Forward,然后将结果输出到下一个Encoder
1.3 Self-Attention
self attention的计算过程可以参考最后附录。
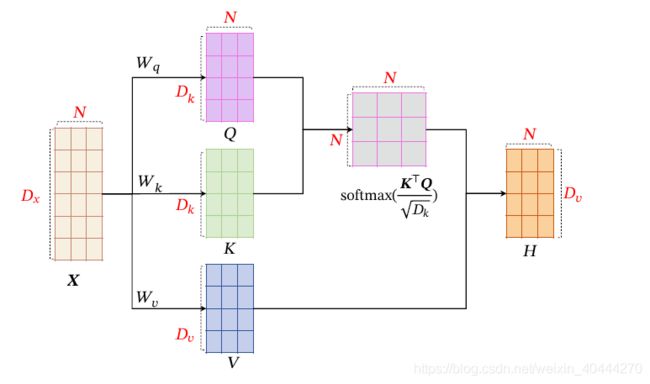
这里给一个整体计算图
1.3.1 Self-Attention at a High Level(从宏观上看Self-Attention)
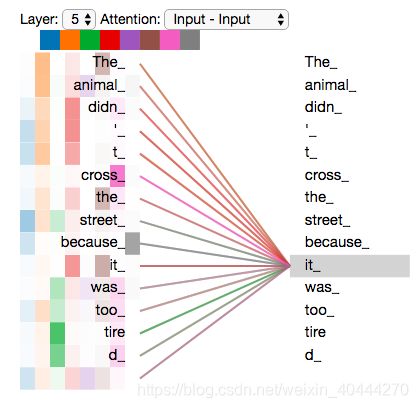
Self-Attention是Transformer的核心内容,其为输入变量的每个单词学习一个权重,例如下面的示例,找出it所代指的内容
The animal didn't cross the street because it was too tired
通过加权之后得到类似下图的加权表示
访问此链接可查看此图实现的代码
1.3.2.Self-Attention的实现细节
Self-Attention计算的详细细节
First Step
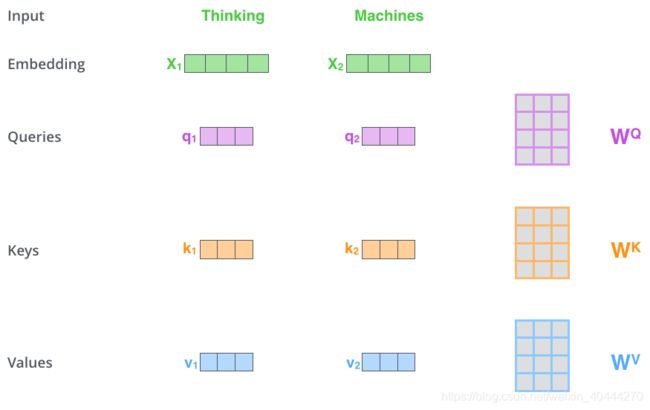
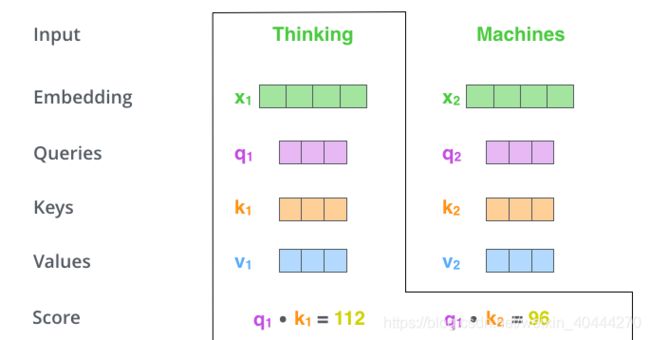
对于每个input vectors(这里是指词嵌入)都有 3 3 3个不同的vector,分别是 Q Q Q(Query向量)、 K K K(Key向量)、 V V V(Value向量)。
note:这三个vector的维度要小于word embedding时获得的向量维数,此处长度均为 64 64 64。
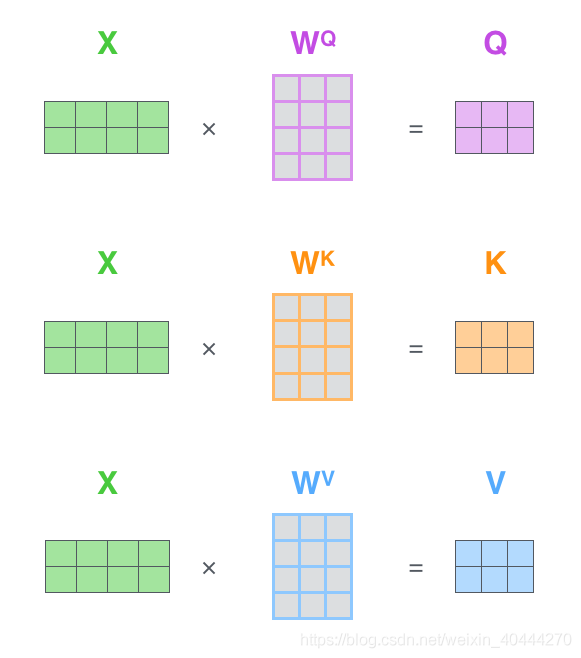
它们是通过 3 3 3个不同的权值矩阵由嵌入向量 X X X乘以三个不同的权值矩阵 W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV(在训练模型中训练而得)得到,这三个矩阵的shape也相同,均为 512 × 64 512 \times 64 512×64
q 、 k 、 v q、k、v q、k、v的计算过程
- q 1 = X 1 × W Q q_1 = X_1 \times W^Q q1=X1×WQ
- k 1 = X 1 × W K k_1 = X_1 \times W^K k1=X1×WK
- v 1 = X 1 × W V v_1 = X_1 \times W^V v1=X1×WV
Query,Key,Value是什么意思?它们在Attention的计算中扮演着什么角色?
在后面进行解释
Second Step
主要是计算score
对“Thinking Matchines”这句话,以计算第一个单词"Thinking"为例。
计算"Thinking Matchines"中每个单词对于"Thinking"的score,这个score表示对于“Thinking”这个词(序列中某个确定位置的值),"Thinking Matchines"(input sequences)中的其他单词对其的关注程度。
第一个score
S c o r e : q 1 ⋅ k 1 Score:q_1 \cdot k_1 Score:q1⋅k1
第二个score
S c o r e : q 1 ⋅ k 2 Score:q_1 \cdot k_2 Score:q1⋅k2
Third and Forth Steps
将score除以 k d \sqrt{k_{d}} kd,这是为了让让梯度更加稳定,也可以除以其他值,这里使用的是默认方式。
s c o r e = s c o r e k d score = \frac{score}{\sqrt{k_d}} score=kdscore
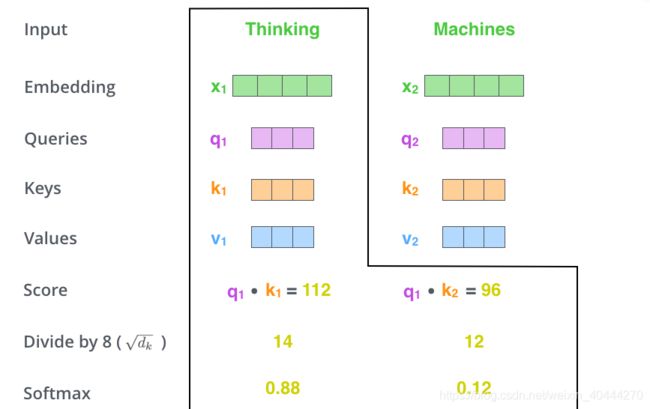
再将得到的score经过softmax层
s c o r e = s o f t m a x ( s c o r e ) score = softmax(score) score=softmax(score)
经过softmax之后的各个score,表示在这个位置("Thinking"),收到其他各个词的关注程度。
当然这个词自己对自己关注的程度最高,但大部分时候总是有助于关注该词的相关的词。
Fifth Step
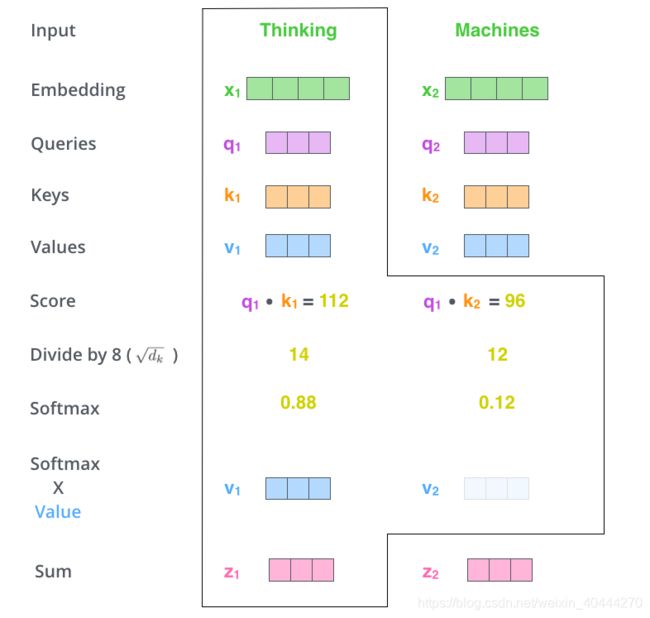
将softmax之后的score与v进行相乘,这样可以保留相关词的value,削弱不相关词的value
v 1 = s o f t m a x ( s c o r e ) × v 1 v_1 = softmax(score) \times v_1 v1=softmax(score)×v1
Sixth Step
将上一步得到的vector进行求和,这就产生第一个单词("Thinking"),在Self-Attention中的值
z : z 1 = ∑ i = 1 n v i = v 1 + v 2 z:z_1 = \sum_{i=1}^{n} v_i = v_1 + v_2 z:z1=i=1∑nvi=v1+v2
1.3.3 矩阵方式计算Self-Attention
First Step
收件计算出Query、Key、Value这三个matrix
Finally
1.3.4 Q、K、V的解释
Query,Key,Value的概念取自于信息检索系统,
举个简单的搜索的例子来说。当你在某电商平台搜索某件商品(年轻女士冬季穿的红色薄款羽绒服)时,你在搜索引擎上输入的内容便是Query,然后搜索引擎根据Query为你匹配Key(例如商品的种类,颜色,描述等),然后根据Query和Key的相似度得到匹配的内容(Value)。
self-attention中的 Q , K , V Q,K,V Q,K,V也是起着类似的作用,在矩阵计算中,点积是计算两个矩阵相似度的方法之一,因此式1中使用了 Q K T QK^T QKT 进行相似度的计算。接着便是根据相似度进行输出的匹配,这里使用了加权匹配的方式,而权值就是query与key的相似度。
1.5 Multi-Head Attention
论文中在Self-Attention层中添加"multi-headed" attention,这可以在两个方面提高attention层的表现
1.multi-headed attention机制扩展了模型关注(focus on)不同位置的能力。在上面的例子中, z 1 z_1 z1只包含了其他编码的很少信息,实际上仅由它自己决定。在某些情况下,比如翻译 “The animal didn’t cross the street because it was too tired”时,我们想知道单词"it"指的是什么。
2.multi-headed attention机制赋予attention多种子表达方式。像下面的例子所示,在此情况下有多组query/key/value-matrix,而非仅仅一组(论文中使用8-heads)。每一组都是随机初始化,经过训练之后,输入向量可以被映射到不同的子表达空间中。
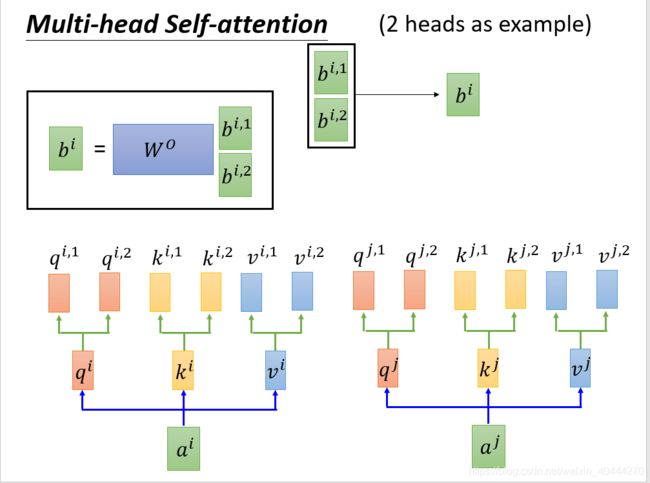
下图展示两个head的情况
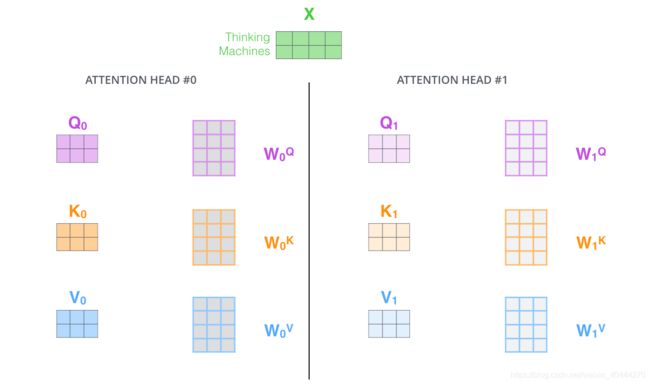
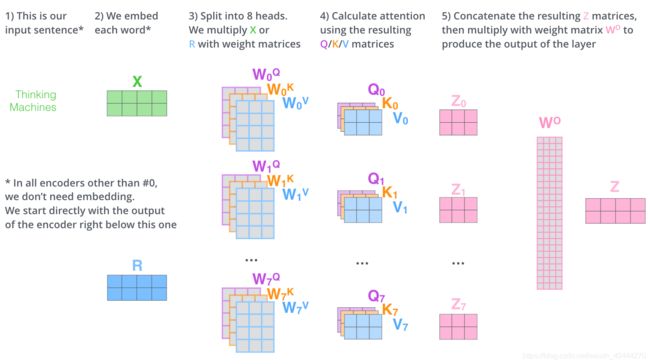
如果我们计算multi-headed self-attention的,分别有八组不同的Q/K/V matrix,我们得到八个不同的矩阵。
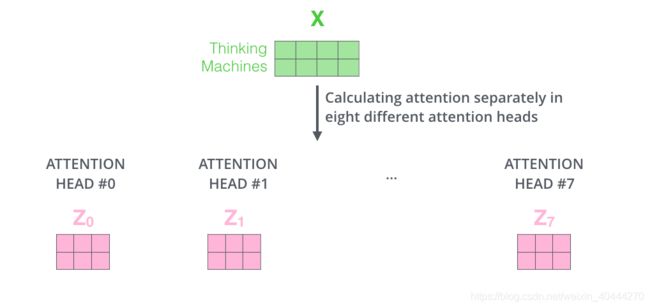
前向网络并不能接收八个矩阵,而是希望输入是一个矩阵,所以要有种方式处理下八个矩阵合并成一个矩阵。
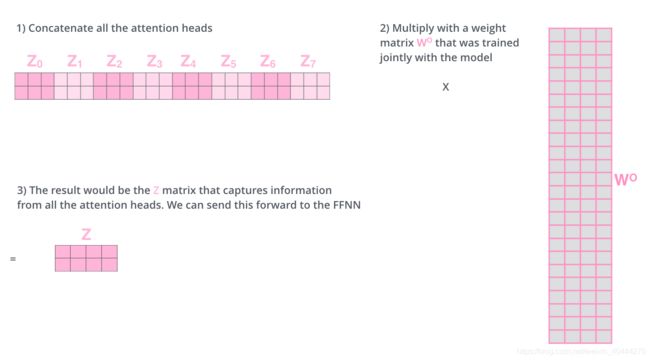
上述就是multi-headed self-attention
将它们放到一个图上可视化如下。
加入了multi-head机制,对前面的例子重新看一下

编码"it"时,一个attention head集中于"the animal",另一个head集中于“tired”,某种意义上讲,模型对“it”的表达合成了的“animal”和“tired”两者
1.6 位置编码
截至目前为止,我们所介绍的Transformer模型并没有捕捉顺序序列的能力,也就是说其并不在意句子的顺序,无论顺序如何产生的结果都会类似。这就相当于Transformer是一个功能更强大的词袋模型而已。
为了解决这个问题,论文中在编码词向量时引入了位置编码(Position Embedding)的特征,具体来说,位置编码会在词向量中加入了单词的位置信息,这样Transformer就能区分不同位置的单词了。
如何编码位置信息,常见模式:a.根据数据学习;b.自己设计编码规则
作者采用第二种方式,这个位置编码是一个长度为 d m o d e l d_{model} dmodel的特征向量,这样便于和词向量进行单位加操作,如图16
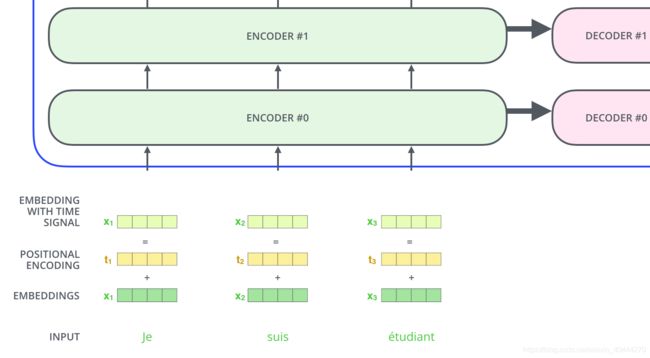
假设embedding的维数为 4 4 4,那么实际的positional encodings就会类似下图
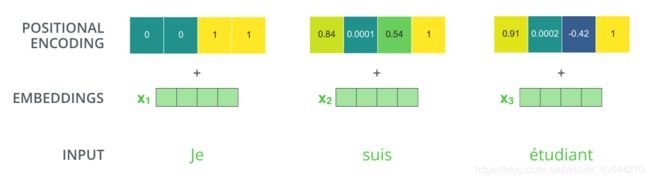
论文给出的位置编码公式如下:
P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i d m o d e l ) PE(pos,2i) = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) PE(pos,2i)=sin(10000dmodel2ipos)
P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i d m o d e l ) PE(pos,2i+1) = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) PE(pos,2i+1)=cos(10000dmodel2ipos)
- p o s pos pos表示单词在句子的位置,若是句子长度为 L L L,则 p o s = { 0 , 1 , . . . , L − 1 } pos=\lbrace 0,1,...,L-1 \rbrace pos={0,1,...,L−1}
- i i i表示向量的某一维度,假设 d m o d e l = 512 d_{model} =512 dmodel=512,那么 i = { 1 , 2 , . . . . , } i= \lbrace 1,2,...., \rbrace i={1,2,....,}
根据上式即可为每个位置上的token生成 d m o d e l d_{model} dmodel维的位置向量
作者这么设计的原因是考虑到在NLP任务中,除了单词的绝对位置,单词的相对位置也非常重要。
根据公式
s i n ( α + β ) = s i n α c o s β + c o s α s i n β sin(\alpha + \beta) = sin\alpha cos\beta + cos\alpha sin\beta sin(α+β)=sinαcosβ+cosαsinβ
c o s ( α + β ) = c o s α c o s β − s i n α s i n β cos(\alpha + \beta) = cos\alpha cos\beta - sin\alpha sin \beta cos(α+β)=cosαcosβ−sinαsinβ
这表明位置 k + p k+p k+p 的位置向量可以表示为位置 k k k的特征向量的线性变化,这为模型捕捉单词之间的相对位置关系提供了非常大的便利。
Google开源算法中找到get_timing_signal_1d()
1.7 The Residuals(残差)
残差网络的解析近几天就会编写
Encoder中值得提出注意的一个细节是,在每个子层中(Self-Attention, Feed Forward),都有残差连接,并且紧跟着layer-normalization。
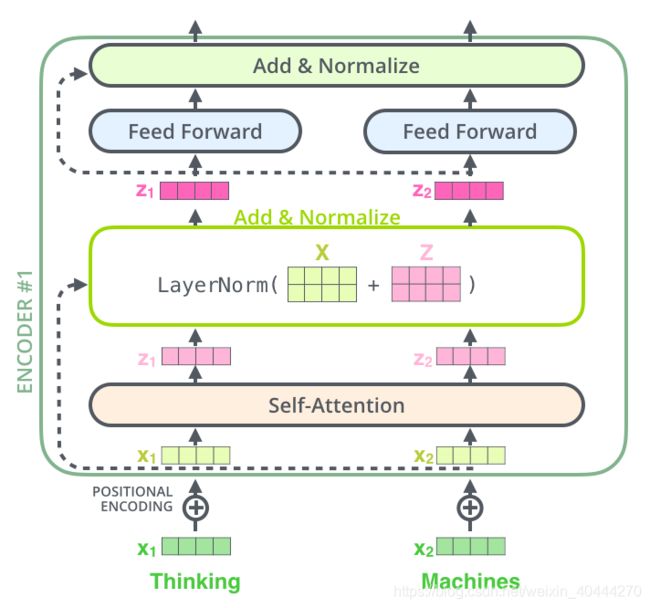
在Decoder中也是如此,假设两层Encoder+两层Decoder组成Transformer,其结构如下:
1.8 Decoder
我们已经明白Encoder的大部分概念,现在开始了解Decoder的工作流程。
Encoder接受input sequence转换后的vector,然后最后的Encoder将其转换为K、V这两个被每个Decoder的"encoder-decoder atttention"层来使用,帮助Decoder集中于输入序列的合适位置。
下面的步骤一直重复直到一个特殊符号出现表示解码器完成了翻译输出。
每一步的输出被下一个解码器作为输入。
正如编码器的输入所做的处理,对解码器的输入增加位置向量。
encoder与decoder在Self-Attention层中会有些许不同。Decoder比Encoder多了一个encoder-decoder attention。
在encoder-decoder attention中, Q Q Q 来自于与Decoder的上一个输出, K K K和 V V V则来自于与Encoder的输出。其计算方式完全和图10的过程相同。
由于在机器翻译中,解码过程是一个顺序操作的过程,也就是当解码第 k k k 个特征向量时,我们只能看到第 k − 1 k-1 k−1及其之前的解码结果,论文中把这种情况下的multi-head attention叫做masked multi-head attention。
1.9 最后的Linear和Softmax layer
最终使用Linear和Softmax作为输出
Linear Layer是一个简单的全连接层,将Decoder的最后输出映射到一个logits向量上。
假设模型有1w个单词(输出的词表)从训练集中学习获得。那么logits向量就有1w维,每个值表示某个词的可能倾向值。
softmax则将logits的分数转为概率值(范围[0,1],和为1),最高值对应的维上是这一步的输出单词。
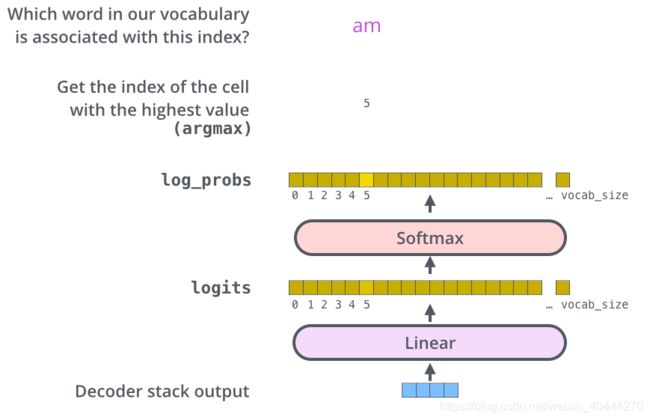
1.10 训练过程的概况
在训练时,模型将经历上述步骤。
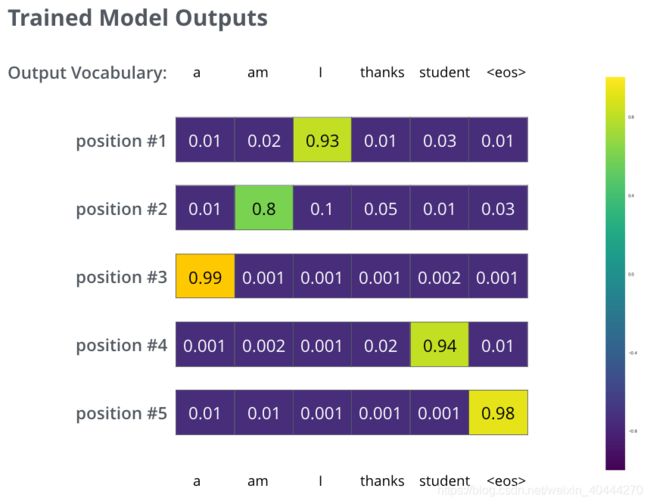
假设我们的输出词只有六个(“a”, “am”, “i”, “thanks”, “student”, and “” (short for ‘end of sentence’))。这个输出词典在训练之前的预处理阶段创建。
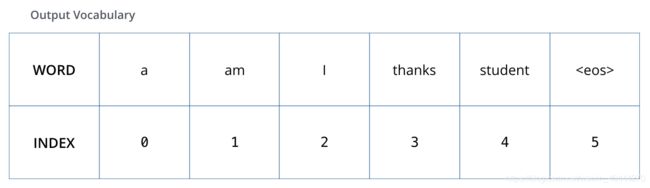
定义词表之后,我们可以使用相同width的vector来表示词表上的每个单词。
例如使用one-hot编码。am使用下图的表示方式。

根据此方式来讨论以下损失函数–在训练过程中用于优化的指标
1.11 损失函数
以一个简单的示例进行讲解,将merci(法语)翻译为thanks。
这意味着输出的概率分布指向单词"thanks",但是由于模型未训练是随机初始化,输出可能并不准确。
根据输出值与实际值进行比较,然后根据后向传播算法进行调参,使得结果更加准确。
如何对比两个概率分布呢?简单采用 cross-entropy或者Kullback-Leibler divergence中的一种。
此次举例非常简单,真实情况下应当以一个句子作为输入。比如,输入是“je suis étudiant”,期望输出是“i am a student”。在这个例子下,我们期望模型输出连续的概率分布满足如下条件:
- 每个概率分布都与词表同维度。
- 第一个概率分布对“i”具有最高的预测概率值。
- 第二个概率分布对“am”具有最高的预测概率值。
- 一直到第五个输出指向""标记。
3 总结
优点
-
虽然Transformer最终也没有逃脱传统学习的套路,
Transformer也只是一个全连接(或者是一维卷积)加Attention的结合体。但是其设计已经足够有创新,因为其抛弃了在NLP中最根本的RNN或者CNN并且取得了非常不错的效果,算法的设计非常精彩,值得每个深度学习的相关人员仔细研究和品位。 -
Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是 1 1 1,这对解决NLP中棘手的长期依赖问题是非常有效的。 -
Transformer不仅仅可以应用在NLP的机器翻译领域,甚至可以不局限于NLP领域,是非常有科研潜力的一个方向。 -
算法的并行性非常好,符合目前的硬件(主要指GPU)环境。
缺点
-
粗暴的抛弃
RNN和CNN虽然非常炫技,但是它也使模型丧失了捕捉局部特征的能力,RNN + CNN + Transformer的结合可能会带来更好的效果。 -
Transformer失去的位置信息其实在NLP中非常重要,而论文中在特征向量中加入Position Embedding也只是一个权宜之计,并没有改变Transformer结构上的固有缺陷。
附录
权当一个辅助参考