卷积神经网络学习小结——1基本概念与单层神经网络实现
疫情严重,待在家中无事,回想研究生生活已经转眼过去半年,然而买的李航的《统计学习方法》这本书还没有看,想到同门关于CNN的文章都快要发了,所以学习了一点关于卷积神经网络(Convolution net work)方面的东西,希望对在日后的激光雷达工作中有所用,在此对已经学习完的东西进行一个简要的小结:
学习参考资料:
- 视频:
- 吴恩达 Deep Learning-Convolutional Neural Networks(为主)
- 莫烦pytorch教学
- 书籍:
- pytorch-handbook
- 《动手学习神经网络(Pytorch实现)》
基本概念目录:
- 1 基本概念
- 1.1单层神经网络
- 线性回归(连续值,回归)
- softmax回归(离散值,分类)
- 1.1单层神经网络
1.1单层神经网络
1.1.1线性回归
Y ~ = w 1 ∗ x 1 + w 2 ∗ x 2 + b \tilde{Y}=w_1*x_1+w_2*x_2+b Y~=w1∗x1+w2∗x2+b
其中和 w 1 w_1 w1 和 w 2 w_2 w2 是权重(weight), b b b 是偏差(bias),且均为标量。它们是线性回归模型的参数(parameter),就是 y = a x + b y=ax+b y=ax+b中的 a a a和 b b b。模型输出 y ~ \tilde y y~ 是线性回归对真实价格 yy 的预测或估计。权重和偏差往往都会存在误差,导致预测值和真值之间往往存在差距。
接下来我们需要通过数据来寻找特定的模型参数值,使模型在数据上的误差尽可能小。这个过程叫作模型训练(model training)。
模型训练往往分为三步:
1 获取数据
样本(sample):群体中的个体
标签(label):想要预测的值 ( y 1 ) i (y_1)^i (y1)i
特征(feature):个体用于预测标签的多种特性值 ( x 1 ) i (x_1)^i (x1)i、 ( x 2 ) i (x_2)^i (x2)i
训练集(training set):样本+标签+特征 的集合
2 损失函数
损失函数(loss function):衡量估计预测模型和真实值之间的误差。常我们会选取一个非负数作为误差,且数值越小表示误差越小。一个常用的选择是平方函数。
在模型训练中,我们希望找出一组模型参数,记为 w 1 ∗ w_1^∗ w1∗, w 2 ∗ w_2^∗ w2∗, b ∗ b^∗ b∗
w 1 ∗ , w 2 ∗ , b ∗ = a r g . l o s s ( m i n ( w 1 , w 2 , b ) ) w_1^*,w_2^*,b^* = arg .loss(min(w_1,w_2,b)) w1∗,w2∗,b∗=arg.loss(min(w1,w2,b))
3 优化算法
数值解(numerical solution):深度学习模型并没有解析解(误差最小化问题的解可以直接用公式表达出来),只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。
小批量随机梯度下降(mini-batch stochastic gradient descent):
初始值→随机均匀小批量(mini-batch)→平均损失梯度→迭代减少量
- 超参数(hyperparameter)是人为设定的,并不是通过模型训练学出的,因此叫作超参数。
- 优化算法里面代表每个小批量中的样本个数(批量大小,batch size),学习率(learning rate)就是超参数。
4线性回归的表示方法
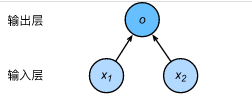
如图所示,输入分别为 x 1 x_1 x1和 x 2 x_2 x2,因此输入层的输入个数为2。
输入个数也叫特征数或特征向量维度。图中网络的输出为 o o o,输出层的输出个数为1。
需要注意的是,我们直接将图3.1中神经网络的输出 oo 作为线性回归的输出,即 y ~ = o \tilde{y}=o y~=o。由于输入层并不涉及计算,按照惯例,图中所示的神经网络的层数为1。所以,线性回归是一个单层神经网络。
输出层中负责计算 o o o 的单元又叫神经元。输出层中的神经元和输入层中各个输入完全连接。因此,这里的输出层又叫全连接层(fully-connected layer)或稠密层(dense layer)。
5 线性回归代码实现
#代码来源上述两个文件中
#单层神经网络构建——线性回归(预测)
import torch
import numpy as np
import torch.utils.data as Data #torch 读取数据的模块
import torch.nn.modules as nn #torch 构建模型的模块
from torch.nn import init #torch 初始化参数的模块
import torch.optim as optim #torch 优化算法
import matplotlib.pyplot as plt
# 1.生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
print(features)
# 生成数据的两个特征,两列(0,1)正态分布的1000个数 !!数据格式选择是浮点数
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# 生成标签,y=w1*x1+w2*x2+b,一列
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
# 在标签中加入误差,1000个数(0,0.01)的正态分布
# 2.读取数据
batch_size = 10
# 小批量的值
dataset = Data.TensorDataset(features, labels)
# 将训练数据的特征和标签组合
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
# 随机读取小批量 !!shuffle = True 是随机的意思
# 3.定义模型
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__() #继承nn.Module的性质,构建层次
self.linear = nn.Linear(2,1,bias=True) #线性层
#定义前向传播
def forward(self,x):
y = self.linear(x)
return y
net = Net()
# 使用print可以打印出网络的结构,三个名字参数(2个W一个B)
for name,parameters in net.named_parameters():
print(name,':',parameters.size())
# 4.模型参数初始化
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias,val=0)
# 5.定义损失函数
loss = nn.MSELoss()
# 6.定义优化算法
optimizer = optim.SGD(net.parameters(), lr=0.03) # 全部参数学习率为0.03
# 7.训练模型
num_epochs = 20
lossval = np.zeros(shape = (1,num_epochs+1))
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # !!梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
lossval[0][epoch-1] = l.item()
print('epoch %d, loss: %f' % (epoch, l.item()))
# 绘制loss曲线
# plt.plot(lossval[0], 'r', label='loss')
# plt.legend(loc='best')
# plt.show
# 8.查看参数
# dense = net.linear()
print(true_w, net.linear.weight)
print(true_b, net.linear.bias)
# 9.模型进行预测
test_x = np.random.rand(50,2)
real_y = 2*test_x[:,0] -3.4*test_x[:,1] +4.2
test_x = torch.tensor(test_x,dtype = torch.float)
pre_y = net(test_x)
# 10.绘制图像
plt.plot(pre_y.data.numpy(), 'r', label='prediction')
plt.plot(real_y, 'b', label='real')
plt.legend(loc='best')
plt.show()
1.1.2softmax回归
softmax回归与线性回归的区别:
- softmax回归的输出单元从一个变成了多个
- softmax运算使输出更适合离散值的预测和训练
1 Softmax模型
softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于,softmax回归的输出值个数等于标签里的类别数。
假设一个简单的的图像分类问题,其输入图像的高和宽均为2像素,且色彩为灰度(221)。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4。。假设训练数据集中图像的真实标签为狗、猫或鸡(假设可以用4像素表示出这3种动物),这些标签分别对应离散值 y 1 , y 2 , y 3 y_1,y_2,y_3 y1,y2,y3。
o 1 = w 11 ∗ x 1 + w 12 ∗ x 2 + w 13 ∗ x 3 + w 14 ∗ x 4 + b 1 o_1= w_{11}*x_1+w_{12}*x_2+w_{13}*x_3+w_{14}*x_4+b_1 o1=w11∗x1+w12∗x2+w13∗x3+w14∗x4+b1
o 2 = w 21 ∗ x 1 + w 22 ∗ x 2 + w 23 ∗ x 3 + w 24 ∗ x 4 + b 2 o_2= w_{21}*x_1+w_{22}*x_2+w_{23}*x_3+w_{24}*x_4+b_2 o2=w21∗x1+w22∗x2+w23∗x3+w24∗x4+b2
o 3 = w 31 ∗ x 1 + w 32 ∗ x 2 + w 33 ∗ x 3 + w 34 ∗ x 4 + b 2 o_3= w_{31}*x_1+w_{32}*x_2+w_{33}*x_3+w_{34}*x_4+b_2 o3=w31∗x1+w32∗x2+w33∗x3+w34∗x4+b2

分类问题是输出值如何转化为离散值的问题,简单的办法是将输出值 o i o_i oi,当作预测类别是 i i i的置信度,并将值最大的输出所对应的类作为预测输出,取各类别最高值作为类别。但是最高值往往相对的情况,所以遇到这种情况会将下式将输出值变换成值为正且和为1的概率分布(即softmax operator),然后最转为预测类别输出。
softmax回归对样本ii分类的矢量计算表达式为
o ( i ) = x ( i ) W + b o^{(i)}=x^{(i)}W+b o(i)=x(i)W+b
p ( y ( i ) ) = s o f t m a x ( o ( i ) ) p(y^{(i)})=softmax(o^{(i)}) p(y(i))=softmax(o(i))
2 交叉熵损失函数
最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
3 模型预测及评价
- 通常,我们把预测概率最大的类别作为输出类别
- 使用准确率(accuracy)来评价模型的表现。它等于正确预测数量与总预测数量之比。
4 代码实现(这段代码仅供参考,详细会在卷积神经网络实现中出现)
#单层神经网络构建——softMax(分类)
#该段代码存在问题
import torch
import numpy as np
import torch.utils.data as Data #torch 读取数据的模块
import torch.nn.modules as nn #torch 构建模型的模块
from torch.nn import init #torch 初始化参数的模块
import torch.optim as optim #torch 优化算法
import matplotlib.pyplot as plt
import torchvision
import torchvision.transforms as transforms
import sys
# 1.读取数据
mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
batch_size = 256
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
# 2.定义初始化模型
num_inputs = 784
num_outputs = 10
class LinearNet(nn.Module):
def __init__(self, num_inputs, num_outputs):
super(LinearNet, self).__init__()
self.linear = nn.Linear(num_inputs, num_outputs)
def forward(self, x): # x shape: (batch, 1, 28, 28)
y = self.linear(x.view(x.shape[0], -1))
return y
net = LinearNet(num_inputs, num_outputs)
# 3.定义初始参数
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)
# 4.交叉熵值和softmax分类 () LogSoftmax
loss = nn.CrossEntropyLoss()
# 5.定义优化器
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
# 6.训练模型
num_epochs, lr = 5, 0.1
# 7.定义精确度
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
# 8.训练
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
小结
1.线性回归和softmax都是单层全连接神经网络,一个是连续值用于回归,一个是离散值用于分类
2.神经网络的基本步骤:获取并读取数据、定义模型和损失函数并使用优化算法训练模型。