Image-to-image translation with Conditional Adversarial Networks——基于cGAN的图像转换
文章目录
-
- 论文背景介绍 Background Introduction
- 相关工作 Related Work
-
- 图像模型的结构化损失 —— Structured losses for image modeling
- 条件对抗生成网络 —— Conditional GANs
- 方法 Method
-
- 指标 Objective
- 网络架构 Network Architecture
-
- 生成器 —— 跳跃式生成器(Generator with skip)
- 判别器 —— 马尔可夫判别器(Markovian Discriminator,PatchGAN)
- 优化和推断 Optimization & Inference
- 实验阶段 Experiment
-
- 评估方法 —— Evaluation Metrics
- 指标函数的分析 —— Analysis of Objective Function
- 生成器结构的分析 —— Analysis of Generator Architecture
- 从PixelGAN到PatchGAN再到ImageGAN
-
- 全卷积转换 Fully-convolutional translation
- 知觉验证 Perceptual Validation
- 图像分割 Semantic Segmentation
- 社区驱动调查 Community-driven Research
论文原文 —— pix2pix paper: Image-to-image with Conditional Adversarial Networks
论文背景介绍 Background Introduction
我们知道有很多的数字图像处理,计算机视觉都涉及到了一个问题,那就是:translating an input image into a corresponding output image,把一张输入的图片转换为一张对应的输出图片。
如下图所示,下图给出了若干从输入图像到输出图像的转换,涉及到了不同的算法,对应了不同类型的输入图片。例如,左下的手提包的转换,输入图像是一张边缘图像,最终输出的是一张几乎真实的皮质手提包图像;在它上面是一张灰度自然图像的输入,最终输出的是一张自然的彩色图像:
很显然这些都涉及到不同的算法(application-specific algorithm,具有特定应用的算法),但是归根到底,这都是一个相同的过程,那就是:map pixels to pixels,像素到像素的映射。
而现在我们希望:能否找到一种方法,可以广泛的适用于像这样的像素映射问题,用一种通用的方式代替这一系列大量的算法工作。
CNN的出现,为我们实现这个愿望迈出了非常重要的一步。CNN一个重要的部分是损失函数(losses function)——也就是一个指标(objective)的应用。通过学习来最小化这个损失函数,这个过程是自动的(automatic),但是还需要做一些工作:我们需要告诉CNN应该采用怎样的损失函数,也就是它应该对什么进行最小化。这是非常重要并且困难的工作,因为一个效果不佳的损失函数会得到非常不理想的结果。
像这样,假如我们告诉CNN,让它去最小化预测结果和真实结果之间的欧拉距离(Euclidean Distance),那么你可能会发现,输出结果将会只是一个经过模糊的结果(blurry result),因为CNN会对数据做一个平均来使得欧拉距离最小化。
那有没有可能,我们可以在一个更高的层面上告诉CNN我们希望它做什么,例如”请你尽可能的生成一张真实的图片“,然后能够自动学习得到一个损失函数来满足我们的要求呢?
那就是GAN(Generative Adversarial Network 生成对抗网络)了。同样的,GAN也是学习一个损失函数,但是不同的是,GAN生成非真实的图片,然后尽可能的去区分它是不是真实的。也就是说,GAN学习损失函数的方式是基于数据的,所以可以应用于大量具有不同的损失函数要求的任务。
这里,我们并不是直接使用GAN来进行图像转换,因为对于GAN来说,它的输入是一个随机的噪声向量,并期待能够生成更好的结果,但是,GAN可能并不知道我们希望它生成什么样的东西,因为输入是完全随机的!
显然,当我们希望GAN能够知道我们想做什么,例如”我们希望将一张边缘图像还原成一张真实的图像”,那么自然的,我们需要提供额外的条件,也就是额外的输入。
例如我们现在有这样一个工作:我们希望把将物体的边缘图像转换为真实的物体。这样的话,对于生成器来说,不仅是要输入一个随机变量,它肯定还需要这张边缘图像作为输入,因为这才是我们希望它完成的工作!
这就是cGAN(conditional Generative Adversarial Network,条件对抗生成网络)。如下图所示:

左边是一个生成器,右边是判别器。可以发现,不同于GAN的是,cGAN不仅判别器可以观察到输入的边缘图像,它的生成器同样可以观察到输入的边缘图。
我们的主要目标就是:希望能够展示出cGAN有能力对大多数的图像转换问题提供一个满意的结果。然后,我们希望找到这样的一种简单的框架,能够满足我们来得到这样一种好的结果,并对不同结构的选择分析它们的效果。
相关工作 Related Work
图像模型的结构化损失 —— Structured losses for image modeling
通常来说,图像转换都是一个像素到像素的过程。也就是说,对于输出空间来说,传统的方法都是非结构化的(unstructured),也就是说,我们并不会考虑像素和像素之间的关系。而cGAN则是学习一个结构化的损失(structured loss),对于结构化的损失,它会作用于输出的联合(?)(joint configuration of output),也就是说,它不是独立的对待每一个输出,对于cGAN来说,它可以对引起当前输出和目标输出不同的结构(structure)进行抑制(惩罚,penalize),而鼓励生成器去生成和目标相关的结构。
条件对抗生成网络 —— Conditional GANs
这并不是cGAN的第一次应用,在这篇论文之前,已经在其他方面做过许多相关的工作。而对于也有一些image-to-image相关的工作,都只是非条件生成对抗网络的运用(GAN unconditionally),采用的是别的方法施加相应的条件限制。
而这不仅仅是cGAN在图像转换上的应用,还有在结构的选择上,也与以往的工作有所不同:
- 生成器 —— ”U-net"-based结构
- 判别器 —— “PatchGAN”,Patch是图片的局部区域(局部视野)
方法 Method
指标 Objective
cGAN的指标如下:
(1) L c G A N ( G , D ) = E x , y [ l o g D ( x , y ) ] + E x , z [ l o g ( 1 − D ( x , G ( x , z ) ) ) ] \mathcal{L}_{cGAN}(G, D) = \mathbb{E}_{x, y}[logD(x, y)] + \mathbb{E}_{x, z}[log(1 - D(x, G(x, z)))] \tag{1} LcGAN(G,D)=Ex,y[logD(x,y)]+Ex,z[log(1−D(x,G(x,z)))](1)
其中,G就是生成器(G,Generator),它会尽可能的减少这个值,来生成更好的图片;而D是判别器(D,Discriminator),相反,它会尽可能的减少这个值,来提高自己的判别能力:
(2) G ∗ = arg min max L c G A N ( G , D ) G^{*} = \arg\min\max\mathcal{L}_{cGAN}(G,D) \tag{2} G∗=argminmaxLcGAN(G,D)(2)
而对于GAN(unconditionally)来说,它并不会观察输入 x x x:
(3) L G A N ( G , D ) = E y [ l o g D ( y ) ] + E x , z [ l o g ( 1 − D ( x , G ( x , z ) ) ) ] \mathcal{L}_{GAN}(G, D) = \mathbb{E}_{y}[logD(y)] + \mathbb{E}_{x, z}[log(1 - D(x, G(x, z)))] \tag{3} LGAN(G,D)=Ey[logD(y)]+Ex,z[log(1−D(x,G(x,z)))](3)
而更有效的方式是将GAN的指标和一些传统的损失结合起来,例如:L2 Distance,我们这里使用的是L1 Distance,因为相比起来它具有更少的模糊:
(4) L L 1 ( G ) = E x , y , z [ ∣ ∣ y − G ( x , z ) ∣ ∣ ] \mathcal{L}_{L1}(G) = \mathbb{E}_{x,y,z}[|| y-G(x, z)||] \tag{4} LL1(G)=Ex,y,z[∣∣y−G(x,z)∣∣](4)
最终我们的指标将会是这样的:
(5) G ∗ = arg min max L c G A N ( G , D ) + λ L L 1 ( G ) G^{*} = \arg\min\max\mathcal{L}_{cGAN}(G,D) + \lambda\mathcal{L}_{L1}(G) \tag{5} G∗=argminmaxLcGAN(G,D)+λLL1(G)(5)
对于输入的噪声向量z,即使没有这个噪声向量,神经网络依然可以学习到从x到y的输出映射,但是这是一个确定(deterministic)的结果!并且不会满足任何有价值的分布。
过去的一些做法是这样的:给生成器提供一个高斯噪声的输入。但是这种做法并不是特别有效,因为生成器通常会倾向于忽略这个噪声。
所以在最终的模型中,我们是利用dropout来提供这个噪声。
网络架构 Network Architecture
生成器和判别器都是使用: c o n v o l u t i o n − B a t c h N o r m − R e L u convolution-BatchNorm-ReLu convolution−BatchNorm−ReLu
生成器 —— 跳跃式生成器(Generator with skip)
如下图所示,可以看到,左边是传统的编码-解码网络(Encoder-Decoder Network)。这种网络的特点,我们也可以看到,所有的输入逐层经过整个网络:首先是经过逐层的下采样来到一个瓶颈区,然后再经过逐层的上采样。
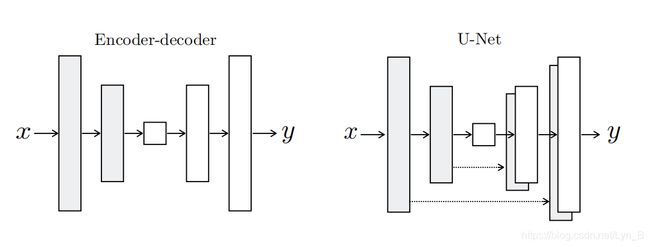
但是事实上,对于很多图像转换的问题,很多的图像低级特征都是相同的(比如,一些轮廓,直线和曲线)。也就是说,对于一些特征来说,它们并不需要再进入更深层的下采样层中,而是可以直接跨越网络到解码器对应的层去。
为了实现这样的功能,我们在网络中添加一种特殊的连接——跳跃连接(Skip Connection),也就变成了右边的网络:U型网络(U-Net)。
我们采用这样的方式添加skip:
(6) l a y e r i → l a y e r n − i layer_{i} \rightarrow layer_{n-i} \tag{6} layeri→layern−i(6)
每个连接会把 i i i 层的所有通道(channels)和 n − i n-i n−i 层的所有通道连接起来。
判别器 —— 马尔可夫判别器(Markovian Discriminator,PatchGAN)
patch,补丁,小片,对于在图像中,就是图像的一个局部小块。PatchGAN事实上就是针对图像的局部块(image patches),来进行损失的学习。它所要做的就是:判断一张图片的局部的 N × N N \times N N×N 块看起来是真的还是假的。
这个 N N N 值可以显著的小于图像的大小,并且仍然保证了一个高质量的输出,因为这样的PatchGAN显得更加精巧,有更少的参数,会有更快的运行速度,并且可以适用任意大小的图片。
PatchGAN对图像高频结构(high frequency structure)是非常有效的。
而对于低频结构(low frequency structure),我们之前提到, L 2 L2 L2 损失会导致输出模糊,( L 1 L1 L1也会,只是比起 L 2 L2 L2 它的模糊程度会比较好一些)而事实上,模糊其实就是很好的捕捉到图像的低频成分(滤去高频成分)。
所以,最后,我们会对PatchGAN输出的所有响应结果进行一个平均,来得到一个最终的结果。
优化和推断 Optimization & Inference
损失训练上,改为最大化判别器的输出:
(7) arg min log ( 1 − D ( x , G ( x , z ) ) ) → arg max log ( D ( x , G ( x , z ) ) ) \arg\min\log(1 - D(x, G(x, z))) \rightarrow\arg\max\log(D(x, G(x, z))) \tag{7} argminlog(1−D(x,G(x,z)))→argmaxlog(D(x,G(x,z)))(7)
并且在优化 D D D 的过程中,将指标除以 2 2 2 ,来减慢D相对于G的学习速率(防止过拟合?)。
在推断阶段,我们在测试(test time)中应用了 d r o p o u t dropout dropout,以及 b a t c h n o r m a l i z a t i o n batch\space normalization batch normalization,也就是前面提到的BatchNorm,这是一个利用统计特性进行归一化的过程,计算:
(8) x − m e a n v a r + ϵ \frac{x - mean}{\sqrt{var + \epsilon}} \tag{8} var+ϵx−mean(8)
其中 m e a n , v a r mean,var mean,var 和 ϵ \epsilon ϵ 都是当前测试批次的统计量:
- mean:均值
- var:方差
- ϵ \epsilon ϵ:防止方差为0的一个很小的正数
在实验过程中, b a t c h batch batch 的具体大小为 1 1 1 ~ 10 10 10,取决于具体的实验要求。
实验阶段 Experiment
我们通过一下工作来测试我们的方法,包括了图像处理,照片生成以及计算机视觉等:
- l a b e l s ↔ p h o t o labels\leftrightarrow photo labels↔photo,图像标签生成相应的照片
- A r c h i t e c t u r e l a b l e s ↔ p h o t o Architecture\space lables\leftrightarrow photo Architecture lables↔photo,结构化的标签生成照片
- M a p ↔ a e r i a l p h o t o Map \leftrightarrow aerial\space photo Map↔aerial photo,地图生成区域照片
- B W ↔ c o l o r p h o t o BW\leftrightarrow color\space photo BW↔color photo,黑白图像上色
- E d g e s → p h o t o Edges\rightarrow photo Edges→photo,边缘图像转化为照片
- S k e t c h → p h o t o Sketch\rightarrow photo Sketch→photo,素描转化为照片
- D a y → N i g h t Day\rightarrow Night Day→Night,白天照片转为夜间
- T h e r m a l → c o l o r p h o t o Thermal\rightarrow color\space photo Thermal→color photo, 红外线图像转为彩色照片
- P h o t o w i t h m i s s i n g p i x e l s → i n p a i n t e d p h o t o Photo\space with\space missing\space pixels\rightarrow inpainted\space photo Photo with missing pixels→inpainted photo,缺损图像修复
评估方法 —— Evaluation Metrics
- Amazon Mechanical Turk (AMT)
- FNC-Score
指标函数的分析 —— Analysis of Objective Function
我们通过一个对照实验,单独观察 L 1 L1 L1 和 cGAN的效果,同时也是比较条件生成对抗网络和非条件生成对抗网络之间的效果:
如图,我们发现,单独使用 L 1 L1 L1 时,出现了比较合理的结果,但是显得很模糊,而单独使用cGAN(即 λ = 0 \lambda = 0 λ=0)呈现出来的效果更加锐利,但是在视觉上引入了一些人工的成分。而当我们把这两者结合在一起使用时( λ = 100 \lambda = 100 λ=100),减少了人工成分,并且图像也不会显得模糊。
生成器结构的分析 —— Analysis of Generator Architecture
下图比较了传统的Encoder-Decoder和U-Net在城市景观图生成上的效果:

可以发现当两者都搭配 L 1 L1 L1 进行训练时,U-Net表现出了更好的效果
从PixelGAN到PatchGAN再到ImageGAN
我们测试 P a t c h Patch Patch 大小的不同的 N N N 值呈现出来的效果,从一个 1 × 1 1\times1 1×1的 像素级别的GAN(PixelGAN)到一个完整的 286 × 286 286\times286 286×286 的图像级别的GAN(ImageGAN)。
1 × 1 1\times1 1×1的PixelGAN并没有产生任何空域锐化的功能(因为只有一个像素),但是它再增加图像的彩度上有着明显的效果,例如下图:
可以看到,第一幅图是用 L 1 L1 L1 对我们的网络进行训练的,图片呈现出较为灰暗的效果。而采用 1 × 1 1\times1 1×1 的PixelGAN,你可以看到图片中的汽车呈现为红色。
而使用 $16\times 16 $ PatchGAN有效的实现了图像锐化,并且取得了不错的FNC-scores但是同时也显现出了一些不自然的成分; 70 × 70 70\times70 70×70 PatchGAN 则缓解了这种不自然的感觉,并且稍微提高了点分数;当我们最终提高到完整的 286 × 286 286\times286 286×286 ImageGAN 时,并没有想象中那样获得更好的图片效果,而且事实上取得了更低的FNC-score。这可能是因为ImageGAN更多的参数以及更大的深度增加了训练的难度,因此得到了一个不太理想的效果。
全卷积转换 Fully-convolutional translation
PatchGAN的还有一个优点,那就是一个固定大小的PatchGAN可以应用到任意大小的图片转换上。我们还可以将我们的生成器结合卷积,应用到比训练集更大的图片转换问题上。我们通过 M a p ↔ a e r i a l p h o t o Map \leftrightarrow aerial\space photo Map↔aerial photo 地图到区域照片的转换问题进行测试:
我们采用 256 × 256 256 \times 256 256×256 的图片训练我们的模型,然后应用到 谷歌地图 512 × 512 512\times512 512×512的分辨率上。可以看到对比度会调整呈现出清晰的图片。
知觉验证 Perceptual Validation
我们通过 M a p ↔ a e r i a l p h o t o Map \leftrightarrow aerial\space photo Map↔aerial photo 和 g r a y s c a l e ↔ c o l o r grayscale \leftrightarrow color grayscale↔color 这两个任务来测试我们的结果在现实感知上的效果:
Test M a p ↔ a e r i a l p h o t o Map \leftrightarrow aerial\space photo Map↔aerial photo

可以看到,采用 L 1 L1 L1(产生模糊效果)几乎不会欺骗到任何的实验参加者;而在地图到照片的转化工作上 L 1 + G A N L1+GAN L1+GAN成功欺骗了几乎 20 % 20\% 20% 的实验参加者。相反,我们可以看到,照片到地图上的转换两者相差不大,很少的实验参加者会被欺骗。这可能是因为,对于像地图这样较为工整简洁的结构上,一些微小的结构上的变化会显得较为的明显,而在显得一片混乱的城市照片上,我们很难去发现这些变化。
Test g r a y s c a l e ↔ c o l o r grayscale \leftrightarrow color grayscale↔color
我们通过ImageNet进行训练,最终我们的方法欺骗了 22.5 % 22.5\% 22.5% 的实验参加者,显然高于通过 L 2 L2 L2 进行损失训练的方法。但是很遗憾,相比于另一个论文的研究方法来说还是稍显不足,它欺骗了 27.8 % 27.8\% 27.8% 的参加者。。。

图像分割 Semantic Segmentation
我们可以发现,当输入到输出内容变得更加丰富,更加复杂时(例如,素描到照片的转换),我们的研究具有很好的效果。那么,当输出反而是变得更加简单,内容更少时,例如:图像分割问题,这样的计算机视觉问题,我们的研究的效果会怎样?
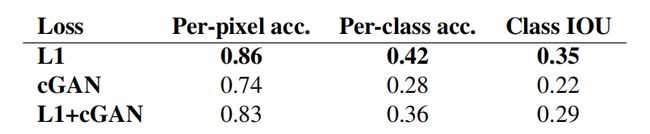
为了开始测试,我们训练了一个cGAN(结合 L 1 L1 L1,以及不结合 L 1 L1 L1)用于 p h o t o → l a b e l s photo \rightarrow labels photo→labels的问题,最终效果如下:

可以看到,乍一看,cGAN似乎也很好的完成了分割的工作,但是,事实上,仔细看时我们会发现,其中包含了很多细小的让人产生混乱的物体,而简单的利用 L 1 L1 L1 进行训练,则很好的解决了这个问题,从下表也可以看出, L 1 L1 L1 取得了更好的准确率和分数。
社区驱动调查 Community-driven Research
下面是在这篇论文发表之后,所带来的一些工作成果:







