数据结构与算法(2-2)线性表之链式存储(单链表、静态链表、循环链表、双向循环链表)
目录
一、单链表
1、存储方式
2、插入
3、删除
总代码:
二、静态链表
1、存储方式
2、插入
3、删除
4、遍历
总代码:
三、循环链表
总代码:
四、双向循环链表
1、存储方式:
2、插入和删除
3、正向遍历与反向遍历
总代码:
一、单链表
每个数据存储在结点中,单链表负责把这些结点串起来。(主要利用*next指针)
1、存储方式
从根结点开始(根结点可以不存储元素),用*next指针指向后面元素的地址,后面元素的*next继续指向更后面的元素,以此类推。(添加或插入元素要用malloc函数动态分配内存空间)头指针指向根,尾指针指向最后结点,便于插入删除。
//结点结构体
typedef struct Node
{
int data; //数据域
struct Node* next; //指针域
}Node;
Node* head;
Node* tail;2、插入
前面元素的*next断开,指向插入元素,插入元素的*next又指向后面的元素,完成“挤入”式插入。
//插入元素
void Insert(int index, int num)
{
int i = 0;
if (index < getLength() && index >= 0) //插入下标有效
{
Node* s = (Node*)malloc(sizeof(Node)), * p = head;
for (i = 0; i < index; i++)
p = p->next;
s->data = num; //插入的元素值
s->next = p->next; //s->后面
p->next = s; //前面->s
}
else
printf("不在插值范围内!");
}3、删除
待删除元素前面元素的*next断开,指向待删除元素后面的元素,释放掉待删除元素的空间。(前面malloc分配的内存需要释放)
//删除结点 (必须有外变量暂时保存要删除的结点)
//如果删除的是head结点,直接把head指向后面的结点即可
void Delete_Node(int index)
{
int i = 0;
Node* p = head, * s = NULL;
if (index < getLength() && index >= 0) //删除下标有效
{
for (i = 0; i < index; i++)
p = p->next; //移动到前一位
s = p->next; //要删除的结点
p->next = p->next->next; //前结点next->后结点(跳过要删除的结点)
free(s);
}
else
printf("没有该下标的结点!\n");
}总代码:
//单链表
//动态内存分配malloc函数: (指定的指针类型)malloc(要分配的字节数)
//头结点保存链表的首,可以在尾结点进行一系列操作(如添加),p表示动态的指针
#include
#include
int i = 0;
//结点结构体
typedef struct Node
{
int data; //数据域
struct Node* next; //指针域
}Node;
Node* head;
Node* tail;
//初始化链表
void Init_List()
{
//初始化链表
head = (Node*)malloc(sizeof(Node));
tail = (Node*)malloc(sizeof(Node));
head = tail;
}
//创建结点
void Add_Node(int Data)
{
Node* p = (Node*)malloc(sizeof(Node));
p->data = Data;
p->next = NULL;
//指针后移
tail->next = p;
tail = p;
}
//获取链表长度
int getLength()
{
int num = 0;
Node* p = head->next; //第一个数据存放在head->next里面
while (p)
{
num++;
p = p->next;
}
return num;
}
//遍历链表
void Print()
{
Node* p = head->next; //第一个数据存放在head->next里面
while (p)
{
printf("%d\n", p->data);
p = p->next;
}
}
//插入元素
void Insert(int index, int num)
{
int i = 0;
if (index < getLength() && index >= 0) //插入下标有效
{
Node* s = (Node*)malloc(sizeof(Node)), * p = head;
for (i = 0; i < index; i++)
p = p->next;
s->data = num; //插入的元素值
s->next = p->next; //s->后面
p->next = s; //前面->s
}
else
printf("不在插值范围内!");
}
//删除结点 (必须有外变量暂时保存要删除的结点)
//如果删除的是head结点,直接把head指向后面的结点即可
void Delete_Node(int index)
{
int i = 0;
Node* p = head, * s = NULL;
if (index < getLength() && index >= 0) //删除下标有效
{
for (i = 0; i < index; i++)
p = p->next; //移动到前一位
s = p->next; //要删除的结点
p->next = p->next->next; //前结点next->后结点(跳过要删除的结点)
free(s);
}
else
printf("没有该下标的结点!\n");
}
//清空链表
void Clear_List()
{
Node* p = head->next, * q;
while (p)
{
q = p->next;
free(p);
p = q;
}
head->next = NULL;
}
int main()
{
//初始化链表
Init_List();
//创建链表
for (i = 0; i < 5; i++)
{
Add_Node(i);
}
//插入结点
Insert(0, 5);
//删除结点(第二次删除注意:位置改变)
Delete_Node(0);
//清空链表
Clear_List();
//遍历
Print();
return 0;
}
二、静态链表
以数组的方式存储,虽然需要分配较大的内存空间,但是插入/删除比较容易,不需要移动数组元素,只用改变游标(cur)指向即可即可。
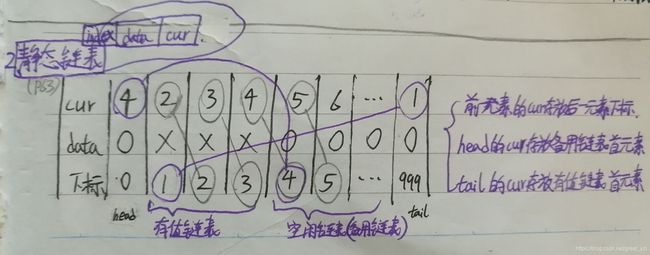
1、存储方式
创建一个数组(index是下标,cur是游标)
cur(游标):存放前一个元素的index,通过它实现连接。
整个链表被分成两部分:1、有值链表(存放有元素)2、备用链表(不存放元素)
首元素(index=0)的cur: 存放备用链表的首元素。
尾元素(index=MAXSIZE-1)的cur: 存放有值链表的首元素。
链表构成:1、以首元素为首构成的备用链表; 2、以尾元素为首构成的有值链表。
//静态链表结构体
typedef struct
{
int data; //数据
int cur; //游标
}StaticList;
StaticList L[MAXSIZE];2、插入
只移动游标,不移动元素。
//插入链表
void Insert(int index, int num)
{
int pre = MAXSIZE - 1;
if (index <= 0 || index > L[0].cur) //插入范围无效(第1个和最后一个元素不存放数据)
{
printf("%d Insert Error!\n", num);
return;
}
//移动到前一个元素(有效元素)
for (i = 1; i < index; i++)
pre = L[pre].cur;
L[0].cur = L[index].cur; //链表首元素游标指向备用链表首元素
L[index].data = num;
}3、删除
被删除的元素作为备用链表首元素,其游标连接原备用链表首元素,原备用链表首元素变成第二个元素(向后移)。
//删除链表(把需要删除的元素降级,变为备用链表的首元素)
void Delete(int index)
{
int pre = MAXSIZE - 1, j;
if (index < 1 || index >= L[0].cur)
{
printf("要删除的下标无效!\n");
return;
}
for (i = 1; i <= index - 1; i++)
pre = L[pre].cur; //移动到需要删除的前一个位置(有元素位)
L[index].cur = L[0].cur; //1、游标指向原备用元素(被删除的元素作为备用元素的首)
L[0].cur = index; //2、更新备用链表首元素(被删除的元素)
L[pre].cur = index; //3、连接前一个元素和后一个元素(游标)
}4、遍历
从index = MAXSIEZE-1处开始遍历(从尾元素开始遍历),因为尾元素的cur存有有效链表的首元素。
//遍历链表
void Traverse()
{
int cur;
cur = L[MAXSIZE - 1].cur; //指向有效链表的首元素
for (i = 1; i < L[0].cur; i++) //从第一个开始,到最后一个结束(备用链表的首元素就是最后一个元素的下一个元素)
{
printf("%d\n", L[cur].data);
cur = L[cur].cur; //有效链表中继续后移
}
}总代码:
//静态链表
//插入/删除时只修改游标,不移动结点
//游标存放下标,前一元素游标存放后一元素的下标
//第一个元素游标: 存放备用链表第一个元素的下标
//最后一个元素游标:存放有元素链表第一个元素的下标
//把有效元素作为一个循环,用pre=MAXSIZE-1标志开始,因为L[MAXSIZE-1].cur指向有效链表首元素,相当于在有效链表内循环
#include
#define MAXSIZE 20
int i = 0;
typedef struct
{
int data;
int cur;
}StaticList;
StaticList L[MAXSIZE];
//链表初始化
void List_Init()
{
//初始化游标
for (i = 0; i < MAXSIZE; i++)
{
L[i].cur = i + 1; //游标指向下一个
}
L[MAXSIZE - 1].cur = 1; //最后一个元素的游标(有效元素)
}
//根据游标获取下标(这里没用到)
int getIndex(int Cur)
{
for (i = 0; i < MAXSIZE; i++)
{
if (L[i].cur == Cur) //找到对应游标的元素
return i; //返回下标
}
return -1; //没有找到
}
//获取长度
int getLength()
{
int num = 0;
i = L[MAXSIZE - 1].cur;
if (L[0].cur == L[MAXSIZE - 1].cur) //没有元素
return 0;
while (i < L[0].cur)
{
i = L[i].cur;
num++;
}
return num;
}
//插入链表
void Insert(int index, int num)
{
int pre = MAXSIZE - 1;
if (index <= 0 || index > L[0].cur) //插入范围无效(第1个和最后一个元素不存放数据)
{
printf("%d Insert Error!\n", num);
return;
}
//移动到前一个元素(有效元素)
for (i = 1; i < index; i++)
pre = L[pre].cur;
L[0].cur = L[index].cur; //链表首元素游标指向备用链表首元素
L[index].data = num;
L[0].cur = L[index].cur; //更新备用链表
}
//删除链表(把需要删除的元素降级,变为备用链表的首元素)
void Delete(int index)
{
int pre = MAXSIZE - 1, j;
if (index < 1 || index >= L[0].cur)
{
printf("要删除的下标无效!\n");
return;
}
for (i = 1; i <= index - 1; i++)
pre = L[pre].cur; //移动到需要删除的前一个位置(有元素位)
L[index].cur = L[0].cur; //1、游标指向原备用元素(被删除的元素作为备用元素的首)
L[0].cur = index; //2、更新备用链表首元素(被删除的元素)
L[pre].cur = index; //3、连接前一个元素和后一个元素(游标)
}
//遍历链表
void Traverse()
{
int cur;
cur = L[MAXSIZE - 1].cur; //指向有效链表的首元素
for (i = 1; i < L[0].cur; i++) //从第一个开始,到最后一个结束(备用链表的首元素就是最后一个元素的下一个元素)
{
printf("%d\n", L[cur].data);
cur = L[cur].cur; //有效链表中继续后移
}
}
int main()
{
List_Init(); //链表初始化
printf("插入前元素总数:%d\n", getLength());
Insert(1, 6); //插入链表
Insert(2, 8);
Insert(3, 10);
printf("删除前元素总数:%d\n", getLength());
Delete(3);
Delete(2); //删除链表
Insert(2, 8);
printf("删除后元素总数:%d\n", getLength());
Traverse();
return 0;
} 三、循环链表
循环链表顾名思义,尾连接头,实现循环。
存储结构和链表类似,就多一个头尾相接,完成循环。
总代码:
//循环链表
//用了两个指针,一个指向头,一个指向尾,尾连接上头,完成循环链表
#include
#include
int i = 0;
//结构体
typedef struct Node
{
int data;
struct Node* next;
}Node;
Node* head; //头结点
Node* tail; //尾结点
Node* t; //遍历结点
//链表初始化
void List_Init()
{
head = (Node*)malloc(sizeof(Node)); //分配地址
tail = (Node*)malloc(sizeof(Node)); //分配地址
head->next = tail;
tail->next = head;
}
//获取链表长度
int getLength() {
int num = 0;
Node* L = head;
while (L->next != tail)
{
L = L->next;
num++;
}
return num;
}
//插入链表
void Insert(int index, int num)
{
if (index<0 || index>getLength())
{
printf("%d 序号不在范围内\n", num);
return;
}
Node* p = (Node*)malloc(sizeof(Node)), * L;
p->next = NULL;
L = head; //指向头
while (L->next != tail) //移动到尾结点前面(最后一个有效结点)
L = L->next;
L->next = p;
p->data = num;
tail = p->next; //更新尾结点
}
//删除链表
void Delete(int index)
{
if (index < 0 || index >= getLength())
{
printf("无该序号\n");
return;
}
Node* L = head, * t;
for (i = 0; i < index; i++)
L = L->next;
t = L->next;
L->next = L->next->next;
free(t);
}
//遍历链表
void Traverse()
{
Node* L = head;
while (L->next != tail) //头尾循环
{
L = L->next;
printf("%d\n", L->data);
}
}
int main()
{
List_Init(); //链表初始化
Insert(0, 0); //插入链表
Insert(1, 1);
Insert(2, 2);
Delete(2); //删除链表
Delete(1); //第二次删除位置改变
Traverse(); //遍历链表
return 0;
}
四、双向循环链表
双向循环链表优势:可以完成双向的遍历。
1、存储方式:
双向:*prior指针和*next指针分别指向前后两个元素。
循环:头结点的*prior指向尾结点,尾结点的*next指向头结点。
//双向循环链表
typedef struct Node
{
int data;
struct Node* prior;
struct Node* next;
}Node;2、插入和删除
插入:一个遍历链表,另一个进行插入(一开始不要进入链表,散置,不然会一直循环)。
删除:也要同时考虑next和prior指针。
3、正向遍历与反向遍历
正向遍历:从头结点head出发,向尾部遍历,直到遇到tail结束遍历。
反向遍历:从尾结点tail出发,向头部遍历,直到遇到head结束遍历。
//正向遍历链表
void Traverse()
{
Node* p = head;
printf("正向遍历:\n");
while (p->next != tail)
{
p = p->next;
printf("%d\n", p->data);
}
}
//反向遍历链表
void AntiTraverse()
{
Node* p = tail;
printf("反向遍历:\n");
while (p->prior != head)
{
p = p->prior;
printf("%d\n", p->data);
}
}总代码:
//双向循环链表
//前指针和后指针分别连接前面和后面的元素
//插入:一个遍历链表,另一个进行插入(一开始不要进入链表,散置,不然会一直循环)
//删除:也要同时考虑next和prior指针
#include
#include
//双向循环链表
typedef struct Node
{
int data;
struct Node* prior;
struct Node* next;
}Node;
Node* head; //头
Node* tail; //尾
int i = 0;
//链表初始化
void Init_List()
{
head = (Node*)malloc(sizeof(Node));
tail = (Node*)malloc(sizeof(Node));
head->prior = tail;
head->next = tail;
tail->next = head;
tail->prior = head;
//赋一个值,便于调试
tail->data = -2;
head->data = -1;
}
//获取元素数量
int getLength()
{
int num = 0;
Node* p = head;
while (p->next != tail)
{
p = p->next;
num++;
}
return num;
}
//链表插入
void Insert(int index, int num)
{
if (index<0 || index>getLength())
{
printf("插入下标不正确!\n");
return;
}
Node* t = (Node*)malloc(sizeof(Node)), * p;
p = head;
for (i = 0; i < index; i++)
{
p = p->next; //移动到前一个元素
}
t->prior = p;
t->next = p->next;
p->next->prior = t; //这一步要在前面
p->next = t; //这一步要在后面,负责p->next已经改变,前面的没有意义了
t->data = num;
}
//删除链表
void Delete(int index)
{
if (index < 0 || index >= getLength())
{
printf("删除下标不正确!\n");
return;
}
Node* p = head, * s;
for (i = 0; i < index; i++)
p = p->next;
s = p->next;
p->next->next->prior = p;
p->next = p->next->next;
free(s);
}
//正向遍历链表
void Traverse()
{
Node* p = head;
printf("正向遍历:\n");
while (p->next != tail)
{
p = p->next;
printf("%d\n", p->data);
}
}
//反向遍历链表
void AntiTraverse()
{
Node* p = tail;
printf("反向遍历:\n");
while (p->prior != head)
{
p = p->prior;
printf("%d\n", p->data);
}
}
int main()
{
Init_List(); //链表初始化
Insert(0, 0); //插入元素
Insert(1, 1);
Insert(2, 2);
Delete(2); //删除元素
Traverse(); //正向遍历
AntiTraverse(); //反向遍历
return 0;
}