python之逻辑回归项目实战——信用卡欺诈检测

1、项目介绍

\quad \quad 本项目通过利用信用卡的历史交易数据，进行机器学习，构建信用卡反欺诈预测模型，提前发现客户信用卡被盗刷的事件。

2、项目背景

\quad \quad 该项目所使用的数据集包含持卡人在两天内使用信用卡的交易情况，共有284807笔交易，其中有492笔交易为盗刷。数据集中的数据是经过了PCA降维，并且出于保密原因，这些特征都进行了脱敏处理，数据以秒为单位记录。通过对这些数据的分析，建模，可以对信用卡盗刷情况进行预测。有利于银行对存在风险的交易采取措施，减小银行和持卡人的损失。并设置合理的阈值，使得银行在减小盗刷损失的前提下，更好的提升使用信用卡的体验。

3、分析项目

\quad \quad 基于信用卡交易记录数据建立分类模型来预测哪些交易记录是异常的哪些是正常的。

4、数据读取与分析

4.1 加载数据

# 导入工具包
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# 魔法指令，在Notebook画图展示使用的
%matplotlib inline
data = pd.read_csv("creditcard.csv")
# 展示数据前前五行，查看数据
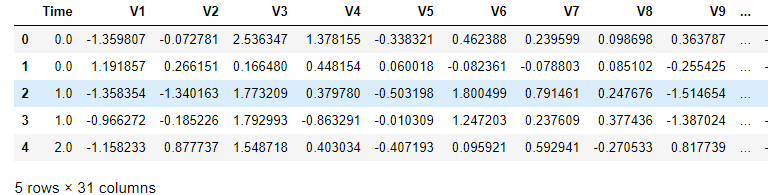
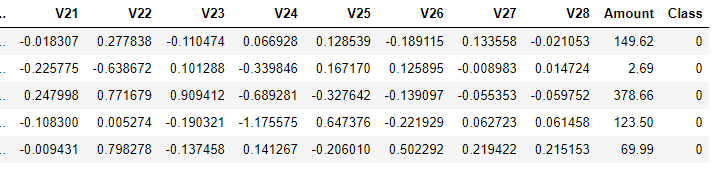
data.head()

此图为截取部分数据，原始数据集共有31列，其中数据特征有30列，Amount列表示贷款的金额（其数值变化幅度很大，后续处理时可进行标准化处理），Class列表示分类结果，若Class为0代表该条交易记录正常，若Class为1代表该条交易记录异常。

4.2 查看数据的标签分布

这里看看异常数据和正常数据各自的数量:

count_classes=pd.value_counts(data['Class'],sort=True).sort_index()
print(count_classes)
count_classes.plot(kind='bar')# 柱形图
plt.title("Fraud class histogram")
plt.xlabel("class")
plt.ylabel("Frequency")

out:
0 284315
1 492
Name: Class, dtype: int64

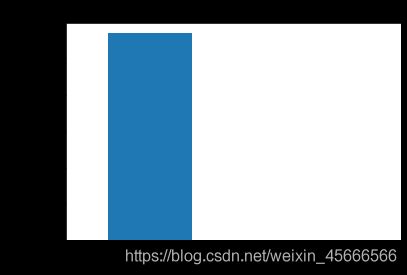
从图中可以看出标签为0的很多，而标签为1的却很少，说明样本的分布情况是非常不均衡的，所以在构建分类器的时候要特别注意一个误区，即使将结果全部预测为0也会出现很好的分类结果，这是在数据处理中需要着重考虑的一点。

5、数据预处理

5.1 特征标准化

1、首先对Amount的值进行标准化处理，从机器学习库Scikit-Learn引入标准化函数即可。

from sklearn.preprocessing import StandardScaler
# 在数据集中加入Amount标准化的一列数据,reshape(-1,1)的含义是将传入数据转换成一列的形式
data['normAmount']=StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
# drop操作去掉无用特征
data = data.drop(['Time','Amount'],axis=1)
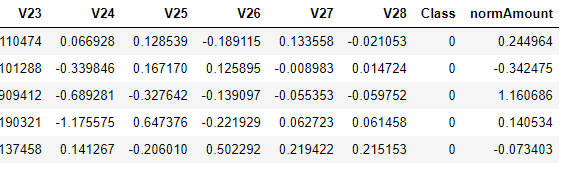
data.head()

5.2. 使用下采样解决样本数据不均衡

\quad \quad 首先计算异常样本的个数并取其索引，接下来在正常样本中随机选择指定个数样本，最后把所有样本索引拼接在一起即可。

#取出所有属性，不包含class的这一列
X = data.iloc[:, data.columns != 'Class']
#取出class这一列
y = data.iloc[:, data.columns == 'Class']


#计算出class==1（存在欺诈行为）元素有多少个
number_records_fraud = len(data[data.Class == 1])
# 得到所有异常样本的索引
fraud_indices = np.array(data[data.Class == 1].index)

# 得到所有正常样本的索引
normal_indices = data[data.Class == 0].index

# 在正常样本中随机采样出指定个数的样本，并取其索引
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
# 转换成numpy的格式
random_normal_indices = np.array(random_normal_indices)

# 有了正常和异常样本后把它们的索引都拿到手，将class=0和1的样本的索引拼接在一起
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])

# 根据索引得到下采样所有样本点
under_sample_data = data.iloc[under_sample_indices,:]
#下采样数据集的数据
X_undersample = under_sample_data.iloc[:, under_sample_data.columns != 'Class']
#下采样数据集的label
y_undersample = under_sample_data.iloc[:, under_sample_data.columns == 'Class']

# 下采样 样本比例
print("正常样本所占整体比例: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("异常样本所占整体比例: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("下采样策略总体样本数量: ", len(under_sample_data))

输出结果

正常样本所占整体比例:  0.5
异常样本所占整体比例:  0.5
下采样策略总体样本数量:  984

6、训练数据即划分数据集

疑问？ 为什么进行了下采样，还要把原始数据进行切分呢？
这是因为 对数据集的训练是通过下采样的训练集，对数据的测试的是通过原始的数据集的测试集，下采样的测试集可能没有原始部分当中的一些特征，不能充分进行测试。

from sklearn.model_selection import train_test_split

# 整个数据集进行划分
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)

print("原始训练集包含样本数量: ", len(X_train))
print("原始测试集包含样本数量: ", len(X_test))
print("原始样本总数: ", len(X_train)+len(X_test))

# 下采样数据集进行划分
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample
                                                                                                   ,y_undersample
                                                                                                   ,test_size = 0.3
                                                                                                   ,random_state = 0)
print("")
print("下采样训练集包含样本数量: ", len(X_train_undersample))
print("下采样测试集包含样本数量: ", len(X_test_undersample))
print("下采样样本总数: ", len(X_train_undersample)+len(X_test_undersample))

7、模型建立

7.1 sklearn LR工具包

官方文档

class 
sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, 
random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)

7.2 模型调参，初步建立模型

1、正则化惩罚参数调一调

\quad \quad 使用逻辑回归模型构建分类器，通过k折交叉验证寻找最优正则化惩罚参数C。

\quad \quad 由于本文数据的特殊性，分类模型的评估的方法十分钟重要，通常采用的评价指标有准确率、召回率和F值（F-Measure）等。本文采用recall（召回率）作为评估标准。原因是具体举个例子介绍：假设我们在医院中有1000个病人，其中990个为正样本（正常），10个为负样本（癌症），我们的目的是找出其中的10个负样本，假如我们的模型将多有的1000个病人都预测为正样本，虽然精度有99%，但是并没有找到我们所要的10个负样本，所以这个模型是没用的，因为一个癌症病人都找不出来。而recall是对于想找的东西，找到了多少个，而不是所有样本的精度。
\quad \quad 在构造权重参数的时候，为了防止过拟合的现象发生，要引入正则化惩罚项，使这些权重参数处于比较平滑的趋势，具体参数选择在代码中会给出解释。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold,cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report
def printing_Kfold_scores(x_train_data,y_train_data):
    #k折交叉验证
    fold = KFold(n_splits=5,shuffle=False)
    #不同的惩罚参数C的参数集，因为不知道哪一种惩罚参数的力度好，通过验证集结果来选择
    c_param_range = [0.01,0.1,1,10,100]
    #创建一个5行两列的空的DataFrame框，用于存放数据
    results_table = pd.DataFrame(index = range(len(c_param_range),2), columns = ['C_parameter','Mean recall score'])
    #将'C_parameter'列设置为惩罚参数集中的值
    results_table['C_parameter'] = c_param_range
    #k折操作将会给出两个列表：train_indices = indices[0], test_indices = indices[1]
    j = 0
    for c_param in c_param_range:
        print('-------------------------------------------')
        print('C parameter: ', c_param)
        print('-------------------------------------------')
        print('')
        recall_accs = []
        #enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。
        for iteration,indices in enumerate(fold.split(x_train_data)):
            #把c_param_range代入到逻辑回归模型中，并使用了l1正则化
            lr = LogisticRegression(C = c_param,penalty = 'l1',solver='liblinear')
            #使用indices[0]的数据进行拟合曲线，使用indices[1]的数据进行误差测试
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
            #在indices[1]数据上预测值
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
            #根据不同的c_parameter计算召回率
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
            recall_accs .append(recall_acc)
            print('Iteration ', iteration,': recall score = ', recall_acc)
        #求出我们想要的召回平均值
        results_table.loc[j,'Mean recall score'] = np.mean(recall_accs)
        j += 1
        print('')
        print('Mean recall score ', np.mean(recall_accs))
        print('')
    best_c = results_table.loc[results_table['Mean recall score'].values.argmax()]['C_parameter']
    #最后选择最好的 C parameter
    print('*********************************************************************************')
    print('Best model to choose from cross validation is with C parameter = ', best_c)
    print('*********************************************************************************')
    return best_c
#交叉验证与不同参数结果
best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)

输出结果：

-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration  0 : recall score =  0.9315068493150684
Iteration  1 : recall score =  0.9178082191780822
Iteration  2 : recall score =  1.0
Iteration  3 : recall score =  0.972972972972973
Iteration  4 : recall score =  0.9545454545454546

Mean recall score  0.9553666992023157

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration  0 : recall score =  0.8493150684931506
Iteration  1 : recall score =  0.863013698630137
Iteration  2 : recall score =  0.9322033898305084
Iteration  3 : recall score =  0.9459459459459459
Iteration  4 : recall score =  0.9090909090909091

Mean recall score  0.8999138023981302

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration  0 : recall score =  0.863013698630137
Iteration  1 : recall score =  0.863013698630137
Iteration  2 : recall score =  0.9661016949152542
Iteration  3 : recall score =  0.9459459459459459
Iteration  4 : recall score =  0.8939393939393939

Mean recall score  0.9064028864121736

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration  0 : recall score =  0.8767123287671232
Iteration  1 : recall score =  0.8767123287671232
Iteration  2 : recall score =  0.9661016949152542
Iteration  3 : recall score =  0.9324324324324325
Iteration  4 : recall score =  0.9090909090909091

Mean recall score  0.9122099387945685

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration  0 : recall score =  0.8767123287671232
Iteration  1 : recall score =  0.9041095890410958
Iteration  2 : recall score =  0.9661016949152542
Iteration  3 : recall score =  0.9324324324324325
Iteration  4 : recall score =  0.9090909090909091

Mean recall score  0.9176893908493631

*********************************************************************************
Best model to choose from cross validation is with C parameter =  0.01
*********************************************************************************

从输出结果中可以看出最佳的惩罚参数C为0.01。

8、模型评估

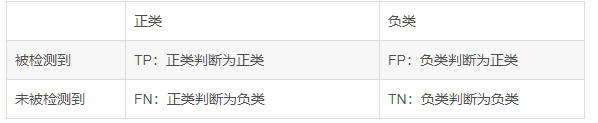
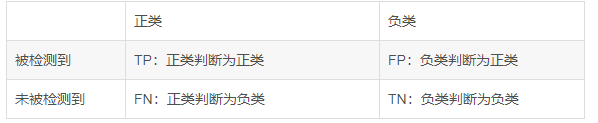
8.1 分类模型常用评估方法

1、 准确度
\quad \quad 表示在分类问题中，做对的占总体的百分比
$$Accuracy=\frac{TP+TN}{TP+FP+FN+TN}$$

2、 召回率
\quad \quad 表示在正例中有多少能预测到，覆盖面的
大小，一般作为检测类题目的评估标准。简言之，就是实际筛选出来的/本应该筛选出来的。

$$Recall=\frac{TP}{TP+FN}$$

3、精确度
\quad \quad 表示被分为正例中实际为正例的比例。

$$Precision=\frac{TP}{TP+FP}$$

4 、混淆矩阵

代码

# 混淆矩阵的可视化显示，以下代码可以直接作为模板
import itertools
def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    绘制混淆矩阵
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

8.2 模型评估——混淆矩阵

1、使用下采样数据训练，使用下采样数据测试

# 下采样最佳参数构造的LR模型
lr = LogisticRegression(C = best_c, penalty = 'l1',solver='liblinear')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)
#计算混淆矩阵，confusion_matrix(y_true,y_pred)
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
#输出精度为小数点后两位
np.set_printoptions(precision=2)
print("召回率: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
#画出非标准化的混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,classes=class_names,title='Confusion matrix')
plt.show()

输出结果：

召回率:  0.9387755102040817

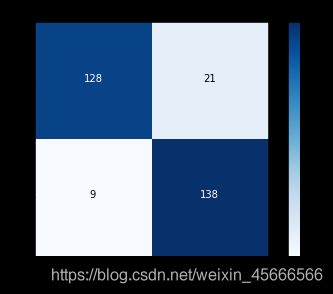
\quad \quad 在下采样数据集中，目标任务是二分类，所以只有0和1，主对角线上的值就是预测值和真实值一致的情况，深色区域代表模型预测正确（真实值和预测值一致），其余位置代表预测错误。数值9代表有9个样本数据本来是异常的，模型却将它预测为正常，相当于“漏检”。数值21代表有21个样本数据本来是正常的，却把它当成异常的识别出来，相当于“误杀”。

\quad \quad 最终得到的召回率为0.93878，看起来是一个还不错的指标，但是还有一些问题。用下采样的数据集进行建模，并且测试集也是下采样的测试集，在这份测试集中，异常样本和正常样本的比例基本均衡，因为已经对数据集进行过处理。但是实际的数据集并不会是这样的，相当于在测试使用理想情况来代替真实情况，这样的检测效果可能会偏高。因此，我们在测试的时候，千万要注意使用原始数据的测试集，才能最具有代表性，只需要改变传入的测试数据即可。下面来操作一下：

2、使用下采样数据训练，使用原始数据测试

lr = LogisticRegression(C = best_c, penalty = 'l1',solver='liblinear')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)
#计算混淆矩阵
cnf_matrix = confusion_matrix(y_test,y_pred)
#输出精度为小数点后两位
np.set_printoptions(precision=2)
print("召回率: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
#画出非标准化的混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,classes=class_names,title='Confusion matrix')
plt.show()

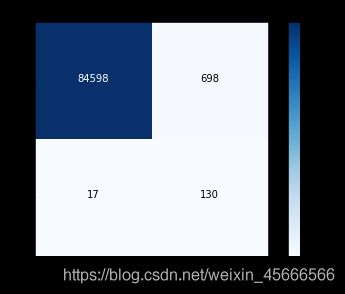
输出结果：

召回率:  0.9251700680272109

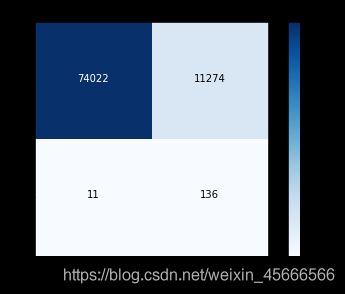
\quad \quad 虽然recall值可达到92.5%，但是其中有11274个数据本来不存在欺诈行为，却检测成了欺诈行为，这还是一个挺头疼的问题。如果误杀掉这么多样本，实际业务也会出现问题，这就要求我们再对模型进行修改。之前我们所提到的解决样本不均衡方案还有一个过采样方案，下面我们来试一下。

9、改进模型——过采样方案

\quad \quad 在下采样方案中，虽然得到较高的召回率，但是误杀的样本数量太多了，下面就来看看用过采样方案能否解决这个问题。使用过采样，使得两种样本数据一样多。

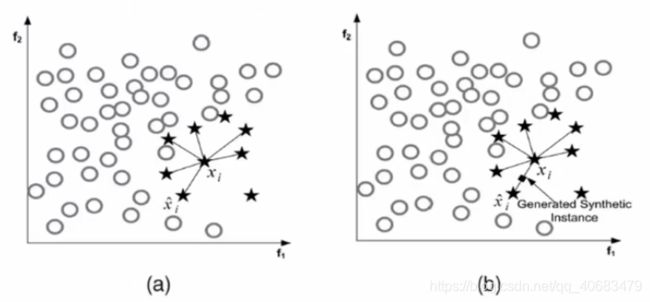
9.1 SMOTE数据生成策略

\quad \quad 如何才能让异常样本与正常样本一样多呢？这里需要对少数样本进行生成，这可不是复制粘贴，一摸一样的样本是没有用的，需要采用一些策略，最常用的就是SMOTE算法，其基本原理为：
1、对于少数类中的每一个样本x，以欧式距离计算它到少数类样本集中所有样本的距离，经过排序，得到其近邻样本。

2、根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数样本x，从其近邻中开始依次选择N个样本$x_n$。

3、对于每一个选出的近邻样本，分别与原样本按照如下的公式构建新的样本。
$$x_{new}=x+rand(0,1)\ast (x_n-x)$$

\quad \quad 对于SMOTE算法，可以使用imblearn工具包完成这个操作，首先需要安装该工具包，可以直接在命令行中使用pip install imblearn 完成安装操作。再把SMOTE算法加载进来，只要将特征数据和便签传进去即可。

9.2 构造过采样数据

import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
# 读入文件，将数据分成features-labels两部分
credit_cards=pd.read_csv('creditcard.csv')
columns=credit_cards.columns
# 在特征中去除掉标签
features_columns=columns.delete(len(columns)-1)
features=credit_cards[features_columns]
labels=credit_cards['Class']
# 划分训练集、测试集
features_train, features_test, labels_train, labels_test = train_test_split(features, 
                                                                            labels, 
                                                                            test_size=0.3, 
                                                                            random_state=0)
# 过采样
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)
len(os_labels[os_labels==1])#查看生成样本后异常样本的数量

9.3 构建模型

1、 K折交叉验证得到最好的惩罚参数C

# 转换成能被逻辑回归模型接受的数据类型
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
# 带入前面写好的交叉验证调参函数得到最优参数
best_c = printing_Kfold_scores(os_features,os_labels)

输出结果：

-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration  0 : recall score =  0.9142857142857143
Iteration  1 : recall score =  0.88
Iteration  2 : recall score =  0.9716742539200809
Iteration  3 : recall score =  0.9614732372781288
Iteration  4 : recall score =  0.9618752119788461

Mean recall score  0.9378616834925542

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration  0 : recall score =  0.9142857142857143
Iteration  1 : recall score =  0.88
Iteration  2 : recall score =  0.9728376327769348
Iteration  3 : recall score =  0.9640735111233937
Iteration  4 : recall score =  0.9641111962515859

Mean recall score  0.9390616108875257

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration  0 : recall score =  0.9142857142857143
Iteration  1 : recall score =  0.88
Iteration  2 : recall score =  0.9730652503793626
Iteration  3 : recall score =  0.9644001155677264
Iteration  4 : recall score =  0.9644001155677264

Mean recall score  0.939230239160106

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration  0 : recall score =  0.9142857142857143
Iteration  1 : recall score =  0.88
Iteration  2 : recall score =  0.9730905412240769
Iteration  3 : recall score =  0.9642870601831497
Iteration  4 : recall score =  0.9642242516361627

Mean recall score  0.9391775134658207

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration  0 : recall score =  0.9142857142857143
Iteration  1 : recall score =  0.88
Iteration  2 : recall score =  0.9726858877086495
Iteration  3 : recall score =  0.9643624304395342
Iteration  4 : recall score =  0.9644252389865213

Mean recall score  0.9391518542840839

*********************************************************************************
Best model to choose from cross validation is with C parameter =  1.0
*********************************************************************************

2、逻辑回归计算混淆矩阵以及召回率

# 代入逻辑回归模型计算混淆矩阵以及召回率

lr = LogisticRegression(C = best_c, penalty = 'l1',solver='liblinear')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)
# 计算混淆矩阵
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# 画出非规范化的混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

输出结果：

Recall metric in the testing dataset:  0.8843537414965986

\quad \quad 小结：虽然过采样的recall值比下采样稍小，但是它的精度却大大提高了，即减少了误杀的数量，所以在出现数据不均衡的情况下，较经常使用的是生成数据而不是减少数据，但是数据一旦多起来，运行时间也变长了。

10、总结

从此项目中得到了以下技术点：

10.1 样本不均衡解决方案

\quad \quad 如何解决数据标签不平衡问题？首先造成数据标签不平衡的最根本原因就是它们的个数相差悬殊，如果能让它们的个数相差不大，或者比例接近，这个问题就解决了。基于此，有以下两种解决方案：

（1）下采样
\quad \quad 既然异常数据比较少，那就让正常样本和异常样本一样少。例如正常样本有30w个，异常样本只有500个，若从正常样本中随机选出500个，他们的比列就均衡了。虽然下采样的方法看似很简单，但是也存在瑕疵，即使原始数据很丰富，下采样过后，只利用了其中一小部分数据，这样对结果会不会有影响呢？

（2）过采样
\quad \quad 不想放弃任何有价值的数据，只能让异常样本和正常样本一样多，怎么做到呢？异常样本样本若只有500个样本，此时可以对数据进行和转换，假造出来一些异常数据，数据生成也是现阶段常见的一种套路。虽然数据生成解决了异常样本数量的问题，但是异常数据毕竟是造出来的，会不i会存在问题呢？

\quad \quad 这两种方案各有优缺点，到底哪种方案比较好呢？需要进行实验比较。

10.2 其他

（1）模型的调参也是很重要的，之前我们通过实验也发现了不同的参数可能会对结果产生较大的影响，这一步也是必须的，后续实战内容我们还会来强调调参的细节，这里就简单概述一下了。对于参数我建立大家在使用工具包的时候先看看其API文档，知道每一个参数的意义，再来实验选择合适的参数值。

（2）得到的结果一定要和实际任务结合在一起，有时候虽然得到的结果指标还不错，但是实际应用却成了问题，所以测试环节也是必不可少的。到此，这个项目就给大家介绍到这里了，在实践中学习才能成长的更快，建议大家一定使用提供的Notebook代码文件来自己完成一遍上述操作。