数据结构与算法(java):线性表-队列
队列
1、概述
1.1 定义
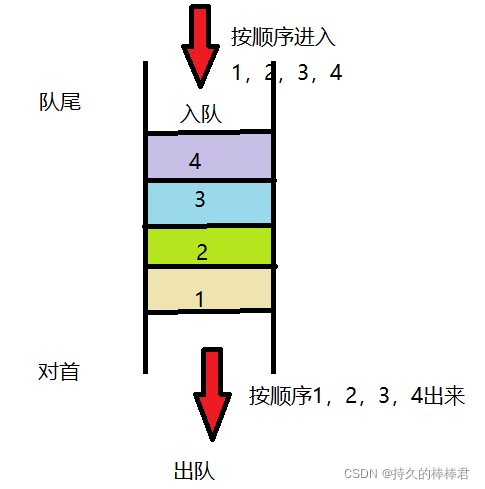
队列是一种基于先进先出(FIFO)的数据结构,是一种特殊线性表,也称先进先出表。插入和删除操作只能分别在其两端进行,根据先进先出的原则存储数据,先进入的数据在读取数据时先被读出来。把插入元素的过程称为入队(Equeue),插入元素的一端称为队尾(rear),删除元素的过程称为出队(Dequeue),删除元素的一端称为对首(front),没有任何元素的队列称为空队。
1.2 图示
2、分类
顺序结构存储的队列:顺序队
链式结构存储的队列:链队
2.1 顺序队列
2.1.1 图示、实现步骤及各方法思路
关于顺序队列,其实还可以分为顺序非循环队列和顺序循环队列,用的相对较多的是后者,我这里只讲解循环队列就行,至于为什么选择循环队列,可以比较下面几幅图。。。
假设这个队列最多能存储5个元素
图示如下
图二 顺序循环队列
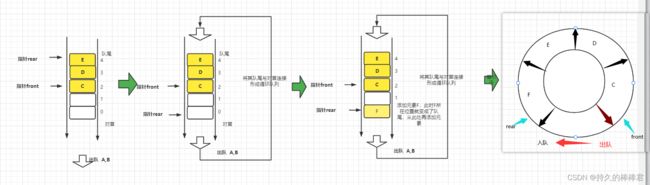
可以发现,非循环队列元素全部出队后,两指针全部指向了队尾,原来的一片空间不能再利用,造成了空间浪费,这也叫假溢出,而循环队列可以很好的解决这个问题。
循环队列,也叫环形队列,它是把数组的前后部分连接起来形成一个循环数组,构成一个环,每次出队后可以空出一片空间,可以再次利用这片空出来的空间存储元素。
实现步骤
1、创建队列类(可以实现Queue接口,随自己),定义变量(数组,队列最大值maxSize,两指针front和rear),实现构造方法
2、实现各个方法,包括基本的入队,出队,判断队尾是否为空或满了,队列的大小,队列中元素个数,是否需要扩容等等
各方法分析
(1)指针的作用:定义了两个指针front和rear,非循环队列初始值均为-1,计算循环队列时初始值均为0,通过变换他两的指向来控制出队和入队
(2)观察图时可以发现,当rear==front时既能表示队列为空或者队列已满,怎么区分开来呢,可以如下
- 判断循环队列是否为空:约定rear==front表示队列为空
- 判断循环队列是否已满:
- 方法一:设置一个标志位flag,默认值为true,每当指针rear或者指针front的指向从下标maxSize-1到0时将flag取反,即flag=!flag,每当flag= =false&&front= =rear时表示栈已满
- 方法二:牺牲一个数组地址空间,不存放任何元素,这片空间是动态的,主要的作用避免与队列空的条件front= =rear一致,通过判断是否(rear+1)%maxSize= =front来判定队列是否满了,
如:先将元素A~D按字母顺序依次添加到队列中,并且从队首删除A,B,空出两片地址空间,此时front指向数组data[1],rear指针指向了队尾data[3],之后通过循环队列继续添加元素E,rear经循环后重新指向data[0],此时指针front所指的位置留出一片空间,不再添加元素,主要用于避免与队列空的条件front=rear一致,当front=(rear+1)/maxsize,即1 = (0+1)%4 ,此时就可以判定队列已经满了。

此外还需注意指针front,rear下标的取值范围是0~size-1,确保循环利用存储单元,需更新指针指的位置,因此有如下计算关系
front = (front+1)%maxSize;
rear = (rear + 1) %maxSize;
(3)入队方法:将rear指针指向下一个空元素的位置,注意判断队列是否满队,如果不嫌麻烦的话还可以决定满队后是否需要扩容
(4)出队方法:将front指针指向下一个的非空元素,删除该元素并且返回被删除的该元素(也就是此时的队首元素),期间需要判断队列是否为空,为空返回null
(5)清除队列所有元素:将元素遍历全部设置为null,两指针重新指向数组下标为0的位置,队列长度maxSize置为0
。。。
2.1.2 代码实现
import java.util.NoSuchElementException;
public class SeqQueue<T> {
private T elements[]; //存储数据的数组
private int front, rear; //分别存放队头指针和队尾指针
private int Num; //元素实际个数
//构造方法
public SeqQueue() {
this(6);
}
public SeqQueue(int capacity) {
this.elements = (T[]) new Object[capacity];
this.front = 0;
this.rear = 0;
this.Num = 0;
}
//------------------------------------------------------------
//返回队列中实际元素个数
public int size(){
return this.Num;
}
//判断队列是否为空
public boolean isEmpty(){
return front == rear;
}
//------------------------------------------------------------
//判断队列是否满了
public boolean isFull(){
if(this.front == (this.rear + 1)%this.elements.length){
return true;
}
return false;
}
//------------------------------------------------------------
//出队操作(执行删除操作,并返回删除元素)
public T Dequeue(){
if(isEmpty()){
throw new NoSuchElementException("The SeqQueue is empty!");
// return null; //或者返回null
}
front = (front + 1) % elements.length;
Num--;
return elements[front];
}
//------------------------------------------------------------
//入队操作(不扩容)
public void Enqueue(T t){
if(isFull()){
throw new IndexOutOfBoundsException("The SeqQueue is full!");
}
this.rear = (this.rear + 1)%this.elements.length;
Num++;
elements[rear] = t;
}
//------------------------------------------------------------
//入队操作,队列已满,但还想添加元素时,进行扩容
public void EnqueueAndCapEnlarge(T t){
if(isFull()){
ensureCapacity(elements.length+1);
}
this.rear = (this.rear + 1)%this.elements.length;
Num++;
elements[rear] = t;
}
//------------------------------------------------------------
//清空队列
public void Clear(){
for(int i = this.front; i != this.rear; i=(i+1)%elements.length){
elements[i] = null;
}
this.front = this.rear = 0;
this.Num = 0;
}
//------------------------------------------------------------
//查看队头元素
public T searchFirst(){
if(isEmpty()){
throw new NoSuchElementException("The SeqQueue is empty!");
// return null;
}
return elements[(front+1)%elements.length];
}
//------------------------------------------------------------
public void ensureCapacity(int capacity){
//capacity是新的队列长度,比原队列长度小时不扩容,
if(capacity < elements.length){
return ;
}
//声明新数组引用指向原数组,存储的是原来数组的值
T[] newArray = elements;
//利用原数组的引用创建新数组
elements = (T[]) new Object[capacity];
//复制原数组中的元素到新数组中
int j = 0;
for(int i = this.front; i!= this.rear; i=(i+1)% newArray.length){
elements[j++] = newArray[i];
}
//指针重新指向
this.front = 0;
this.rear = j;
}
}
测试类
public class SeqQueueTest {
public static void main(String[] args) {
SeqQueue<String> sq = new SeqQueue<>(7);
sq.Enqueue("tencent");
sq.Enqueue("tik tok");
sq.Enqueue("alibaba");
sq.Enqueue("oppo");
sq.Enqueue("xiaomi");
sq.Enqueue("huawei");
// sq.Enqueue("apple"); //IndexOutOfBoundsException
sq.EnqueueAndCapEnlarge("apple");
System.out.println(sq.size());
System.out.println(sq.Dequeue());
System.out.println(sq.Dequeue());
System.out.println(sq.size());
System.out.println(sq.searchFirst());
}
}
结果如下
7
tencent
tik tok
5
alibaba
2.2 链式队列
2.2.1 图示及原理分析,方法分析
原理分析
对于链式队列,用到的是单链表实现,因为单链表只要增加队首指针和队尾指针就可以轻松访问头尾结点,时间复杂度很低(O(1)),而双链表会的空间开销很大(空间复杂度高,很多前继指针),所以不采用双链表。如图:
图示
我们定义两个结点,头结点head和尾结点last,两者默认指向为null,当队列添加第一个元素时,令头结点指向新添加元素,尾结点也指向新添加元素
(1)入队操作时,令尾结点last指向新添加那个元素,作为新的尾结点
(2)出队操作时,改变头结点的指向,令其指向队首元素的下个元素,作为新的队首元素(需要注意的是头结点并非是队首元素),此时原队首元素就出队了
方法分析
(1)初始化队列时,头结点和尾结点均指向null,即head=last=null,且条件last==null成立时表示队列为空;
(2)出队操作时,判断队列是否为空,不为空,则获取队首结点元素,删除队首结点并返回该节点,期间要做的是改变指针head的指向,将其指向原队首元素的下一个结点,即head=head.next;
(3)入队操作时(注意链队并不需要判断是否队列已满),当队列为空时,新增的结点就是尾结点last,令头结点指向当前尾结点;当队列不为空时,令原尾结点指向新增的元素,并且新增的元素成为新的尾结点
2.2.2 代码实现
import java.util.Iterator;
public class LinkedQueue<T> implements Iterable<T>{
private Node head,last; //记录首结点和尾结点
private int Num; //队列中的元素个数
private class Node{
public T item;
public Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
public LinkedQueue(){
this.head = new Node(null,null);
this.last = null;
this.Num = 0;
}
//-------------------------------------------------
//判断队列是否为空
public boolean isEmpty(){
return Num==0;
}
//-------------------------------------------------
//队列中元素个数
public int size(){
return Num;
}
//-------------------------------------------------
//入队操作
public void Enqueue(T t){
if(last == null){
//尾结点last==null
last = new Node(t,null);
head.next = last;
}else{
//当前尾结点last不为null
Node oldLast = last;
last = new Node(t,null);
oldLast.next = last;
}
Num++;
}
//-------------------------------------------------
//出队操作
public T Dequeue(){
if(isEmpty()){
return null;
}
Node oldFirst = head.next;
head.next = oldFirst.next;
Num--;
//当队列元素全部删完时,重置last=null
if(isEmpty()){
last=null;
}
return oldFirst.item;
}
//-------------------------------------------------
@Override
public Iterator<T> iterator() {
return new SQIterator();
}
private class SQIterator implements Iterator{
private Node n;
public SQIterator(){
this.n = head;
}
@Override
public boolean hasNext() {
return n.next!=null;
}
@Override
public Object next() {
n = n.next;
return n.item;
}
}
}
测试类
public class LinkedQueueTest {
public static void main(String[] args) {
LinkedQueue<String> lq = new LinkedQueue<>();
lq.Enqueue("hello");
lq.Enqueue("world");
System.out.println(lq.size());
for(String obj : lq){
System.out.println(obj);
}
lq.Dequeue();
System.out.println(lq.size());
}
}
结果
2
hello
world
1