约束满足问题(Constraint Satisfaction Problems——CSPs):回溯操作,向前检验,约束传播,局部搜索
文章目录
- 前言
- 一、约束满足问题是什么?
- 二、CSP问题的回溯搜索
-
- 回溯搜索(Backtracking search)
- 选择变量的策略一:MRV启发式
- 选择变量的策略二:度(degree)启发式
- 选择变量的策略三:最少约束值(Least constraining value)启发式
- 向前检验(Forward checking)
- 约束传播(Constraint propagation):
- 三,CSP问题的局部搜索(Local search for CSPs)
- In conclusion
前言
约束满足问题
CSP问题的回溯搜索
约束满足问题的局部搜索
提示:以下是本篇文章正文内容,下面案例可供参考
一、约束满足问题是什么?
约束满足问题包含一组变量和一组变量间的约束。找到所有变量的一个(或多个)赋值,使所有约束都得到满足。
举一个经典的例子:澳洲版图的颜色填充( Map-Coloring)
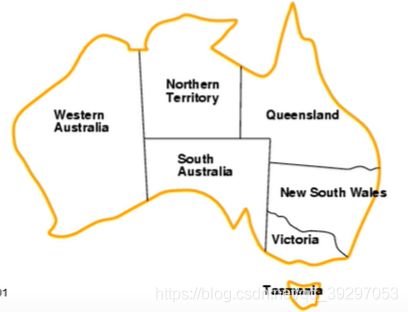
变量集合是各个州郡的单词简写:WA,NT,Q,NSW,V,SA,T
值域:D={red,green,blue}
约束:相邻域的颜色不同
以上就是经典的约束满足问题的例子:颜色填充
下图则是该问题所有解中的一个

为了方便解题,可以将地图转换成约束图(Constraint graph)的方式:节点表示变量,弧表示约束。如下图所示:
ps:约束分为绝对约束和偏好约束两个等级,绝对约束要求任何违反规则的都排除在解之外;偏好约束指出哪些解是更偏好的。

二、CSP问题的回溯搜索
回溯搜索(Backtracking search)
回溯搜索与深度优先搜索概念上非常相似:
但是在DFS中,我们假定通过应用所有可能的操作将节点添加到边缘来扩展节点(然后,如果需要,这些节点将位于边缘上,准备进一步扩展)
回溯搜索仅需执行一个操作即可生成一个后继节点,然后继续向下操作(然后,如果需要,随后返回该节点,将检查是否可以生成其他任何后继节点。
针对填色问题的回溯描述

如图,对版图随机挑选一个州进行随机着色,当程序走到图中最下层时出现一个问题,如果程序选择红色框起来的选项,那么在对中下部分的州,进行下一层的着色时发现,没有哪一种颜色可以符合两个州郡之间颜色不一样这一约束的。
这时程序将返回到红色框圈起来的这一步,并选择与其在同一层的蓝色圆圈的选择,这一当尝试选择失败,返回上一级,对上一级重新做选择的操作成为回溯操作。
需要注意的是,一般回溯是顺序试探,可能无用,应有一定的策略避免无用搜索。
在回溯搜索中,我们可以发现四个问题:
1,下一步选什么变量?按什么顺序尝试它的值?
2,如何减少搜索空间?
3,当前变量与未赋值变量的关系是什么?
4,如何避免失败,即当一条路径失败时,搜索后面的路径如何避免这种失败
下面我们以此解决这些问题
选择变量的策略一:MRV启发式
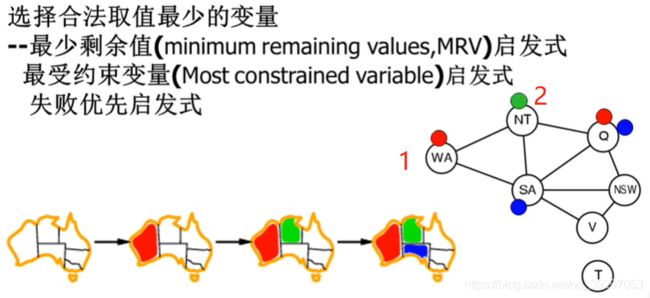
如图,当我们走完第一步和第二部时,在选择SA为第三步还是Q为第三步,首先分析可供SA和Q选择的颜色数量,我们发现Q有两种颜色可选,而SA只有一种。所以MRV启发式通过优先选择最少剩余量的选项来做出正确选择。
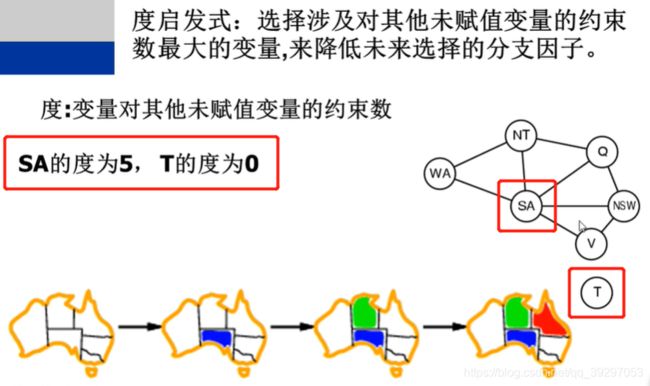
选择变量的策略二:度(degree)启发式
如图所示,着色时按照变量与其他变量之间存在的约束数量由多到少的顺序进行着色。
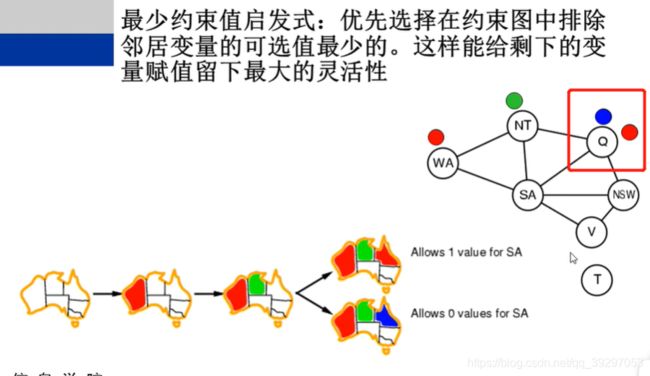
选择变量的策略三:最少约束值(Least constraining value)启发式
当进行红色方框圈起来的步骤时,有两种着色选择(蓝色和红色),我们尽量不选择之前着色没有出现过的颜色,将更多是颜色选择机会留给后面的操作,即选红色不选蓝色,因为蓝色之前没有出现过。
减少搜索空间
减少搜索空间的核心思想是在选择变量取值前就发现矛盾,减少变量值的试探,即减少搜索空间。
方法有:向前检验,约束传播,处理特殊约束,智能回溯
向前检验(Forward checking)
如图,第一步,当WA选择红色时,在与之有约束关系的NT和SA的值域中删除红色,结果见图中第二行颜色条。
第二步,当Q选择绿色时,同理,在与之有约束关系的NT,SA和NSW的值域中都删除绿色,结果如第三行颜色条所示。
以此类推,这样做的目的是减少下一次选择时的值域来达到减少搜索空间的目的。

但是,向前检查无法检测出矛盾:NT和SA相邻不同取同色,然而经过两次向前检验,NT和SA的值域里都只有蓝色。这就是矛盾所在。
解决这一矛盾的方法是约束传播,因为约束满足问题针对变量有值域和约束两方向,而向前传播只考虑的值域,没考虑约束。
约束传播(Constraint propagation):
约束传播的含义是将一个变量的约束内容传播到其他变量。
介绍约束传播之前,要先明白什么是弧相容(Arc consistency):如果对于变量X的每个值x,变量Y都有某个取值能和x保持相容(相容的意思是满足约束),则X->Y的弧是相容的。如图:

由于SA和NSW有约束关系,所以在约束传播的过程中进行弧相容检测,SA的值域只有蓝色,当SA为蓝色时,NSW可以从它的值域中选择红色来应对,所以这个弧是相容的。
如果反过来,由于NSW的值域中有蓝色,当其选择蓝色时,SA的值域没有相容的选项,所以应该再NSW中删除蓝色。如图:
这里,因为改变的NSW的值域,所以与它有关系的其他变量(Q,SA,V)都要重新进行弧相容检测。
这就是约束传播。应用弧相容能更早检测到向前检查不能发生的矛盾。可在搜索过程中每次赋值后作约束传播,保持弧相容。
三,CSP问题的局部搜索(Local search for CSPs)
局部搜索算法可以求解CSP问题(局部算法在之前的博文里有具体介绍),其中CSP问题的初始状态都要一个赋值,只不过这个赋值可能是不相容的,后续的函数一次改变一个变量取值。启发式选择最小冲突启发式,即选择会造成和其他变量的冲突最小的值。

如图所示,以最小冲突为启发式的局部搜索在n皇后问题上相比简单的回溯操作,空间复杂度有巨大的降低(40000K->4K)
