大家好呀,我是小张,最近整理资料发现归并排序的思想不仅仅只可以运用到排序中,在于一些其他场景也具有奇效,小张想通过三篇文章来给大家了解这几种场景并掌握它,接下来小张先带大家回顾一下归并排序到底是一个什么东东。
说起归并排序,它的思想就是将数据不断切半,然后将切半的数据合并为一个有序过程。
归并
归并归并,那么这个归并到底指的是什么?
假定现在给你一个两部分有序的数组(如下图),要求将两部分有序的数组合并成另一个有序数组。
我们可以很容易的想到我们初始化一个和该数组大小一致的辅助数组,设置左中右三个指针,通过左指针和mid+1指针当前的数进行比较,较小的放入辅助数组中指针后移一位。那么循环的终止条件就是left指针超过mid指针或mid+1指针超过right指针。循环此过程,我们会发现肯定有一半数据会先进入辅助数组,实例的数据,右边的数据将会进入辅助数组,循环终止。
那还有一半数据怎么办?我们可以通过left是否小于等于mid或者mid+1指针是否小于等于right来判断数据是否完全进入辅助数据,如果发生我们只需要将数据全部添加到辅助数据即可。
代码实现
public void merge(int[] data, int l, int mid, int r) {
int[] help = new int[r - l + 1];
int index1 = l;
int index2 = mid + 1;
int i = 0;
while (index1 <= mid && index2 <= r) {
help[i++] = data[index1] <= data[index2] ? data[index1++] : data[index2++];
}
// 右边越界
while (index1 <= mid) {
help[i++] = data[index1++];
}
// 左边越界
while (index2 <= r) {
help[i++] = data[index2++];
}
for (int j = 0; j < help.length; j++) {
data[l + j] = help[j];
}
}切分
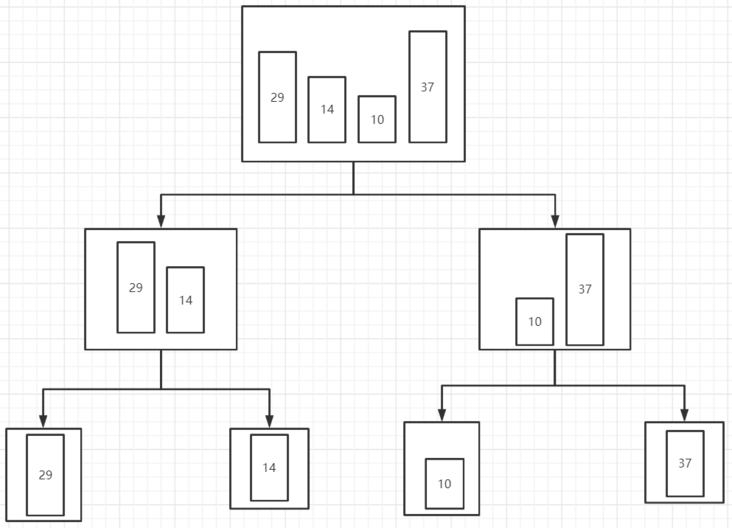
现在我们有了一个基础函数merge,那么我们是否可以将数据切分并将切分后的两个有序数组归并在一起呢?
按照上图,如果我们可以将数据拆分到不能拆分(只剩一个元素),然后再进行合并,是不是就可以起到排序的作用?
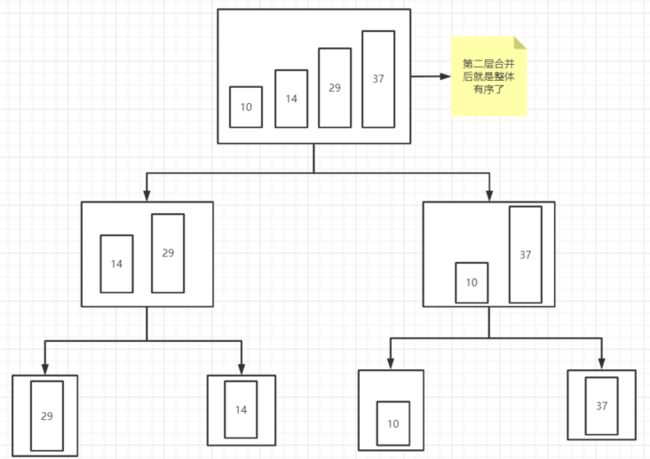
我们会发现最后一层merge之后产生的数组就是有序的数组了,回到第二层就是有序的结果了,下面展示第二层合并的过程。
相信通过图片,大家应该可以明白数据切分然后归并的过程了,其实这里就体现了归并排序的所有思想,接下来将通过代码去实现这个过程。
代码实现
熟悉递归的小伙伴会发现这就是一棵典型的递归树,那么我们就可以通过递归将数据不断的切半,然后再进行合并。
public void sort(int[] data) {
sort(data, 0, data.length - 1);
}
private void sort(int[] data, int left, int right) {
// base code 当left=right代表已经无法切分
if (left == right) {
return;
}
int mid = (left + right) / 2;
sort(data, left, mid);
sort(data, mid + 1, right);
merge(data, left, mid, right);
}递归函数的退出条件就是,当left==right意味着只剩一个元素,就不能往下继续递归了。
写在最后
归并排序的这种分治的思想在平时的处理问题上是经常出现的一种思想,将一个问题的规模不断减小,利用小规模的计算结果不断去推出大规模的结果,这种思想非常值得我们借鉴。
在下一篇,小张将给大家带来一个能够使用归并排序的场景,将一个时间复杂度为O(n^2)算法优化为O(n*logn)的过程。