数据结构 - 堆
目录
堆的分类
1、大根堆
2、小根堆
堆的实现
1、向下调整法
2、向上调整法
3、从堆中删除一个数据
堆排序
堆 (一种二叉树（完全二叉树）)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。
二叉树相关的知识见
二叉树需要掌握的基本知识_TangguTae的博客-CSDN博客
https://blog.csdn.net/weixin_43164548/article/details/123141346?spm=1001.2014.3001.5501堆的物理结构是一个数组，逻辑结构是一个完全二叉树。
堆的分类
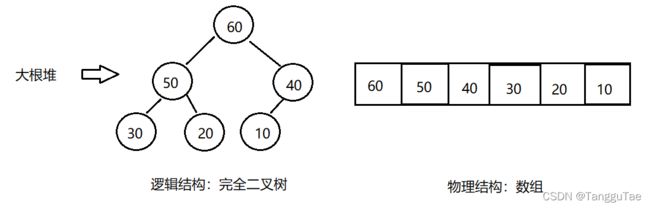
1、大根堆
堆中所有父亲节点的数值大于等于孩子节点的数值。
上述例子是一个有序的情况，把50和40交换位置也是一个大根堆。
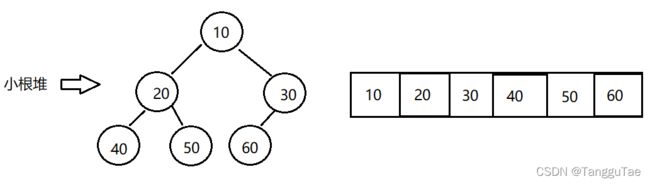
2、小根堆
堆的实现
先给出一个结论：
假设父亲节点的下标为parent
则左孩子的下标LeftChild = parent*2 + 1；右孩子的下标RightChild = parent*2 + 2。
所以可以得到parent = (child - 1)/2，child既可以是左孩子，也可以是右孩子。
在建堆之前首先得知道向下调整法来调整堆。
1、向下调整法
假设存在前提：根节点的左子树和右子树都是堆。
步骤：（小堆）
- 选出父亲节点左右孩子中较小的那一个。
- 将这个孩子与父亲节点比较，如果孩子小于父亲，则交换两者的位置，否则退出流程。
- 现在将交换前的父亲节点仍视为父亲节点，返回第一步。
- 如果父亲节点到达叶子结点的位置，结束流程。
若要想得到大堆，改变判断条件即可。
复杂度分析：因为只需要比较二叉树的高度次，所以复杂度为
void swap(int* arr1,int *arr2)//交换数组中的两个元素
{
int tmp = *arr1;
*arr1 = *arr2;
*arr2 = tmp;
}
void AdjustDown(int* arr, int len, int parent)
{
assert(arr);
while (parent * 2 + 1 < len)
{
int minChild = parent * 2 + 1;
if (parent * 2 + 2 < len)//当右子树存在时，判断左右两个节点谁的值跟小
{
minChild = (arr[parent * 2 + 1] > arr[parent * 2 + 2]) ? (parent * 2 + 2) : (parent * 2 + 1);
}
if (arr[parent] > arr[minChild])//如果父亲节点的值大于较小的孩子节点，则交换位置
{
swap(arr + parent, arr + minChild);
parent = minChild;//更新父亲节点的位置
}
else
break;
}
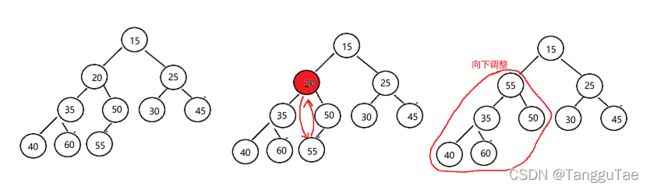
}如果前提不满足怎么办？
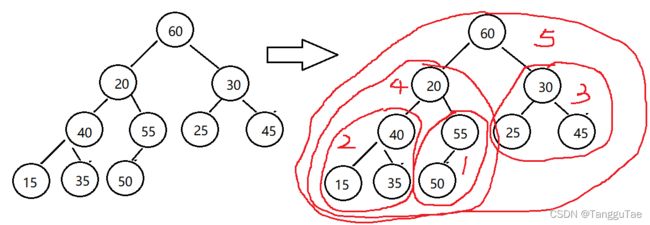
此时我们考虑从下往上，逐步调整，利用向下调整的方法，采用从倒数第一个非叶子结点开始向下调整。
//最后一个非叶子结点praent = (len-1)/2
for (int i = (sizeof(arr) / sizeof(arr[0]) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sizeof(arr) / sizeof(arr[0]), i);
}测试一下代码
int main(void)
{
int arr[] = { 60,20,30,40,55,25,45,15,35,50 };
for (int i = (sizeof(arr) / sizeof(arr[0]) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sizeof(arr) / sizeof(arr[0]), i);
}
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}
最终把一个不是堆的数组变成了堆
这个过程就叫做建堆
复杂度分析：
不失一般性，采用满二叉树代替完全二叉树，假设高度为h，总的节点数为n
从第h-1层的节点开始向下调整，这一层的每一个节点只需要一次运算，复杂度为^(−)*1
第h-2层的节点向下调整，这一层每一个节点需要两次运算，复杂度为^(−)*2
第h-3层的节点向下调整，这一层每一个节点需要三次运算，复杂度为^(−)*3
以此类推
总的计算量
，为第i层的节点数量
展开得到()=∗(−)+∗(−)+^∗(−)+…+^(−)∗
∗()= ∗(−)+ ^2∗(−)+…+^(−)∗+^(−)∗
错位相减得到()=^−−=−()
所以复杂度就为O(N)
2、向上调整法
如果在原来堆的基础上从末尾增加一个元素，如何将新的二叉树变成堆？
首先并不采用重新建堆的方法，具有一定的复杂度。此时引入一个方法叫做向上调整法
只需要新的节点与父亲节点比较，逐步向上走，就可以更新堆。
void AdjustUp(int* arr, int len)
{
//len数组的长度
int bot = len - 1;
while ((bot - 1) / 2 >= 0)//判断父亲节点是否存在
{
if (arr[bot] < arr[(bot - 1) / 2])//小堆
{
swap(arr + bot, arr + (bot - 1) / 2);
bot = (bot - 1) / 2;
}
else
break;
}
}3、从堆中删除一个数据
由于堆的物理结构是数组，如果删除数组中任意位置的元素，还需要对数组进行挪动，复杂度为O(N)，然后在新的数组基础上重新建堆，又需要O(N)的复杂度。所以这种做法是非常复杂的。
所以从堆中删除一个数据可以这样做：每次把要删除的元素与堆中最后一个元素进行交换位置，每次只删除最后的一个元素，然后对要删除元素的位置进行一次向下调整，将其重新调整为堆。
代码实现起来很简单
//HP是堆的数据结构
void DeleteData(HP* p, int locate)//删除数据
{
assert(p&&(locate>0 || locate<(p->size - 1)));//防止出错
ExchangeData(p->arr + locate - 1, p->arr + (p->size - 1));//将需要删除的元素放在尾部
(p->size)--;
AdjustDownMAX(p->arr, p->size, locate - 1);//向下调整
}堆排序
以升序的方式排序
- 先将数组变成一个大根堆
- 该堆的根节点即为数组中最大的值
- 将最大的节点与最后一个叶子节点即数组中最后的元素进行交换，并将最后一个节点在逻辑上删除
- 此时根节点的左右子树仍为堆，所以可以采用向下调整法，将新的二叉树最大的值调整到根节点，变成一个新的堆。
- 重复上述步骤，直到排序结束
复杂度分析：Nlog(N)
//堆排
void HeapSort(int* arr, int len)
{
int end = len - 1;
while (end)
{
swap(arr, arr + end);//首先将最大值换到最后
AdjustDown(arr, end, 0);//对剩下的元素进行向下调整
end--;//逻辑上删除
}
}
int main(void)
{
int arr[] = { 60,20,30,40,55,25,45,15,35,50 };
//建大堆
for (int i = (sizeof(arr) / sizeof(arr[0]) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sizeof(arr) / sizeof(arr[0]), i);
}
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}