【时间序列预测算法】——灰色预测算法介绍及代码实现
基本概念
白色系统:系统结构和参数完全已知
黑色系统:系统结构和参数完全不知,只能观测外界交互
灰色系统:系统结构和参数部分已知。适合处理贫信息系统,小样本预测问题。
灰色生成:f(原始TSD)->y,如累加生成、累减生成。可以看出灰量递增/递减过程的发展态势,使原始数据中蕴含的积分规律显化。对生成数建立起微分方程形式的模型,便于对其变化过程进行研究和描述。G 表示 Grey(灰色),M 表示 Model(模型),所以GM(m,n)表示灰色模型。
a:发展系数;b:灰作用量
GM(1,1)或GM11,11是单序列输入输出的意思。
问题举例
原始数据: [1, 2, 3, 4]
以累加生成方式为例,生成数据: [1, 1+2=3, 1+2+3=6, 1+2+3+4=10]
以累减生成方式为例,生成数据: [1, 2-1=1,3-2-1=0,4-3-2-1=-2]
以加权邻值生成方式为例,生成数据: [...]
加权邻值生成公式(通常α=0.5,此时也为移动平均(区别于ARIMA算法中的MA,就是沿着窗口长度=2滑动求窗口内的均值)):
x k ( 2 ) = α x k ( 1 ) + ( 1 − α ) x k − 1 ( 1 ) , k > 1 ; x k ( 2 ) = x k ( 1 ) , k = 1. x^{(2)}_k=αx^{(1)}_k+(1−α)x^{(1)}_{k−1},k>1;\\ x^{(2)}_k=x^{(1)}_k,k=1. xk(2)=αxk(1)+(1−α)xk−1(1),k>1;xk(2)=xk(1),k=1.
上标表示第几个序列,是序列ID
下标表示第几个元素,是元素ID
算法推导
模型:
x k ′ ( 2 ) = x k ( 2 ) − x k − 1 ( 2 ) x'^{(2)}_k=x^{(2)}_k-x^{(2)}_{k-1} xk′(2)=xk(2)−xk−1(2) 灰微分(一阶差分)算子
模型用灰微分方程表示为
x k ′ ( 2 ) + a x k ( 2 ) = b x'^{(2)}_k+ax^{(2)}_k=b xk′(2)+axk(2)=b
对应的白化方程为:
x t ′ + a x t = b x'_t+ax_t=b xt′+axt=b
求解为:
x t = x k ( 2 ) = α x k ( 1 ) + ( 1 − α ) x k − 1 ( 1 ) = b / a + e a t x_t=x^{(2)}_k=αx^{(1)}_k+(1−α)x^{(1)}_{k−1}=b/a+e^{at} xt=xk(2)=αxk(1)+(1−α)xk−1(1)=b/a+eat
根据递归的方法求得最终解( α 取 0.5 ? 1.0 ? \alpha取0.5?1.0? α取0.5?1.0?):
估 计 值 x k ( 2 ) = ( x 1 ( 1 ) − b / a ) e − a ( k − 1 ) + b / a , k > 1. 估计值x^{(2)}_k=(x^{(1)}_1-b/a)e^{-a(k-1)}+b/a,k>1. 估计值xk(2)=(x1(1)−b/a)e−a(k−1)+b/a,k>1.
估 计 值 x k ( 1 ) = 估 计 值 x k ( 2 ) − 估 计 值 x k − 1 ( 2 ) = ( x 1 ( 1 ) − b / a ) e − a ( k − 1 ) ( 1 − e a ) , k > 1. 估计值x^{(1)}_k=估计值x^{(2)}_k-估计值x^{(2)}_{k-1}\\=(x^{(1)}_1-b/a)e^{-a(k-1)}(1-e^a),k>1. 估计值xk(1)=估计值xk(2)−估计值xk−1(2)=(x1(1)−b/a)e−a(k−1)(1−ea),k>1.
↓ ↓ ↓
NOTE :第二个等式中的第一个等号不知何来,第二个等号是恒成立的。
分开:
x k ′ ( 2 ) = x k ( 2 ) − x k − 1 ( 2 ) x'^{(2)}_k=x^{(2)}_k-x^{(2)}_{k-1} xk′(2)=xk(2)−xk−1(2) 灰微分(一阶差分)
U = [ a , b ] T U=[a,b]^T U=[a,b]T
D = [ x 2 ′ , . . . , x n ′ ] T D=[x'_2,...,x'_n]^T D=[x2′,...,xn′]T
B = [ − x 2 ( 2 ) 1 ; . . . ; − x n ( 2 ) 1 ; ] B=[\\-x^{(2)}_2 \ 1;\\ \ \ \ ... ;\\ -x^{(2)}_n \ 1;\\ \\] B=[−x2(2) 1; ...;−xn(2) 1;]
模型公式可表示为矩阵形式:
D = B U D=BU D=BU
则 U = ( B T B ) − 1 B T D U=(B^TB)^{-1}B^TD U=(BTB)−1BTD
可以最小二乘法估计出a b参数,代入上面最终解。
条件检验
代码实现
# 参数设定
alpha = 0.5 # 滑动窗口平均
# TSD数据集构造
# k=1,2,3,...,16
tsd = [101.02, 102.19, 106.5, 111.08, 113.28,
115.97, 118.02, 119.99, 123.23, 132.37,
135.95, 138.82, 143.18, 146.51, 151.54,
159.47]
# 原始时序数据
plt.figure(figsize=(16, 7))
plt.plot(tsd)
plt.title("Raw TSD")
plt.show()
# 累加生成方式
def add_gen(tsd):
return [np.sum(tsd[:i + 1]) for i in range(len(tsd))]
tsd_add = add_gen(tsd)
plt.figure(figsize=(16, 7))
plt.plot(tsd_add)
plt.title("Added TSD")
plt.show()
# 求解a和b参数
x1 = tsd_add
def get_x2(x1, alpha):
return [alpha * x1[i + 1] + (1 - alpha) * x1[i] for i in range(len(x1) - 1)]
x2 = get_x2(x1, alpha)
# 为匹配矩阵相乘的shape 取第一行开始的以后
B = np.concatenate([-np.array(x2).reshape(-1, 1), np.ones((len(x2), 1))], axis=-1)
# ------------------差分函数------------------
def diff(y, d):
for d_index in range(d):
y = [y[i] - y[i - 1] for i in range(1, len(y))]
return y
# 这里使用的是累加生成序列来计算灰微分,是否换成滑动窗口平均后的x2?
D = np.array(diff(tsd_add, 1)).reshape((-1, 1)) # 灰微分
# U=(BT*B)^(-1)*BT*D
# 求逆使用np.linalg.inv((np.matmul(B.T, B)))
# 尽量不使用(np.matmul(B.T, B)) ** (-1),结果不同!
U = np.matmul(np.matmul(np.linalg.inv((np.matmul(B.T, B))), B.T), D)
a = U[0][0]
b = U[1][0]
print("a:", a, "b:", b)
def GM11(init, a, b, k):
# k>1
return (init - b / a) * np.exp(-a * (k - 1)) * (1 - np.exp(a))
def GM11_x2(init, a, b, k):
# k>1
return (init - b / a) * np.exp(-a * (k - 1)) + b/a
# k=2,...,16
predict_x1 = [GM11(x1[0], a, b, k) for k in range(1+1, len(x1)+1)]
# 下面的公式是可信的,上面的公式计算predict是x2[k]-x2[k-1]的结果,但推不出来,且实测拟合效果也很差
predict_x2 = [GM11_x2(x1[0], a, b, k) for k in range(1+1, len(x1)+1)]
plt.plot(predict_x2, label='Pred')
plt.plot(tsd_add, label='True tsd_add')#预测出来的实际上是tsd_add
plt.plot(x1, label='True x1')
plt.plot(x2, label='True x2')
plt.legend(loc=1)
plt.title("GM11 Predictions")
plt.show()
# 还原解码回tsd
tsd_predict = diff(predict_x2,1)
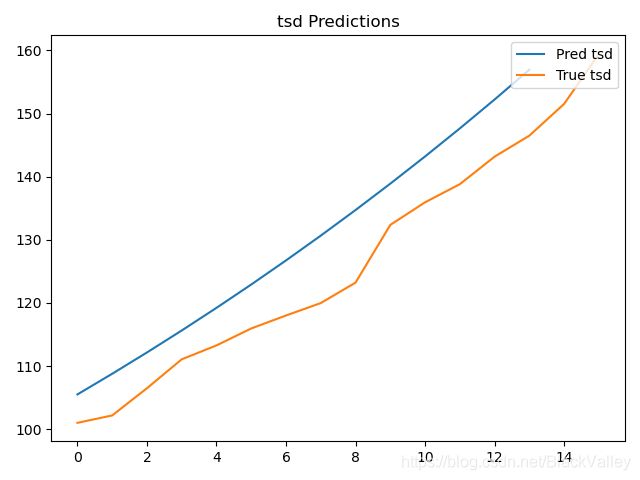
plt.plot(tsd_predict, label='Pred tsd')
plt.plot(tsd, label='True tsd')
plt.legend(loc=1)
plt.title("tsd Predictions")
plt.show()
结论
输入时间点k输出单点的预测
适合小样本
参考资料
本博客中知识点和公式参考:
博客1
知乎1
CSDN搜索
Bilibili视频1