利用python进行数据分析--时间序列(下)
与公众号同步更新,详细内容及相关ipynb文件在公众号中,公众号:AI入门小白
文章目录
-
- 时期及其算术运算
-
- 时期的频率转换
- 按季度计算的时期频率
- 将Timestamp转换为Period(及其反向过程)
- 通过数组创建PeriodIndex
- 重采样及频率转换
-
- 降采样
- OHLC重采样
- 升采样和插值
- 通过时期进⾏重采样
- 移动窗⼝函数
-
- 指数加权函数
- ⼆元移动窗⼝函数
- ⽤户定义的移动窗⼝函数
时期及其算术运算
时期(period)表示的是时间区间,⽐如数⽇、数⽉、数季、数年等。Period类所表示的就是这种数据类型,其构造函数需要⽤到⼀个字符串或整数,以及表11-4中的频率:
p = pd.Period(2007, freq='A-DEC')
p
![]()
这⾥,这个Period对象表示的是从2007年1⽉1⽇到2007年12⽉31⽇之间的整段时间。只需对Period对象加上或减去⼀个整数即可达到根据其频率进⾏位移的效果:
p + 5
p - 2

如果两个Period对象拥有相同的频率,则它们的差就是它们之间的单位数量:
pd.Period('2014', freq='A-DEC') - p
rng = pd.period_range('2000-01-01', '2000-06-30', freq='M')
rng
![]()
PeriodIndex类保存了⼀组Period,它可以在任何pandas数据结构中被⽤作轴索引:
pd.Series(np.random.randn(6), index=rng)

如果你有⼀个字符串数组,你也可以使⽤PeriodIndex类:
values = ['2001Q3', '2002Q2', '2003Q1']
index = pd.PeriodIndex(values, freq='Q-DEC')
index
![]()
时期的频率转换
Period和PeriodIndex对象都可以通过其asfreq⽅法被转换成别的频率。假设我们有⼀个年度时期,希望将其转换为当年年初或年末的⼀个⽉度时期。该任务⾮常简单:
p = pd.Period('2007', freq='A-DEC')
p
p.asfreq('M', how='start')
![]()
p.asfreq('M', how='end')
![]()
你可以将Period('2007','A-DEC')看做⼀个被划分为多个⽉度时期的时间段中的游标。图11-1对此进⾏了说明。对于⼀个不以12⽉结束的财政年度,⽉度⼦时期的归属情况就不⼀样了:
图11-1 Period频率转换示例

p = pd.Period('2007', freq='A-JUN')
p
p.asfreq('M', 'start')
p.asfreq('M', 'end')
![]()
在将⾼频率转换为低频率时,超时期(superperiod)是由⼦时期(subperiod)所属的位置决定的。例如,在A-JUN频率中,⽉份“2007年8⽉”实际上是属于周期“2008年”的:
p = pd.Period('Aug-2007', 'M')
p
![]()
p.asfreq('A-JUN')
![]()
完整的PeriodIndex或TimeSeries的频率转换⽅式也是如此:
rng = pd.period_range('2006', '2009', freq='A-DEC')
ts = pd.Series(np.random.randn(len(rng)), index=rng)
ts
ts.asfreq('M', how='start')

这⾥,根据年度时期的第⼀个⽉,每年的时期被取代为每⽉的时期。如果我们想要每年的最后⼀个⼯作⽇,我们可以使⽤“B”频率,并指明想要该时期的末尾:
ts.asfreq('B', how='end')
按季度计算的时期频率
季度型数据在会计、⾦融等领域中很常⻅。许多季度型数据都会涉及“财年末”的概念,通常是⼀年12个⽉中某⽉的最后⼀个⽇历⽇或⼯作⽇。就这⼀点来说,时期"2012Q4"根据财年末的不同会有不同的含义。pandas⽀持12种可能的季度型频率,即QJAN到Q-DEC:
p = pd.Period('2012Q4', freq='Q-JAN') # 2012Q4: 2012年第四季度
p
![]()
在以1⽉结束的财年中,2012Q4是从11⽉到1⽉(将其转换为⽇型频率就明⽩了)。图11-2对此进⾏了说明:
图11.2 不同季度型频率之间的转换

p.asfreq('D', 'start')
![]()
p.asfreq('D', 'end')
![]()
因此,Period之间的算术运算会⾮常简单。例如,要获取该季度倒数第⼆个⼯作⽇下午4点的时间戳,你可以这样:
p4pm = (p.asfreq('B', 'e') - 1).asfreq('T', 's') + 16 * 60
p4pm
p4pm.to_timestamp()
![]()
period_range可⽤于⽣成季度型范围。季度型范围的算术运算也跟上⾯是⼀样的:
rng = pd.period_range('2011Q3', '2012Q4', freq='Q-JAN')
ts = pd.Series(np.arange(len(rng)), index=rng)
ts
new_rng = (rng.asfreq('B', 'e') - 1).asfreq('T', 's') + 16 * 60
ts.index = new_rng.to_timestamp()
ts
将Timestamp转换为Period(及其反向过程)
通过使⽤to_period⽅法,可以将由时间戳索引的Series和DataFrame对象转换为以时期索引:
rng = pd.date_range('2000-01-01', periods=3, freq='M')
ts = pd.Series(np.random.randn(3), index=rng)
ts
pts = ts.to_period()
pts

由于时期指的是⾮重叠时间区间,因此对于给定的频率,⼀个时间戳只能属于⼀个时期。新PeriodIndex的频率默认是从时间戳推断⽽来的,你也可以指定任何别的频率。结果中允许存在重复时期:
rng = pd.date_range('1/29/2000', periods=6, freq='D')
ts2 = pd.Series(np.random.randn(6), index=rng)
ts2
ts2.to_period('M')
pts = ts2.to_period()
pts
pts.to_timestamp(how='end')
通过数组创建PeriodIndex
固定频率的数据集通常会将时间信息分开存放在多个列中。例如,在下⾯这个宏观经济数据集中,年度和季度就分别存放在不同的列中:
data = pd.read_csv('./macrodata.csv')
data.head(5)
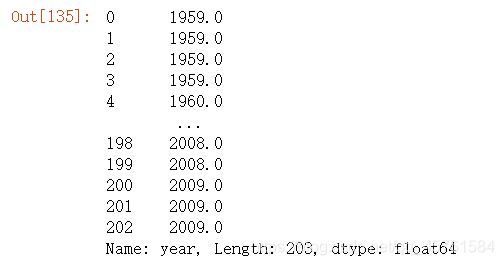
data.year
data.quarter

通过通过将这些数组以及⼀个频率传⼊PeriodIndex,就可以将它们合并成DataFrame的⼀个索引:
index = pd.PeriodIndex(year=data.year, quarter=data.quarter,
freq='Q-DEC')
index
data.index = index
data.infl
重采样及频率转换
重采样(resampling)指的是将时间序列从⼀个频率转换到另⼀个频率的处理过程。将⾼频率数据聚合到低频率称为降采样(downsampling),⽽将低频率数据转换到⾼频率则称为升采样(upsampling)。并不是所有的重采样都能被划分到这两个⼤类中。例如,将W-WED(每周三)转换为W-FRI既不是降采样也不是升采样。
pandas对象都带有⼀个resample⽅法,它是各种频率转换⼯作的主⼒函数。resample有⼀个类似于groupby的API,调⽤resample可以分组数据,然后会调⽤⼀个聚合函数:
rng = pd.date_range('2000-01-01', periods=100, freq='D')
ts = pd.Series(np.random.randn(len(rng)), index=rng)
ts
ts.resample('M').mean()
ts.resample('M', kind='period').mean()

resample是⼀个灵活⾼效的⽅法,可⽤于处理⾮常⼤的时间序列。我将通过⼀系列的示例说明其⽤法。表11-5总结它的⼀些选项。
表11-5 resample⽅法的参数
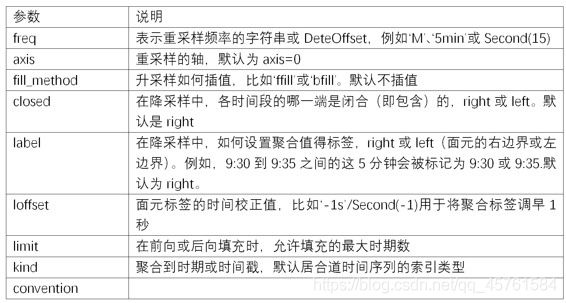
降采样
将数据聚合到规律的低频率是⼀件⾮常普通的时间序列处理任务。待聚合的数据不必拥有固定的频率,期望的频率会⾃动定义聚合的⾯元边界,这些⾯元⽤于将时间序列拆分为多个⽚段。例如,要转换到⽉度频率(‘M’或’BM’),数据需要被划分到多个单⽉时间段中。各时间段都是半开放的。⼀个数据点只能属于⼀个时间段,所有时间段的并集必须能组成整个时间帧。在⽤resample对数据进⾏降采样时,需要考虑两样东⻄:
- 各区间哪边是闭合的。
- 如何标记各个聚合⾯元,⽤区间的开头还是末尾。
为了说明,我们来看⼀些“1分钟”数据:
rng = pd.date_range('2000-01-01', periods=12, freq='T')
ts = pd.Series(np.arange(12), index=rng)
ts
ts.resample('5min', closed='right').sum()
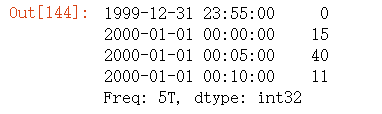
传⼊的频率将会以“5分钟”的增量定义⾯元边界。默认情况下,⾯元的右边界是包含的,因此00:00到00:05的区间中是包含00:05的。传⼊closed='left'会让区间以左边界闭合:
ts.resample('5min', closed='left').sum()
时间序列以各⾯元右边界的时间戳进⾏标记。传⼊label='right'即可⽤⾯元的邮编界对其进⾏标记:
ts.resample('5min', closed='right', label='right').sum()
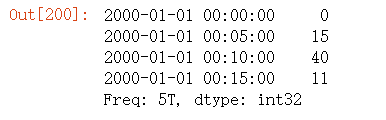
图11-3说明了“1分钟”数据被转换为“5分钟”数据的处理过程。
图11-3 各种closed、label约定的“5分钟”重采样演示
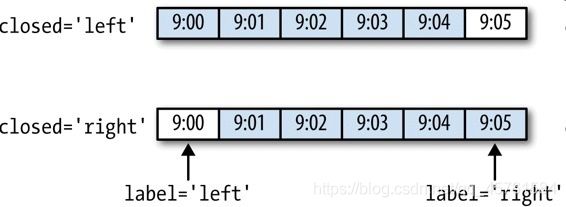
最后,你可能希望对结果索引做⼀些位移,⽐如从右边界减去⼀秒以便更容易明⽩该时间戳到底表示的是哪个区间。只需通过to_offset设置⼀个字符串或⽇期偏移量即可实现这个⽬的:
from pandas.tseries.frequencies import to_offset
df = ts.resample("5min", closed='right',
label='right').sum()
df.index = df.index + to_offset("-1s")
df.index
df

此外,也可以通过调⽤结果对象的shift⽅法来实现该⽬的,这样就不需要设置to_offset了。
OHLC重采样
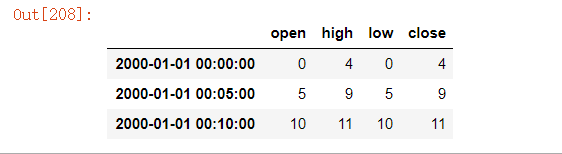
⾦融领域中有⼀种⽆所不在的时间序列聚合⽅式,即计算各⾯元的四个值:第⼀个值(open,开盘)、最后⼀个值(close,收盘)、最⼤值(high,最⾼)以及最⼩值(low,最低)。传⼊how='ohlc'即可得到⼀个含有这四种聚合值的DataFrame。整个过程很⾼效,只需⼀次扫描即可计算出结果:
ts.resample('5min').ohlc()
升采样和插值
在将数据从低频率转换到⾼频率时,就不需要聚合了。我们来看⼀个带有⼀些周型数据的DataFrame:
frame = pd.DataFrame(np.random.randn(2, 4),
index=pd.date_range('1/1/2000', periods=2,
freq='W-WED'),
columns=['Colorado', 'Texas', 'New York', 'Ohio'])
frame

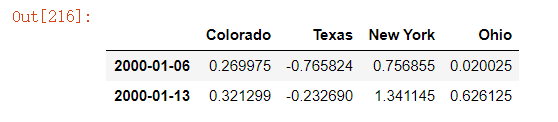
当你对这个数据进⾏聚合,每组只有⼀个值,这样就会引⼊缺失值。我们使⽤asfreq⽅法转换成⾼频,不经过聚合:
df_daily = frame.resample('D').asfreq()
df_daily

假设你想要⽤前⾯的周型值填充“⾮星期三”。resample的填充和插值⽅式跟fillna和reindex的⼀样:
frame.resample('D').ffill()
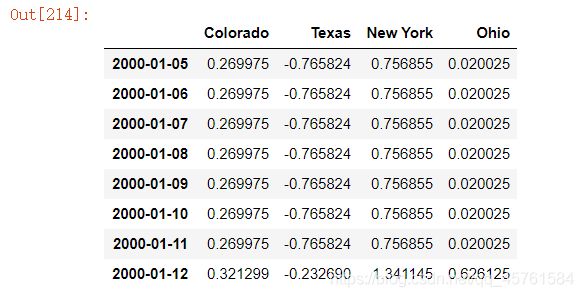
同样,这⾥也可以只填充指定的时期数(⽬的是限制前⾯的观测值的持续使⽤距离):
frame.resample('D').ffill(limit=2)
frame.resample('W-THU').ffill()
通过时期进⾏重采样
对那些使⽤时期索引的数据进⾏重采样与时间戳很像:
frame = pd.DataFrame(np.random.randn(24, 4),
index=pd.period_range('1-2000', '12-2001',
freq='M'),
columns=['Colorado', 'Texas', 'New York', 'Ohio'])
frame[:5]
annual_frame = frame.resample('A-DEC').mean()
annual_frame
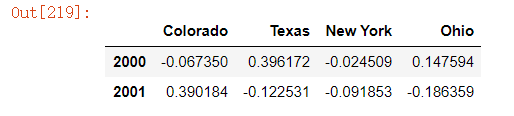
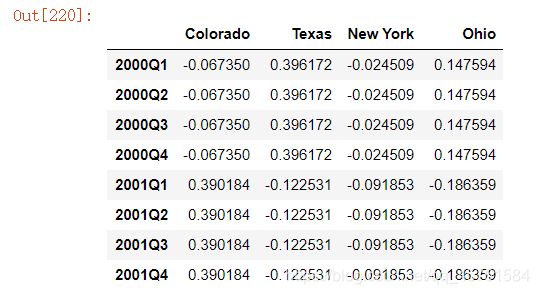
升采样要稍微麻烦⼀些,因为你必须决定在新频率中各区间的哪端⽤于放置原来的值,就像asfreq⽅法那样。convention参数默认为’start’,可设置为’end’:
# Q-DEC: 季度,年末12月
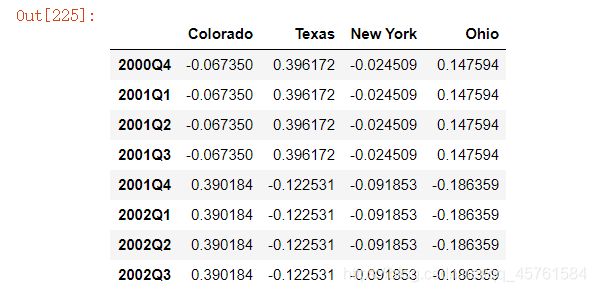
annual_frame.resample('Q-DEC').ffill()
annual_frame.resample('Q-DEC', convention='end').ffill()

由于时期指的是时间区间,所以升采样和降采样的规则就⽐较严格:
- 在降采样中,⽬标频率必须是源频率的⼦时期(subperiod)。
- 在升采样中,⽬标频率必须是源频率的超时期(superperiod)。
如果不满⾜这些条件,就会引发异常。这主要影响的是按季、 年、周计算的频率。例如,由Q-MAR定义的时间区间只能升采样为A-MAR、A-JUN、A-SEP、A-DEC等:
annual_frame.resample('Q-MAR').ffill()
移动窗⼝函数
在移动窗⼝(可以带有指数衰减权数)上计算的各种统计函数也是⼀类常⻅于时间序列的数组变换。这样可以圆滑噪⾳数据或断裂数据。我将它们称为移动窗⼝函数(moving window function),其中还包括那些窗⼝不定⻓的函数(如指数加权移动平均)。跟其他统计函数⼀样,移动窗⼝函数也会⾃动排除缺失值。
开始之前,我们加载⼀些时间序列数据,将其重采样为⼯作⽇频率:
close_px_all = pd.read_csv('./stock_px_2.csv',
parse_dates=True, index_col=0)
close_px = close_px_all[['AAPL', 'MSFT', 'XOM']]
close_px = close_px.resample('B').ffill()
close_px

现在引⼊rolling运算符,它与resample和groupby很像。可以在TimeSeries或DataFrame以及⼀个window(表示期数,⻅图11-4)上调⽤它:
plt.rcParams['font.sans-serif'] = ['simhei']
close_px.AAPL.plot()
close_px.AAPL.rolling(250).mean().plot().set_title('图11-4 苹果公司股价的250日均线')

表达式rolling(250)与groupby很像,但不是对其进⾏分组、创建⼀个按照250天分组的滑动窗⼝对象。然后,我们就得到了苹果公司股价的250天的移动窗⼝。
默认情况下,诸如rolling_mean这样的函数需要指定数量的⾮NA观测值。可以修改该⾏为以解决缺失数据的问题。其实,在时间序列开始处尚不⾜窗⼝期的那些数据就是个特例(⻅图11-5):
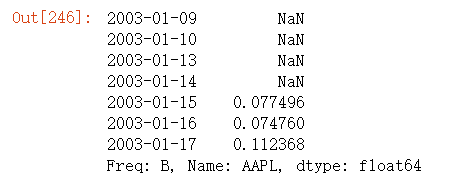
appl_std250 = close_px.AAPL.rolling(250, min_periods=10).std()
appl_std250[5:12]
appl_std250.plot().set_title('图11-5 苹果公司250日每日回报标准差')
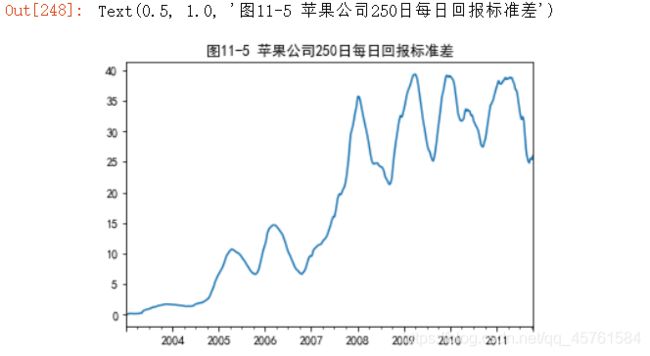
要计算扩展窗⼝平均(expanding window mean),可以使⽤expanding⽽不是rolling。“扩展”意味着,从时间序列的起始处开始窗⼝,增加窗⼝直到它超过所有的序列。apple_std250时间序列的扩展窗⼝平均如下所示:
expanding_mean = appl_std250.expanding().mean()
对DataFrame调⽤rolling_mean(以及与之类似的函数)会将转换应⽤到所有的列上(⻅图11-6):
close_px.rolling(60).mean().plot(logy=True).set_title('图11-6 各股价60日均线(对数Y轴)')
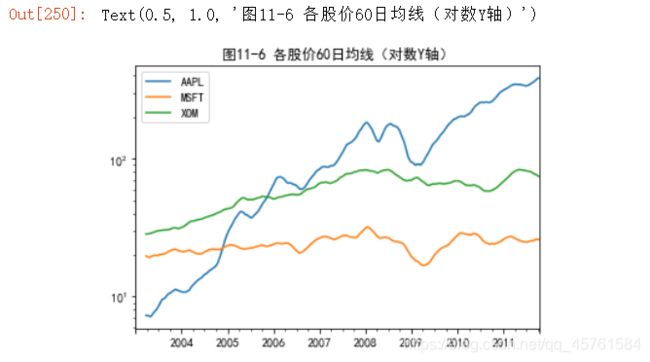
rolling函数也可以接受⼀个指定固定⼤⼩时间补偿字符串,⽽不是⼀组时期。这样可以⽅便处理不规律的时间序列。这些字符串也可以传递给resample。例如,我们可以计算20天的滚动均值,如下所示:
close_px.rolling('20D').mean()
指数加权函数
另⼀种使⽤固定⼤⼩窗⼝及相等权数观测值的办法是,定义⼀个衰减因⼦(decay factor)常量,以便使近期的观测值拥有更⼤的权数。衰减因⼦的定义⽅式有很多,⽐较流⾏的是使⽤时间间隔(span),它可以使结果兼容于窗⼝⼤⼩等于时间间隔的简单移动窗⼝(simple moving window)函数。
由于指数加权统计会赋予近期的观测值更⼤的权数,因此相对于等权统计,它能“适应”更快的变化。
除了rolling和expanding,pandas还有ewm运算符。下⾯这个例⼦对⽐了苹果公司股价的60⽇移动平均和span=60的指数加权移动平均(如图11-7所示):
aapl_px = close_px.AAPL['2006':'2007']
ma60 = aapl_px.rolling(30, min_periods=20).mean()
ewma60 = aapl_px.ewm(span=30).mean()
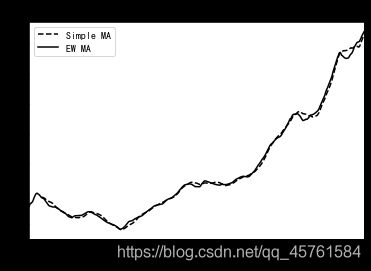
ma60.plot(style='k--', label='Simple MA')
ewma60.plot(style='k-', label='EW MA').set_title('图11-7 简单移动平均与指数加权移动平均')
plt.legend()
⼆元移动窗⼝函数
有些统计运算(如相关系数和协⽅差)需要在两个时间序列上执⾏。例如,⾦融分析师常常对某只股票对某个参考指数(如标准普尔500指数)的相关系数感兴趣。要进⾏说明,我们先计算我们感兴趣的时间序列的百分数变化:
spx_px = close_px_all['SPX']
spx_rets = spx_px.pct_change()
returns = close_px.pct_change()
调⽤rolling之后,corr聚合函数开始计算与spx_rets滚动相关系数(结果⻅图11-8):
corr = returns.AAPL.rolling(125, min_periods=100).corr(spx_rets)
corr.plot().set_title('图11-8 AAPL 6个月的回报与标准普尔500指数的相关系数')
假设你想要⼀次性计算多只股票与标准普尔500指数的相关系数。虽然编写⼀个循环并新建⼀个DataFrame不是什么难事,但⽐较啰嗦。其实,只需传⼊⼀个TimeSeries和⼀个DataFrame,rolling_corr就会⾃动计算TimeSeries(本例中就是spx_rets)与DataFrame各列的相关系数。结果如图11-9所示:
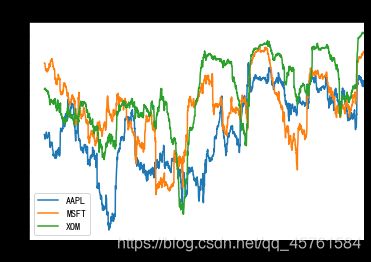
corr = returns.rolling(125, min_periods=100).corr(spx_rets)
corr.plot().set_title('图11-9 3只股票6个月的回报与标准普尔500指数的相关系数')
⽤户定义的移动窗⼝函数
rolling_apply函数使你能够在移动窗⼝上应⽤⾃⼰设计的数组函数。唯⼀要求的就是:该函数要能从数组的各个⽚段中产⽣单个值(即约简)。⽐如说,当我们⽤rolling(...).quantile(q)计算样本分位数时,可能对样本中特定值的百分等级感兴趣。
scipy.stats.percentileofscore函数就能达到这个⽬的(结果⻅图11-10):
from scipy.stats import percentileofscore
score_at_2percent = lambda x: percentileofscore(x, 0.02)
result = returns.AAPL.rolling(250).apply(score_at_2percent)
result.plot().set_title('图11-10 AAPL 2%回报率的百分等级(一年窗口期)')