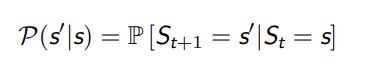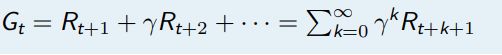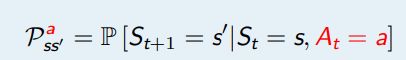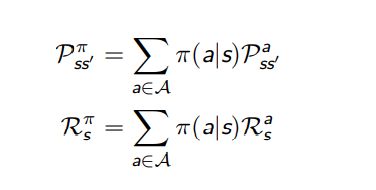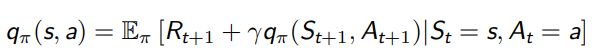马尔可夫决策过程-强化学习学习笔记(二)

概念引入

强化学习的通俗理解

马尔可夫的通俗介绍

简介

马尔可夫决策过程 (Markov Decision Processes, MDPs)是对强化学习问题的数学描述.

马尔可夫决策过程（Markov Decision Process, MDP）是序贯决策（sequential decision）的数学模型，用于在系统状态具有马尔可夫性质的环境中模拟智能体可实现的随机性策略与回报 。MDP的得名来自于俄国数学家安德雷·马尔可夫（Андрей Андреевич Марков），以纪念其为马尔可夫链所做的研究 。
MDP基于一组交互对象，即智能体和环境进行构建，所具有的要素包括状态、动作、策略和奖励 。在MDP的模拟中，智能体会感知当前的系统状态，按策略对环境实施动作，从而改变环境的状态并得到奖励，奖励随时间的积累被称为回报 。
MDP的理论基础是马尔可夫链，因此也被视为考虑了动作的马尔可夫模型 。在离散时间上建立的MDP被称为“离散时间马尔可夫决策过程（descrete-time MDP）”，反之则被称为“连续时间马尔可夫决策过程（continuous-time MDP）”。此外MDP存在一些变体，包括部分可观察马尔可夫决策过程、约束马尔可夫决策过程和模糊马尔可夫决策过程。
在应用方面，MDP被用于机器学习中强化学习（reinforcement learning）问题的建模 。通过使用动态规划、随机采样等方法，MDP可以求解使回报最大化的智能体策略 ，并在自动控制、推荐系统等主题中得到应用

• 要求环境是全观测的.
• 几乎所有的 RL 问题都能用 MDPs 来描述
• 最优控制问题可以描述成连续 MDPs
• 部分观测环境可以转化成 POMDPs
• 赌博机问题是只有一个状态的 MDPs

符号说明

用大写字母表示随机变量：S, A, R 等
用小写字母表示某一个具体的值：s, a,r 等
用空心字母表示统计运算符：E, P 等
用花体字母表示集合或函数：S, A,P 等

马尔可夫性

马氏性(Markov Property)用来描述一种特殊的、定义在某状态空间S上的随机变量列 {X(n): n>=0} 的性质，满足 P( X(n) = i(n) | X(n-1) = i(n-1), … , X(0) = i(0) ) = P( X(n) = i(n) | X(n-1) = i(n-1) )，可以理解为已知当前状态为i(n-1)的情况下，下一步状态为i(n)的概率只与i(n-1)有关，与之前的状态无关。马氏性有一个等价命题可以帮助理解：已知当前状态情况下，过去事件与未来相互独立。

简单来说
如果在 t 时刻的状态 St 满足如下等式，那么这个状态被称为马尔可夫状态，或者说该状态满足马尔可夫性.

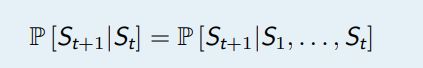
状态 St 包含了所有历史相关信息，或者说历史的所有状态的相关信息都在当前状态 St 上体现出来
，一旦 St 知道了，那么 S1, S2, . . . , St−1 都可以被抛弃，数学上可以认为：状态是将来的充分统计量
因此，这里要求环境全观测

状态转移矩阵

状态转移矩阵是俄国数学家马尔科夫提出的控制理论中的矩阵，是时间和初始时间的函数，可以将时间的状态向量和此矩阵相乘，得到时间时的状态向量。他在20世纪初发现：一个系统的某些因素在转移过程中，第n次结果只受第n-1的结果影响，即只与上一时刻所处状态有关，而与过去状态无关。 在马尔科夫分析中，引入状态转移这个概念。所谓状态是指客观事物可能出现或存在的状态；状态转移是指客观事物由一种状态转移到另一种状态。

状态转移概率指从一个马尔可夫状态s 跳转到后继状态 (successorstate)s′ 的概率

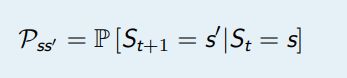
所有的状态组成行，所有的后继状态组成列，我们得到状态转移矩阵

• n 表示状态的个数
• 由于 P 代表了整个状态转移的集合，所以用花体
• 每行元素相加等于 1

用函数表达，就是

状态数量太多或者是无穷大（连续状态）时，更适合使用状态转移函数，此时

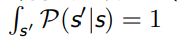
马尔可夫过程

马尔可夫过程（Markov process）是一类随机过程。它的原始模型马尔可夫链，由俄国数学家A.A.马尔可夫于1907年提出。马尔可夫过程是研究离散事件动态系统状态空间的重要方法，它的数学基础是随机过程理论
一个马尔可夫过程 (Markov process, MP ) 是一个无记忆的随机过程，即一些马尔可夫状态的序列
马尔可夫过程可以由一个二元组来定义 ⟨S,P⟩，S 代表了状态的集合，P 描述了状态转移矩阵。

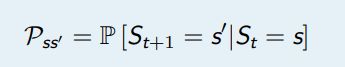
片段

强化学习中，从初始状态 S1 到终止状态的序列过程，被称为一个片段

• 如果一个任务总以终止状态结束，那么这个任务被称为片段任务(episodic task)
• 如果一个任务会没有终止状态，会被无限执行下去，这被称为连续性任务 (continuing task)

马尔可夫奖励过程

马尔可夫过程主要描述的是状态之间的转移关系，在这个转移关系上，赋予不同的奖励值即得到了马尔可夫奖励过程。

马尔可夫奖励 (Markov Reward Process, MRP) 过程由一个四元组组成⟨S,P, R, γ⟩

• S 代表了状态的集合
• P 描述了状态转移矩阵

• R 表示奖励函数，R(s) 描述了在状态 s 的奖励，
• R(s) = E [Rt+1|St = s]
• γ 表示衰减因子，γ ∈ [0, 1]

回报值

• 奖励值：对每一个状态的评价
• 回报值: 对每一个片段的评价

回报值 (return Gt) 是从时间 t 处开始的累计衰减奖励

• 对于片段性任务:
  

• 对于连续性任务

这个时候，我们结合前面所学，把旧概念做一定的挖掘

对于片段

终止状态等价于自身转移概率为 1，奖励为 0 的的状态，因此我们能够将片段性任务和连续性任务统一表达。

这里当 T = ∞ 时，表示连续性任务，否则即为片段性任务

然后是衰减值

用指数来表达衰减值的原因

• 影响未来的因素不仅仅包含当前，我们对未来的把握也是逐渐衰减的，一般情况下，我们更关注短时间的反馈
• 一个参数就描述了整个衰减过程，只需要调节这一个参数 γ 即可以调节长时奖励和短时奖励的权衡 (trade-off)，指数衰减形式又很容易进行数学分析，指数衰减是对回报值的有界保证，避免了循环 MRP 和连续性 MRP，情况下回报值变成无穷大

值函数

• 回报值是一次片段的结果，存在很大的样本偏差
• 回报值的角标是 t，值函数关注的是状态 s

一个 MRP 的值函数如下定义

这里的值函数针对的是状态 s，所以称为状态值函数，又称 V 函数
Gt 是一个随机变量
这里使用小写的 v 函数，代表了真实存在的值函数

MRPs 中的贝尔曼方程

贝尔曼方程（Bellman Equation）也被称作动态规划方程（Dynamic Programming Equation），由理查·贝尔曼（Richard Bellman）发现。贝尔曼方程是动态规划（Dynamic Programming）这些数学最佳化方法能够达到最佳化的必要条件。此方程把“决策问题在特定时间怎么的值”以“来自初始选择的报酬比从初始选择衍生的决策问题的值”的形式表示。借此这个方式把动态最佳化问题变成简单的子问题，而这些子问题遵守从贝尔曼所提出来的“最佳化还原理”。

贝尔曼方程是关于未知函数（目标函数）的函数方程组。应用最优化原理和嵌入原理建立函数方程组的方法称为函数方程法。在实际运用中要按照具体问题寻求特殊解法。动态规划理论开拓了函数方程理论中许多新的领域。
特点和应用范围 ：
若多阶段决策过程为连续型，则动态规划与变分法处理的问题有共同之处。动态规划原理可用来将变分法问题归结为多阶段决策过程，用动态规划的贝尔曼方程求解。在最优控制理论中动态规划方法比极大值原理更为适用 [1] ，但动态规划还缺少严格的逻辑基础。
60年代，В．Г．沃尔昌斯基对动态规划方法作了数学论证。
动态规划方法的五个特点：
①在策略变量较多时，与策略穷举法相比可降低维数；
②在给定的定义域或限制条件下很难用微分方法求极值的函数，可用动态规划方法求极值；
③对于不能用解析形式表达的函数,可给出递推关系求数值解;
④动态规划方法可以解决古典方法不能处理的问题，如两点边值问题和隐变分问题等；
⑤许多数学规划问题均可用动态规划方法来解决，例如，含有随时间或空间变化的因素的经济问题。
投资问题、库存问题、生产计划、资源分配、设备更新、最优搜索、马尔可夫决策过程，以及最优控制和自适应控制等问题，均可用动态规划方法来处理。

值函数的表达式可以分解成两部分

• 瞬时奖励 Rt+1
• 后继状态 St+1 的值函数乘上一个衰减系数

• 体现了 v(s) 与 v(St+1) 之间的迭代关系
• 注意 s 小写，St+1 大写

如果我们已知转移矩阵 P，那么

当 γ = 1 时 0.6 = −2 + 0.6 × 10 + 0.4 × −8.5

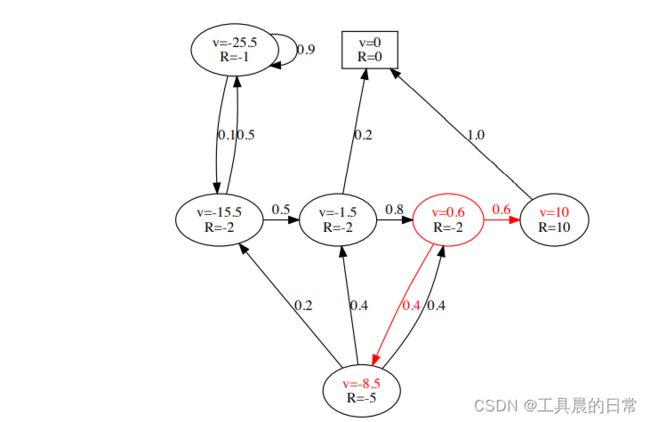
贝尔曼方程的矩阵形式

使用矩阵-向量的形式表达贝尔曼方程，即

假设状态集合为 S = {s1,s2, . . . ,sn}，那么

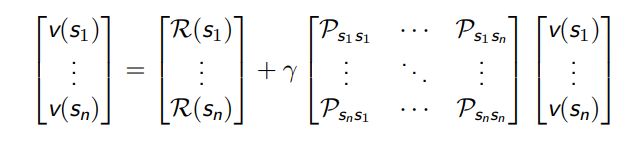
贝尔曼方程本质上是一个线性方程，可以直接解

计算复杂度

要求已知状态转移矩阵 P
直接求解的方式仅限于小的 MRPs

与 MP 和 MRP 的区别

MP 和 MRP 中，我们都是作为观察者，去观察其中的状态转移现
象，去计算回报值

• 对于一个 RL 问题，我们更希望去改变状态转移的流程，去最大化回报值

• 通过在 MRP 中引入决策即得到了马尔可夫决策过程（MarkovDecision Processes, MDPs）

• 通过在 MRP 中引入决策即得到了马尔可夫决策过程（Markov
  Decision Processes, MDPs）

马尔可夫决策过程

马尔可夫决策过程（Markov Decision Process, MDP）是序贯决策（sequential decision）的数学模型，用于在系统状态具有马尔可夫性质的环境中模拟智能体可实现的随机性策略与回报 [。MDP的得名来自于俄国数学家安德雷·马尔可夫（Андрей Андреевич Марков），以纪念其为马尔可夫链所做的研究 [3] 。
MDP基于一组交互对象，即智能体和环境进行构建，所具有的要素包括状态、动作、策略和奖励 。在MDP的模拟中，智能体会感知当前的系统状态，按策略对环境实施动作，从而改变环境的状态并得到奖励，奖励随时间的积累被称为回报 。
MDP的理论基础是马尔可夫链，因此也被视为考虑了动作的马尔可夫模型 。在离散时间上建立的MDP被称为“离散时间马尔可夫决策过程（descrete-time MDP）”，反之则被称为“连续时间马尔可夫决策过程（continuous-time MDP）” 。此外MDP存在一些变体，包括部分可观察马尔可夫决策过程、约束马尔可夫决策过程和模糊马尔可夫决策过程。
在应用方面，MDP被用于机器学习中强化学习（reinforcement learning）问题的建模 。通过使用动态规划、随机采样等方法，MDP可以求解使回报最大化的智能体策略 ，并在自动控制、推荐系统等主题中得到应用 。

一个马尔可夫决策过程 (MDPs) 由一个五元组构成 ⟨S, A,P, R, γ⟩

• S 代表了状态的集合

• A 代表了动作的集合

• P 描述了状态转移矩阵
  

• R 表示奖励函数，R(s, a) 描述了在状态 s做动作 a的奖励，
  
  γ 表示衰减因子，γ ∈ [0, 1]

策略

我们将之前 MRPs 中的状态转移矩阵分成了两个部分

• 能被智能体控制的策略, Policy
• MDPs 中的转移矩阵P (不受智能体控制，认为是环境的一部分)

在 MDPs 中，一个策略 (Policy)π是在给定状态下的动作的概率分布

• 策略是对智能体行为的全部描述
• MDPs 中的策略是基于马尔可夫状态的（而不是基于历史）
• 策略是时间稳定的，只与 s 有关，与时间 t 无关
• 策略是 RL 问题的终极目标
• 如果策略的概率分布输出都是独热的 (one-hot)2的，那么称为确定性策略，否则即为随机策略

MDPs 和 MRPs 之间的关系

对于一个 MDP 问题 ⟨S, A,P, R, γ⟩, 如果给定了策略 π
MDP 将会退化成

此时

MDPs 中的值函数

在 MDPs 问题中，由于动作的引入，值函数分为了两种：1，状态值函数（V 函数）2，状态动作值函数 (Q 函数)

MDPs 中的状态值函数是从状态 s 开始，使用策略 π 得到的期望回报值

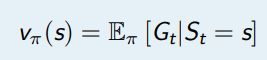
MDPs 中的状态动作值函数是从状态 s 开始，执行动作 a，然后使用策略 π 得到的期望回报值

和 MRP 相似，MDPs 中的值函数也能分解成瞬时奖励和后继状态的值函数两部分

V 函数与 Q 函数之间的相互转化

贝尔曼期望方程-V 函数

实际上等价于

贝尔曼期望方程-Q 函数

实际上等价于

贝尔曼期望方程的矩阵形式

MDPs 下的贝尔曼期望方程和 MRP 的形式相同。

同样地，可以直接求解

求解的要求

• 已知 π(a|s)
• 已知

最优值函数

之前值函数，以及贝尔曼期望方程针对的都是给定策略 π 的情况，是一个评价的问题。现在我们来考虑强化学习中的优化问题，即找出最好的策略。
最优值函数指的是在所有策略中的值函数最大值，其中包括最优 V 函数和最优 Q 函数

最优值函数指的是一个 MDP 中所能达到的最佳性能，如果我们找到最优值函数即相当于这个 MDP 已经解决了

最优策略

为了比较不同策略的好坏，我们要定义策略的比较关系

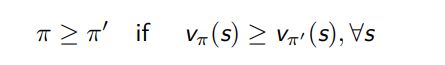
对于任何 MDPs 问题，
总存在一个策略 π∗ 要好于或等于其他所有的策略，π∗ ≥ π, ∀π
所有的最优策略都能够实现最优的 V 函数 vπ∗(s) = v∗(s)
所有的最优策略都能够实现最优的 Q 函数 qπ∗(s, a) = q∗(s, a)

**当我们已知了最优 Q 函数后，我们能够马上求出最优策略，只要根据q∗(s, a) 选择相应的动作即可。
**

由此可以得出，对于任何 MDPs 问题，总存在一个确定性的最优策略

v∗ 与 q∗ 的相互转化

之前我们已经探讨了 vπ(s) 和 qπ(s, a) 之间的关系——贝尔曼期望方程，同样地，v∗(s) 和 q∗(s, a) 也存在递归的关系——贝尔曼最优方程

和贝尔曼期望方程的关系

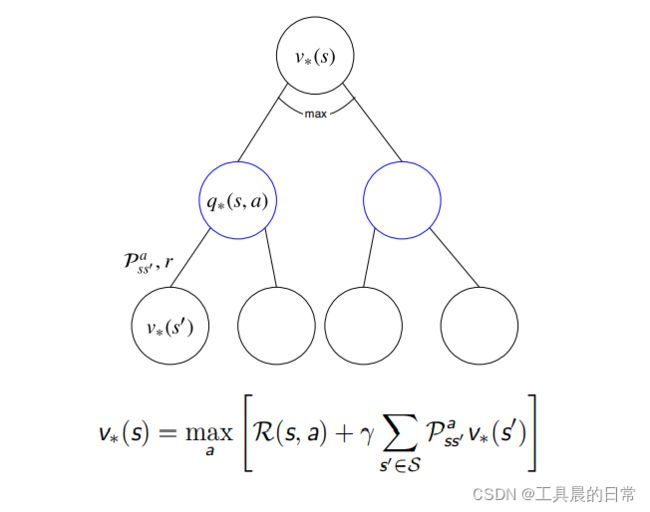
贝尔曼最优方程——V 函数

贝尔曼最优方程——Q 函数

和贝尔曼期望方程的关系

贝尔曼最优方程本质上就是利用了 π∗ 的特点，将求期望的算子转
化成了 maxa，在贝尔曼期望方程中，π 是已知的。而在贝尔曼最优方程中，π∗是未知的解贝尔曼期望方程的过程即对应了评价，解贝尔曼最优方程的过程即对应了优化。