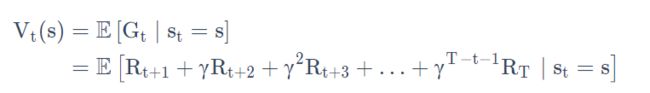强化学习笔记【2】马尔可夫决策过程（MDP）

该系列主要是听李宏毅老师的《深度强化学习》过程中记下的一些听课心得，除了李宏毅老师的强化学习课程之外，为保证内容的完整性，我还参考了一些其他的课程，包括周博磊老师的《强化学习纲要》、李科浇老师的《百度强化学习》以及多个强化学习的经典资料作为补充。

使用说明

• 笔记【4】到笔记【11】为李宏毅《深度强化学习》的部分；
• 笔记 【1】和笔记 【2】根据《强化学习纲要》整理而来；
• 笔记 【3】 和笔记 【12】根据《百度强化学习》 整理而来。

一、马尔可夫过程(Markov Process，MP)

(1) 马尔可夫性质

马尔可夫性质意味着未来只取决于现在，而与过去无关。马尔可夫性质是所有马尔可夫过程的基础。

因此，状态符合马尔可夫代表：当前状态的下一个状态只与当前状态有关，而与当前状态之前的状态无关。这是我们对于强化学习中状态的假设。

我们设状态的历史ht={s1,s2,s3,…,st}，那么：

P(St+1|St)= P(St+1|ht)

P(St+1|St,at)= P(St+1|ht,at)

(2) 马尔可夫链(Markov Chain)

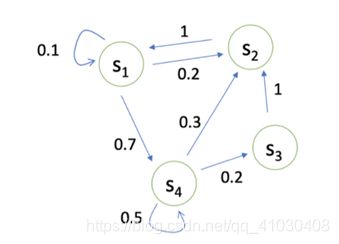
 图1.马尔科夫链示意图

如图1所示是一条马尔科夫链，比如s1状态之后的下一个状态，有0.1的概率留在s1,0.2的概率转移到s2，0.7的概率转移到s3。

我们可以用状态转移矩阵来描述状态转移p(st+1​=s′∣st​=s)：

  其实它每行描述的就是一个状态转移到其他所有状态的概率。

二、马尔可夫奖励过程(Markov Reward Process, MRP) 

MRP与MP相比，多了一个奖励函数。可以把MRP比作小船的随波逐流：小船放在水中，由于没有动力，所以会随波逐流。从当前状态开始，小船每到下一个状态，就可能产生一些奖励。

（1）相关术语

①Horizon：一个回合的长度（最大时间步数）；

②Return（回报）：区别于Reward，是每个状态的Reward折扣后的收益：

  那么，为什么要给奖励打个折扣之后才是最后的回报呢？

        1）首先，是有些马尔可夫过程是带环的，它并没有终结，然后我们想避免这个无穷的奖励；

        2）另外，后面的折扣表示了模型预测的不确定性；

        3）接上面一点，如果这个奖励是有实际价值的，我们可能是更希望立刻就得到奖励，而不是我们后面再得到奖励。

        4）还有在有些时候，这个系数也可以设为 0。当我们设为 0 过后，就只关注了它当前的奖励。我们也可以把它设为 1，设为 1 的话就是对未来并没有折扣，未来获得的奖励跟我们当前获得的奖励是一样的。

③当我们有了return，就可以定义状态的价值了。状态的价值函数定义为return的期望：

（2）Bellman Equation（贝尔曼等式）

贝尔曼等式描述了当前状态与未来状态的迭代关系，说明当前状态的价值函数可以由当前状态的奖励函数与下一个状态的价值函数求出，该式又叫做动态规划方程。此外，矩阵形式：

 具体推导过程不再赘述。由矩阵形式得到：

所以可以直接通过矩阵求逆的方法得到当前状态的价值，当然这样计算量很大，只适用于很小量的MRP。 

（3）Monte Carlo Algorithm（蒙特卡罗方法）

蒙特卡罗方法简单来说就是从当前状态让小船随波逐流，产生一条轨迹，从而得到对应的回报（产生的奖励乘于对应折扣），这样随机多次就可得到多条轨迹、多次回报，对多次回报求平均，即为当前状态的价值。这是从当前状态价值函数的定义角度去求解，当然随机次数要足够多。

（4）Iterative Algorithm（动态规划方法）

通过bootstrapping(自举)的方法进行迭代：利用贝尔曼方程，首先估计V’，然后用V’来估计V，从而不停迭代，直到当前状态与下一个状态的价值几乎相等，即收敛，停止迭代。

三、马尔可夫决策过程（MDP）

MDP可以比作一个小船在水中，但是此时不再是随波逐流，而是船上站了摆渡人，他会操纵小船的下一个动作。因此，相比于MP与MRP，MDP加入了agent，agent就是我们说的摆渡人，他会决定下一步的动作。

此时在价值函数的基础上，我们引入Q函数，定义为在某状态某动作条件下，对应return的期望。也就是在价值函数的条件之上，再加入动作action这一先决条件。

简单来说呢，马尔可夫决策过程可以解决两方面的问题：预测问题和控制问题。预测问题就是说，已知策略和MDP，求出每个状态的最佳价值函数。而控制问题则是未知策略，只有一个MDP，要求输出最佳价值函数以及最佳策略。事实上，要解决控制问题，也是在解决预测问题的基础上进行，无非是策略未知时要探索许多策略，然后对具体的一个策略求其最佳价值函数。

以上两个问题都可以通过动态规划的方法来解决。预测问题比较好解决，而对于控制问题，我们如何寻找最佳策略呢？

答：本质来说，当我们取得最佳的价值函数过后，我们可以通过对这个 Q 函数进行极大化，然后得到最佳的价值。然后，我们直接在这个Q函数上面取一个让这个action最大化的值，然后我们就可以直接提取出它的最佳的policy。

具体方法：

• 穷举法（一般不使用）：假设我们有有限多个状态、有限多个行为可能性，那么每个状态我们可以采取这个 A 种行为的策略，那么总共就是 |A|^{|S|}∣A∣∣S∣ 个可能的 policy。我们可以把这个穷举一遍，然后算出每种策略的 value function，然后对比一下可以得到最佳策略。但是效率极低。
• Policy iteration：一种迭代方法，有两部分组成，下面两个步骤一直在迭代进行，最终收敛：(有些类似于ML中EM算法（期望-最大化算法）)

第一个步骤是 policy evaluation ，即当前我们在优化这个 policy π ，所以在优化过程中得到一个最新的这个 policy 。

第二个步骤是 policy improvement ，即取得价值函数后，进一步推算出它的 Q 函数。得到 Q 函数过后，那我们就直接去取它的极大化。

• Value iteration: 我们一直去迭代 Bellman Optimality Equation，到了最后，它能逐渐趋向于最佳的策略，这是 value iteration 算法的精髓，就是我们去为了得到最佳的 v^*v∗ ，对于每个状态它的 v^*v∗ 这个值，我们直接把这个 Bellman Optimality Equation 进行迭代，迭代了很多次之后它就会收敛到最佳的policy以及其对应的状态，这里面是没有policy function的。

总结如上表所示，就对于 MDP 里面的 prediction 和 control 都是用动态规划来解，我们其实采取了不同的 Bellman Equation。

• 如果是一个 prediction 的问题，即 policy evaluation 的问题，直接就是不停地 run 这个 Bellman Expectation Equation，这样我们就可以去估计出给定的这个策略，然后得到价值函数。
• 对于 control，
  • 如果采取的算法是 policy iteration，那这里用的是 Bellman Expectation Equation 。把它分成两步，先上它的这个价值函数，再去优化它的策略，然后不停迭代。这里用到的只是 Bellman Expectation Equation。
  • 如果采取的算法是 value iteration，那这里用到的 Bellman Equation 就是 Bellman Optimality Equation，通过 arg max 这个过程，不停地去 arg max 它，最后它就会达到最优的状态。