BFS最小步数模型

---

最小步数模型

一、简介

最小步数模型和最短路模型的区别？

最短路模型：某一个点到另一个点的最短距离（坐标与坐标之间）

最小步数模型：不再是点（坐标），而是状态到另一个状态的转变

BFS难点所在（最短路问题）：

1. 存储的数据结构：队列

   状态如何存储到队列里边（以什么形式）?

2. 状态怎么表示，怎么转移?

3.dist

如何记录每一个状态的距离

**技巧：**在最小步数模型中状态和状态的距离通常用哈希表来进行存储（存在key-value的映射关系！），如map，unordered_map。

**思路：**将初始状态加入队列，然后去搜索扩展，直到搜索到目标状态为止。

注：

​ 在搜索过程中可能由状态的切换，如一维坐标切换到二维坐标，字符串切换到二标坐标形式的状态等等！

二、练习

1. 八数码

【题目链接】845. 八数码 - AcWing题库

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。

例如：

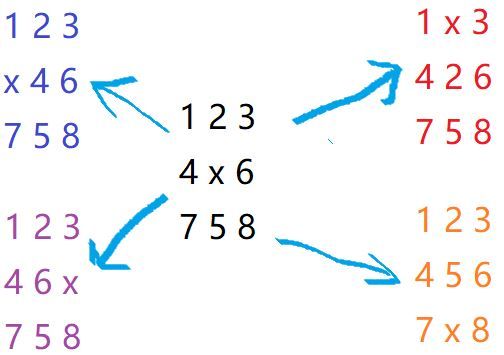
1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 3×33×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

1 2 3 
x 4 6 
7 5 8 

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 −1−1。

输入样例：

2  3  4  1  5  x  7  6  8

输出样例

19

1、题目的目标

求最小步数 -> 用BFS

2、移动情况

移动方式：

转以后：a = x + dx[i], b = y + dy[i].

思想：把每一个状态看作图论的一个节点（节点a到节点b的距离为1——状态能转移）——> 起点到终点最少需要多少步

从初始状况移动到目标情况 —> 求最短路

3、问题

第一点：状态如何存储到队列里？

第二点：如何记录每一个状态的“距离”（即需要移动的次数）？

第三点：队列怎么定义（队列存储的是状态，状态可以用字符串表示），dist数组怎么定义（每一个状态到起始状态的距离——两个关键字：状态(字符串)、距离(int)）——key-value？——哈希表

4、解决方案

将 “3*3矩阵” 转化为 “字符串”

如：

所以：

队列可以用 queue
//直接存转化后的字符串
dist数组用 unordered_map
//将字符串和数字联系在一起，字符串表示状态，数字表示距离

5、矩阵与字符串的转换方式

【参考代码】

#include 
#include 
#include 
#include 
#include

using namespace std;

//状态转移
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int bfs(string strat)
{
    //定义目标状态、
    string end = "12345678x";
    //定义队列和dist数组
    queue q;
    unordered_map d;
    
    //初始化队列和dist数组
    q.push(strat);
    d[strat] = 0;
    
    while(q.size())
    {
        // 获取队头元素，弹出队列
        auto t = q.front();
        q.pop();
        //记录当前状态的距离，如果为最终状态则返回距离结果
        int distance = d[t];
        if(t == end) return d[t];
        
        //查询x在一位数组中的下标，进行状态转换
        int k = t.find('x');
        int x = k / 3, y = k % 3;
        
        //扩展队头元素（邻接节点入队）
        for(int i = 0; i < 4; i ++)
        {
            //转移后的x的坐标（邻接节点）
            int a = x + dx[i], b = y + dy[i];
            //没有越界
            if(a >= 0 && b >= 0 && a < 3 && b < 3)
            {
                //转移x
                swap(t[k], t[a * 3 + b]);
                //如果当前状态是第一次遍历，记录距离，入队
                if(!d.count(t))
                {
                    d[t] = distance + 1;
                    q.push(t);
                }
                //还原状态，为下一种转换情况做准备！
                swap(t[k], t[a * 3 + b]);
            }
        }
    }
    
    //无法转换到目标状态，返回-1
    return -1;
    
}

int main()
{
    
    string strat;
    // 输入起始状态
    for (int i = 0; i < 9; i ++ )
    {
        char c;
        cin >> c;
        strat += c;
    }
    
    cout << bfs(strat);
    
}

2.魔板

【题目链接】1107. 魔板 - AcWing题库

Rubik 先生在发明了风靡全球的魔方之后，又发明了它的二维版本——魔板。

这是一张有 8 个大小相同的格子的魔板：

1 2 3 4
8 7 6 5

我们知道魔板的每一个方格都有一种颜色。

这 8 种颜色用前 8 个正整数来表示。

可以用颜色的序列来表示一种魔板状态，规定从魔板的左上角开始，沿顺时针方向依次取出整数，构成一个颜色序列。

对于上图的魔板状态，我们用序列 (1,2,3,4,5,6,7,8) 来表示，这是基本状态。

这里提供三种基本操作，分别用大写字母 A，B，C 来表示（可以通过这些操作改变魔板的状态）：

A：交换上下两行；
B：将最右边的一列插入到最左边；
C：魔板中央对的4个数作顺时针旋转。

下面是对基本状态进行操作的示范：

A：

8 7 6 5
1 2 3 4

B：

4 1 2 3
5 8 7 6

C：

1 7 2 4
8 6 3 5

对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到特殊状态的转换，输出基本操作序列。

注意：数据保证一定有解。

输入格式

输入仅一行，包括 8 个整数，用空格分开，表示目标状态。

输出格式

输出文件的第一行包括一个整数，表示最短操作序列的长度。

如果操作序列的长度大于0，则在第二行输出字典序最小的操作序列。

数据范围

输入数据中的所有数字均为 1 到 88 之间的整数。

输入样例：

2 6 8 4 5 7 3 1

输出样例：

7
BCABCCB

思路：

• 将初始状态加入队列，然后去搜索扩展，直到搜索到目标状态为止。每一次扩展ABC三种操作后，如果该状态没被遍历过，更新最短距离并加入队列。

• 由于要存储路径，因此我们开一个pre数组，记录当前状态的前驱状态，最终由终点逆推回去即可获得整个路径（上一篇博客的迷宫问题也是存储路径），在记录前驱状态的同时也把操作方式记录下来

• 状态的存储：看代码解释

• 状态的切换：字符串与一个2行4列的一个二维表的相互切换，以这个二维表为桥梁具体实现A、B、C三种操作

我们只需要按照先进行操作A，再B后C的操作顺序，最终得到的结果就会满足字典序最小。

【代码实现】

#include 
#include 
#include 
#include 
#include 

using namespace std;

char g[2][4];//状态图(状态图作为操作状态转换的一个桥梁)
// key-value
unordered_map<string, int> dist;// 记录到当前状态的最小步数
unordered_map<string, pair<char, string>> pre;// 存储当前状态的前驱，和操作方式
queue<string>q;

//在操作前 先把字符串变化到 2行4列的图表状态，方便我们操作的实现
void set(string state)
{
    for(int i = 0; i < 4; i ++) g[0][i] = state[i];
    for(int i = 7, j = 0; j < 4; i --, j ++) g[1][j] = state[i];
}
//在set得到的图基础上 在进行了ABC操作后得到新的状态图 将改图转换为状态字符串,最为操作后得到的字符串结果返回
string get()
{
    string res;
    for(int i = 0; i < 4; i ++) res += g[0][i];
    for(int j = 3; j >= 0; j --) res += g[1][j];  
    return res;
}


string move0(string state)//操作A：交换上下两行
{
    set(state);
    for(int i = 0; i < 4; i ++) swap(g[0][i], g[1][i]);
    return get();
}

string move1(string state)//操作B:将最右边的一列插入到最左边
{
    set(state);
    //(先将最后一列存下来，将前3列后移一列，最后一列移到最左边)
    char v0 = g[0][3], v1 = g[1][3];
    for(int i = 3; i >= 0; i --)
    {
        g[0][i] = g[0][i - 1];
        g[1][i] = g[1][i - 1];
    }
    g[0][0] = v0, g[1][0] = v1;
    return get();
}

string move2(string state)//操作C：魔板中央对的4个数作顺时针旋转
{
    set(state);
    char v = g[0][1];
    g[0][1] = g[1][1];
    g[1][1] = g[1][2];
    g[1][2] = g[0][2];
    g[0][2] = v;
    return get();
    
}

int bfs(string start, string end)
{
    if(start == end) return 0;//如果一开始的状态即为目标状态

    q.push(start);
    dist[start] = 0;
    
    //扩展队头元素
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        
        //每种状态有三种操作方式，每次操作后得到对应的字符串结果
        string m[3];
        m[0] = move0(t);
        m[1] = move1(t);
        m[2] = move2(t);
        
        //遍历三种状态方式，看看选哪个（按照先A后B再C操作得到的结果满足字典序从小到大）
        for(int i = 0; i < 3; i ++)
        {
            if(!dist.count(m[i]))//如果这个状态没有被遍历过
            {
                q.push(m[i]);
                dist[m[i]] = dist[t] + 1;//更新步数
                pre[m[i]] = {'A' + i ,t};//将操作方式，是该邻接点的前驱记录下来
                if(m[i] == end) return dist[end];// 如果在遍历中发现已经到达目标状态直接返回结果
            }
        }
        
    }
    
    return -1;
}

int main()
{
    string start, end;
    start = "12345678";
    for(int i = 0; i < 8; i ++)
    {
        int x;
        cin >> x;
        end += (x + '0');
    }
    // cout << end << endl;
    
    int step = bfs(start, end);
    cout << step << endl;
    
    //通过终点的前驱逐一反推获取操作的方式
    string res;
    while (end != start)
    {
        res += pre[end].first;//操作
        end = pre[end].second;//状态字符串
    }

    reverse(res.begin(), res.end());//由于是逆推求前驱，因此结果要翻转

    if (step > 0) cout << res << endl;
    
    return 0;
}

3. 两种操作

【题目链接】acwing4300
思路：最短路模型

• n = m 0
• 当n > m时，只能减一操作，答案即为n-m
• 当n < m时：先让n变大，但不能一直乘2
  -----当2*n < m时优先乘2操作
  -----当2*n > m时优先减一操作

我们宽搜的范围是两万！

【代码实现】

#include 
#include 
#include 
#include 

using namespace std;

int n, m;
const int N = 20010;
int dist[N];

int bfs()
{
    memset(dist, 0x3f, sizeof dist);
    dist[n] = 0;
    
    queue<int>q;
    q.push(n);
    
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        
    
        if(t == m) return dist[m];
        
        if(2 * t < N && dist[2 * t] > dist[t] + 1)
        {
            q.push(2 * t);
            dist[2 * t] = dist[t] + 1;
        }
        
        if(t > 1 && dist[t - 1] > dist[t] + 1)
        {
            q.push(t - 1);
            dist[t - 1] = dist[t] + 1;
        }
        
    }
    
}

int main()
{
    
    cin >> n >> m;
    if(n > m) cout << n - m;
    else cout << bfs();
    return 0;
}

4.D - Multiply and Rotate

【题目链接】D - 乘法和旋转 (atcoder.jp)

题目意思：

给定初始值为 x = 1， 两种操作方式

• 第一种是将 x 替换为 a * x,
• 第二种是将 x 视为字符串，当前仅当满足 x 大于等于 10且x 不能被 10 整除， 将 x 的最右端字符放到最左端。

求解 由x = 1变到N 时的最小操作次数。

思路：

初始状态1，目标状态N

BFS最小步数模型，状态为操作1的相乘和操作2的换位（根据题意转为字符串后将换位拼接即可）

注：

a与N的范围都在2~10^6之间，对于操作1，当 当前状态 * a（相乘）可能会导致结果溢出，为此要直接开long long

【代码实现】

#include
#include
#include
#include
#include

using namespace std;

queue<int> q;
const int N = 1e6 + 10;

typedef long long LL;

int d[N];
bool st[N];

LL a, n; // 为了防止 a 与 N 相乘结果溢出 直接开long long！  坑啊！  

int bfs()
{
	q.push(1);
	d[1] = 0;
	
	while(q.size())
	{
		auto t = q.front();
		q.pop();
		
		if(t == n) return d[n];
		
		if(st[t]) continue;
		st[t] = true;
		// 宽搜的范围
		//扩展队头元素
		if( t * a <= N)
		{
			q.push(t * a);
			d[t * a] = d[t] + 1;	
		}
		if(t > 10 && t % 10 != 0)
		{
			string str = to_string(t);
			int len = str.size();
			char a = str[len - 1];
			string newStr = a + str.substr(0, len - 1);	
			int nums = stoi(newStr);
			q.push(nums);
			d[nums] = d[t] + 1;
		} 
	}
	
	return -1;
	
}

int main()
{
	cin >> a >> n;
	
	cout << bfs();
	
	return 0;
}

三、总结

最小步数模型的难点在于状态的表示、切换还有存储，理清它们之间的逻辑关系代码就好实现了！

技巧：一维数组与二维数组坐标的转换

设[一维数组]下标为index（从0开始），二维数组长度为m * n，则：

一维数组转换为二维数组

x = index / n 
y = index % n

二维数组转换为一维数组

index = x + y * n

**技巧：**在最小步数模型中状态和状态的距离通常用哈希表来进行存储（存在key-value的映射关系！），如map，unordered_map。

**技巧：**BFS存储路径问题，通常通过设置一个前驱pre数组来记录当前节点或者状态的前驱，最后再逆推找出路径

学习内容参考：
acwing算法基础课、提高课
acwing周赛
atcoder比赛

注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦

欢迎访问：本人博客园地址