字节跳动 | 游戏研发岗第一批笔试(题解)
字节游戏研发岗笔试第一批:2小时4题,满分一百,不能使用本地ide,代码为acm模式
第一题_走迷宫(20分)
题面
给出长n宽m的迷宫(n和m都在1~500之间),迷宫由0和1组成,1表示有墙不能走,0表示能走。WASD分别表示向上下左右移动,给出由WASD组成的长度为q的字符串,表示走的方向。小红初始位置在迷宫的左上角(1,1),求按照字符串表示的方向走完之后,小红在迷宫的最终位置;
样例
样例输入
3 3 4
000
100
001
WDDS
正确输出
2 3
思路
模拟,值得注意的有3点:
- 地图的范围是(1~n)(1~m),要把周围 0行 0列 n+1行 m+1列 那几部分设成1,表示边界,防止走出边界
- 在读入二维矩阵的时候,
- 模拟小红走迷宫的时候要预判能否走动,能走动的话改变坐标
代码
#include
using namespace std;
int n,m,q,a[510][510];
string s;
int main() {
cin >> n >> m >> q;
int x=1, y=1; //小红的起始位置
//预处理边界和迷宫
for(int i=0; i<=501; i++)
for(int j=0; j<=501; j++)
a[i][j]=1; //0~501是为了把周围部分设成1表示边界(想象有个围墙把迷宫围了起来)
/*由于之前把表示迷宫的数组预处理了,现在想把需要读入的0/1排列
赋值给a[][]以表示迷宫。这里我们借用一个0/1字符串对a[][]按位赋值*/
for(int i=1; i<=n; i++) {
string t;
//每行读入一个0/1字符串,再按位赋值给a[][]
cin >> t;
for(int j=1; j<=m; j++)
a[i][j] = t[j-1] == '0' ? 0 : 1;
}
cin >> s; //读入表示行走方向的字符串
for(auto it : s) {
if(it=='W' && !a[x-1][y]) x--; //预判能否向上走,若能,向上移动
if(it=='S' && !a[x+1][y]) x++; //预判能否向下走,若能,向下移动
if(it=='A' && !a[x][y-1]) y--; //预判能否向左走,若能,向左移动
if(it=='D' && !a[x][y+1]) y++; //预判能否向右走,若能,向右移动
}
cout << x << " " << y << "\n"; //输出小红最后所在的位置
return 0;
} 第二题_输出序列(20分)
题面
给出n个数,每个数为1~n中某一个且这些数各不相同,要求构造一条k对相邻和为奇数的序列,输出一种合法的即可
样例
样例输入
8 4
正确输出
1 2 3 4 6 8 5 7
思路
- 我们首先要知道,奇偶交错排列才能保证相邻和为奇数,奇奇或偶偶的和只能为偶数;
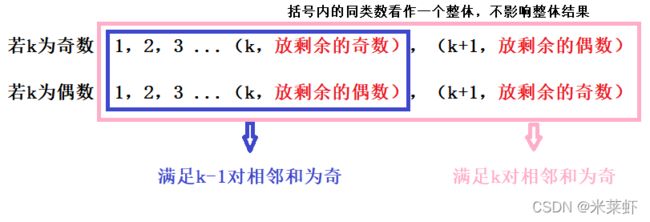
- 其次,要满足k对相邻和为奇数的序列,考虑输出1~k+1;
- 再保证剩下的数不增加相邻和为偶数对就可以了。
- 下面用一幅图表示一下具体的做法:
代码
#include
using namespace std;
int main()
{
int n,k;
cin>>n>>k;
if(k%2!=0) { //若k为奇数,k+1为偶数
for(int i=1; i<=k; i++) cout< 第三题_字符串染色(30分)
题面
给出一个字符串S,由R和B组成,不同下标对应不同权值,求通过改变B为R,使得连续R的区间长度至少为K的权值花费的最小值
样例输入
B B R R B R B R
1 3 5 6 7 4 2 9
4
输出
7
思路
固定长度K,然后扫一遍,用双指针操作
两大类 “双指针” 算法剖析【附例题详解+AC代码】_夏旭的博客-CSDN博客首先,介绍一下双指针算法。我们在用朴素算法暴力解决问题时,通过挖掘某些性质,使得算法复杂度由 O(n^2)->O(n) ,我们把具有这样性质的算法称为双指针算法【其实双指针算法非常广泛,不只是被用在维护两个窗口上,但在这里,我们缩小了它的范围】。常用的两种双指针算法的类型:一种是: 两个指针分别指向两个序列 ( “归并排序” 就用到了这一种指针,具体操作:每一次分别移动两个指针,两个指针移动完的时候,排序过程即结束);另一种是: 两个指针指向同一个序列,一个指向开头,一个指向结尾 (如快排)。https://blog.csdn.net/Luoxiaobaia/article/details/106182893
第四题_走象棋(30分)
题面
大概是给出象棋中的象的始末位置,判断路径是否合法,合法则求最短距离,写了但没有分。不太回忆得起来了...大概就是一个最短路径的搜索算法
下面给出常见搜索算法的几种类型(日后补充对应题型):
BFS与DFS
- BFS:这是一种基于队列这种数据结构的搜索方式,它的特点是由每一个状态可以扩展出许多状态,然后再以此扩展,直到找到目标状态或者队列中头尾指针相遇,即队列中所有状态都已处理完毕。
- DFS:基于递归的搜索方式,它的特点是由一个状态拓展一个状态,然后不停拓展,直到找到目标或者无法继续拓展结束一个状态的递归。
广度优先搜索-BFS
它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域。
适用于迷宫类问题。
链接:http://blog.csdn.net/raphealguo/article/details/7523411
深度优先搜索-DFS
http://blog.csdn.net/ns_code/article/details/19617187
Floyd-Warshall算法
任意两个点之间最短路径。它的时间复杂度是O(N3)。求指定两点之间的最短路或者指定一个点到其余各个顶点的最短路径也是可行的。
对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立。
链接:http://developer.51cto.com/art/201403/433874.htm
Dijkstra(迪杰斯特拉)算法
是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
Dijksra的算法是一个贪婪算法,时间复杂度是O(VLogV)(使用最小堆)。
链接:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
Bellman-Ford
在网络路由中,该算法会被用作距离向量路由算法。
Bellman-Ford也比迪杰斯特拉算法更简单和同时也适用于分布式系统。但Bellman-Ford的时间复杂度是O(VE),E为边的个数,这要比迪杰斯特拉算法慢。
spfa算法
时间复杂度为O(ke),k为所以顶点进队的平均次数,k一般小于等于2
链接:http://www.360doc.com/content/13/1208/22/14357424_335569176.shtml
最小生成树问题
Kruskal算法,贪心算法;
Prim算法,其从某一源点出发,维持一个集合A(A内结点构成一棵树),算法每次选择从A出发到A外的结点中的一条权重最小的边,然后将这条边加入集合A中。
http://blog.csdn.net/tostq/article/details/52733071
A*算法
A*算法与BFS:可以这样说,BFS是A*算法的一个特例。对于一个BFS算法,从当前节点扩展出来的每一个节点(如果没有被访问过的话)都要放进队列进行进一步扩展。也就是说BFS的估计函数h永远等于0,没有一点启发式的信息,可以认为BFS是“最烂的”A*算法。
链接:http://www.cppblog.com/mythit/archive/2009/04/19/80492.aspx