OpenCV学习笔记(十五)——k近邻算法

K 近邻算法是最简单的机器学习算法之一，主要用于将对象划分到已知类中，在生活中被广泛使用。例如，教练要选拔一批长跑运动员，如何选拔呢？他使用的可能就是K 近邻算法，会选择个子高、腿长、体重轻，膝、踝关节围度小，跟腱明显，足弓较大者作为候选人。他会觉得这样的孩子有运动员的潜质，或者说这些孩子的特征和运动员的特征很接近。

1. 理论基础

例如，已知某知名双胞胎艺人A 和B 长得很像，如果要判断一张图像T 上的人物到底是艺人A 还是艺人B，则采用K 近邻算法实现的具体步骤如下：

1. 收集艺人A 和艺人B 的照片各100 张。
2. 确定几个用来识别人物的重要特征，并使用这些特征来标注艺人A 和B 的照片。例如，根据某4 个特征，每张照片可以表示为[156, 34, 890, 457]这样的形式（即一个样本点）。按照上述方式，获得艺人A 的100 张照片的数据集FA，艺人B 的100 张照片的数据集FB。此时数据集FA、FB 中的元素都是上述特征值的形式，每个集合中各有100 个这样的特征值。简而言之，就是使用数值来表示照片，得到艺人A 的数值特征集（数据集）FA、艺人B 的数值特征集FB。
3. 计算待识别图像T 的特征，并使用特征值表示图像T。例如，图像T 的特征值TF 可能为[257, 896, 236, 639]。
4. 计算图像T 的特征值TF 与FA、FB 中各特征值之间的距离。
5. 找出产生其中k 个最短距离的样本点（找出离T 最近的k 个邻居），统计k 个样本点中属于FA 和FB 的样本点个数，属于哪个数据集的样本点多，就将T 确定为哪个艺人的图像。例如，找到11 个最近的点，在这11 个点中，属于FA 的样本点有7 个，属于FB 的样本点有4个，那么就确定这张图像T 上的艺人为A；反之，如果这11 个点中，有6 个样本点属于FB，有5 个样本点属于FA，那么就确定这张图像T 上的艺人为B。

以上所述就是K 近邻算法的基本思想。

2. 计算

计算机的“感觉”是通过逻辑计算和数值计算来实现的。所以，在大多数的情况下，我们要对计算机要处理的对象进行数值化处理，将其量化为具体的值，以便后续处理。比较典型的方法是取某几个固定的特征，然后将这些特征量化。

K 近邻算法在获取各个样本的特征值之后，计算待识别样本的特征值与各个已知分类的样本特征值之间的距离，然后找出k 个最邻近的样本，根据k 个最邻近样本中占比最高的样本所属的分类，来确定待识别样本的分类。

2.1 归一化

通常情况下，由于各个参数的量纲不一致等原因，需要对参数进行处理，让所有参数具有相等的权值。

一般情况下，对参数进行归一化处理即可。做归一化时，通常使用特征值除以所有特征值中的最大值（或者最大值与最小值的差）。

2.2 距离计算

这里计算距离采用欧氏距离即可，即计算平方和的平方根。

例如，有(身高,体重)形式的特征值A(185, 75)和B(175, 86)，下面判断C(170, 80)与特征值A 和特征值B 的距离：

• C与A 的距离：
  $$\sqrt{\left(185-170\right){}^2+\left(75-80\right){}^2}$$
• C与B 的距离：
  $$\sqrt{\left(175-170\right){}^2+\left(86-80\right){}^2}$$

3. 手写数字识别原理

假设我们要让程序识别下图中上方的数字（当然，你一眼就知道是“8”，但是现在要让计算机识别出来）。识别的方式是，依次计算该数字图像（即写有数字的图像）与下方数字图像的距离，与哪个数字图像的距离最近（此时k =1），就认为它与哪幅图像最像，从而确定这幅图像中的数字是多少。

下面分别从特征值提取和数字识别两方面展开介绍。

3.1 特征值提取

步骤 1：我们把数字图像划分成很多小块，如下图所示。该图中每个数字被分成5 行4列，共计5×4 = 20 个小块。此时，每个小块是由很多个像素点构成的。当然，也可以将每一个像素点理解为一个更小的子块。

为了叙述上的方便，将这些小块表示为B（Bigger），将B 内的像素点，记为S（Smaller）。因此，待识别的数字“8”的图像可以理解为：

• 由 5 行4 列，共计5×4=20 个小块B 构成。
• 每个小块 B 内其实是由M×N 个像素（更小块S）构成的。为了描述上的方便，假设每个小块大小为10×10 =100 个像素。

步骤 2：计算每个小块B 内，有多少个黑色的像素点。或者这样说，计算每个小块B 内有多少个更小块S 是黑色的。

• 第 1 个小块B 共有0 个像素点（更小块S）是黑色的，记为0。
• 第 2 个小块B 共有28 个像素点（更小块S）是黑色的，记为28。
• 第 3 个小块B 共有10 个像素点（更小块S）是黑色的，记为10。
• 第 4 个小块B 共有0 个像素点（更小块S）是黑色的，记为0。

以此类推，计算出数字“8”的图像中每一个小块B 中有多少个像素点是黑色的。

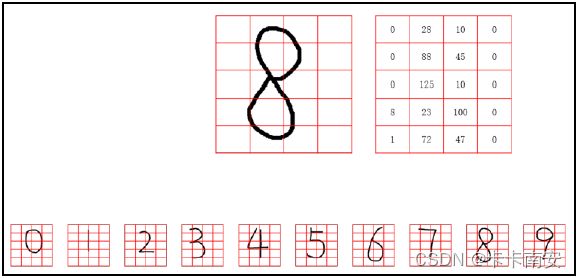
不同的数字图像中每个小块B 内黑色像素点的数量是不一样的。正是这种不同，使我们能用该数量（每个小块B 内黑色像素点的个数）作为特征来表示每一个数字。

步骤 3：有时，为了处理上的方便，我们会把得到的特征值排成一行（写为数组形式）。

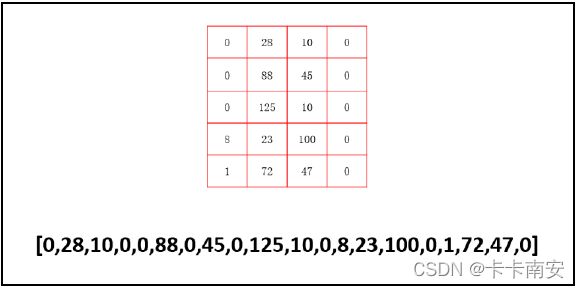
当然，在Python 里完全没有必要这样做，因为Python 可以非常方便地直接处理图中上方数组（array）形式的数据。这里为了说明上的方便，仍将其特征值处理为一行数字的形式。

经过上述处理，数字“8”图像的特征值变为一行数字，如图所示。

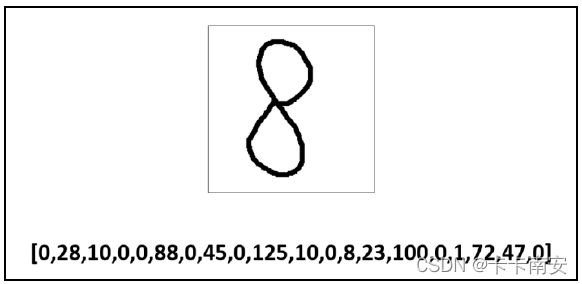
步骤 4：与数字“8”的图像类似，每个数字图像的特征值都可以用一行数字来表示。从某种意义上来说，这一行数字类似于我们的身份证号码，一般来说，具有唯一性。

3.2 数字识别

数字识别要做的就是比较待识别图像与图像集中的哪个图像最近。这里，最近指的是二者之间的欧氏距离最短。

本例中为了便于说明和理解进行了简化，将原来下方的10 个数字减少为2 个（也即将分类从10 个减少为2 个）。假设要识别的图像为图中上方的数字“8”图像，需要判断该图像到底属于图中下方的数字“8” 图像的分类还是数字“7”图像的分类。

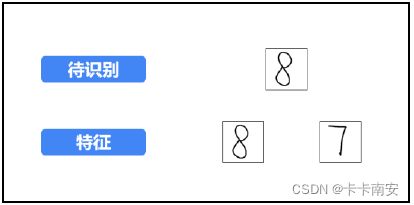
步骤 1：提取特征值，分别提取待识别图像的特征值和特征图像的特征值。

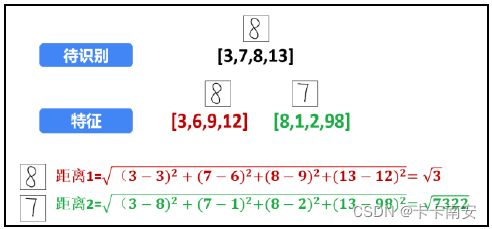
为了说明和理解上的方便，将特征进行简化，每个数字图像只提取4 个特征值（划分为2×2 = 4 个子块B），如图所示。此时，提取到的特征值分别为：

步骤 2：计算待识别图像与特征图像之间的距离。

首先，计算待识别的数字“8”图像与下方的数字“8”特征图像之间的距离，如图所示。计算二者之间的距离：

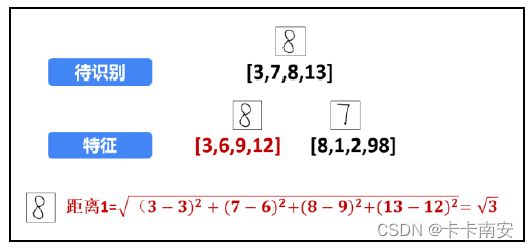
接下来，计算待识别的数字“8”图像与数字“7”特征图像之间的距离，如图所示。二者之间的距离为：

步骤 3：识别。

根据计算的距离，待识别的数字“8”图像与数字“8”特征图像的距离更近。所以，将待识别的数字“8”图像识别为数字“8”特征图像所代表的数字“8”。

上面介绍的是K 近邻算法只考虑最近的一个邻居的情况，相当于K 近邻中k =1 的情况。在实际操作中，为了提高可靠性，需要选用大量的特征值。例如，每个数字都选用不同的形态的手写体100 个，对于0 ~ 9 这10 个数字，共需要100×10 =1000幅特征图像。在识别数字时，分别计算待识别的数字图像与这些特征图像之间的距离。这时，可以将k 调整为稍大的值，例如k =11，然后看看其最近的11 个邻居分属于哪些特征图像。例如，其中：

• 有 8 个属于数字“6”特征图像。
• 有 2 个属于数字“8”特征图像。
• 有 1 个属于数字“9”特征图像。

通过判断，当前待识别的数字为数字“6”特征图像所代表的数字“6”。

3. 自定义函数手写数字识别

OpenCV 提供了函数cv2.KNearest()用来实现K 近邻算法，在OpenCV 中可以直接调用该函数。为了进一步了解K 近邻算法及其实现方式，本节首先使用Python 和OpenCV 实现一个识别手写数字的实例。

在本例中，0~9 的每个数字都有10 个特征值。例如，数字“0”的特征值如图所示。为了便于描述，将所有这些用于判断分类的图像称为特征图像。

下面分步骤实现手写数字的识别。

3.1 数据初始化

对程序中要用到的数据进行初始化。涉及的数据主要有路径信息、图像大小、特征值数量、用来存储所有特征值的数据等。

本例中：

• 特征图像存储在当前路径的“image”文件夹下。
• 用于判断分类的特征值有100 个（对应100 幅特征图像）。
• 特征图像的行数（高度）、列数（宽度）可以通过程序读取。也可以在图像上单击鼠标右键后通过查找属性值来获取。这里采用设置好的特征图像集，每个特征图像都是高240 行、宽240 列。

根据上述已知条件，对要用到的数据初始化：

s='image\\' # 图像所在的路径
num=100 # 共有特征值的数量
row=240 # 特征图像的行数
col=240 # 特征图像的列数
a=np.zeros((num,row,col)) # a 用来存储所有特征的值

3.2 读取特征图像

本步骤将所有的特征图像读入到a 中。共有10 个数字，每个数字有10 个特征图像，采用嵌套循环语句完成读取。具体代码如下：

n=0 # n 用来存储当前图像的编号。
for i in range(0,10):
	for j in range(1,11):
		a[n,:,:]=cv2.imread(s+str(i)+'\\'+str(i)+'-'+str(j)+'.bmp',0)
		n=n+1

3.3 提取特征图像的特征值

在提取特征值时，可以计算每个子块内黑色像素点的个数，也可以计算每个子块内白色像素点的个数。这里我们选择计算白色像素点（像素值为255）的个数。按照上述思路，图像映射到特征值的关系如图所示。

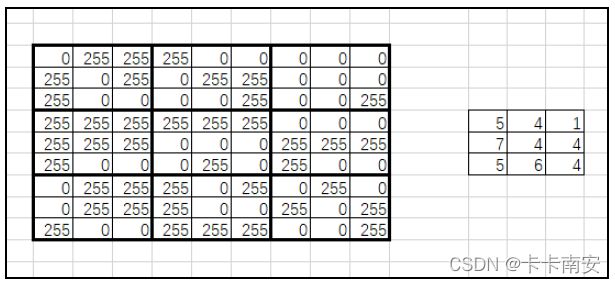
这里需要注意，特征值的行和列的大小都是原图像的1/5。所以，在设计程序时，如果原始图像内位于(row, col)位置的像素点是白色，则要把对应特征值内位于(row/5, col/5)处的值加1。

根据上述分析，编写代码如下：

feature=np.zeros((num,round(row/5),round(col/5))) # feature 存储所有样本的特征值
#print(feature.shape) # 在必要时查看feature 的形状是什么样子
#print(row) # 在必要时查看row 的值，有多少个特征值（100 个）
for ni in range(0,num):
	for nr in range(0,row):
		for nc in range(0,col):
			if a[ni,nr,nc]==255:
				feature[ni,int(nr/5),int(nc/5)]+=1
f=feature #简化变量名称

3.4 计算待识别图像的特征值

读取待识别图像，然后计算该图像的特征值。编写代码如下：

o=cv2.imread('image\\test\\9.bmp',0) # 读取待识别图像
# 读取图像的值
of=np.zeros((round(row/5),round(col/5))) # 用来存储待识别图像的特征值
for nr in range(0,row):
	for nc in range(0,col):
		if o[nr,nc]==255:
			of[int(nr/5),int(nc/5)]+=1

3.5 计算待识别图像与特征图像之间的距离

依次计算待识别图像与特征图像之间的距离。编写代码如下：

d=np.zeros(100)
for i in range(0,100):
	d[i]=np.sum((of-f[i,:,:])*(of-f[i,:,:]))

数组 d 通过依次计算待识别图像特征值of 与数据集f 中各个特征值的欧氏距离得到。数据集f 中依次存储的是数字0~9 的共计100 个特征图像的特征值。所以，数组d 中的索引号对应着各特征图像的编号。例如，d[mn]表示待识别图像与数字“m”的第n 个特征图像的距离。数组d 的索引与特征图像之间的对应关系如表所示。

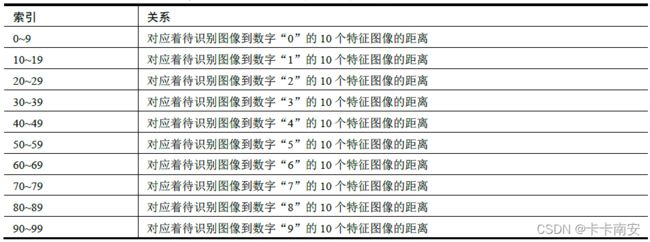
如果将索引号整除10，得到的值正好是其对应的特征图像上的数字。例如d[34]对应着待识别图像到数字“3”的第4 个特征图像的欧式距离。而将34 整除10，得到int(34/10) = 3，正好是其对应的特征图像上的数字。

确定了索引与特征图像的关系，下一步可以通过计算索引达到数字识别的目的。

3.6 获取k个最短距离及其索引

从计算得到的所有距离中，选取k 个最短距离，并计算出这k 个最短距离对应的索引。具体实现方式是：

• 每次找出最短的距离（最小值）及其索引（下标），然后将该最小值替换为最大值。
• 重复上述过程k 次，得到k 个最短距离对应的索引。

每次将最小值替换为最大值，是为了确保该最小值在下一次查找最小值的过程中不会再次被找到。例如，要在数字序列“11, 6, 3, 9”内依次找到从小到大的值。

• 第 1 次找到了最小值“3”，同时将“3”替换为“11”。此时，要查找的序列变为“11, 6, 11, 9”。
• 第 2 次查找最小值时，在序列“11, 6, 11, 9”内找到的最小值是数字“6”，同时将“6”替换为最大值“11”，得到序列“11,11,11,9”

不断地重复上述过程，依次在第3 次找到最小值“9”，在第4 次找到最小值“11”。当然，在本例中查找的是数值，具体实现时查找的是索引值。

d=d.tolist()
temp=[]
Inf = max(d)
#print(Inf)
k=7
for i in range(k):
	temp.append(d.index(min(d)))
	d[d.index(min(d))]=Inf

3.7 识别

根据计算出来的k 个最小值的索引，结合上面的表格就可以确定索引所对应的数字。具体实现方法是将索引值整除10，得到对应的数字。

例如，在k =11 时，得到最小的11 个值所对应的索引依次为：66、60、65、63、68、69、67、78、89、96、32。它们所对应的特征图像如表所示。

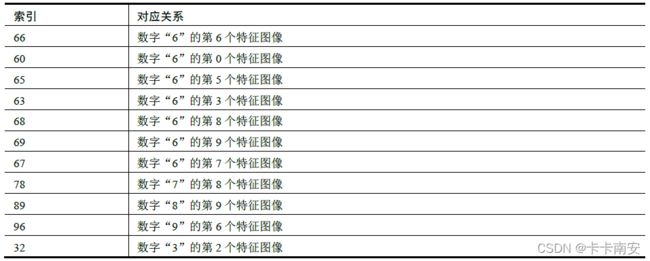
上述结果说明，与待识别图像距离最近的特征图像中，有7 个是数字“6”的特征图像。所以，待识别图像是数字“6”。

下面讨论如何通过程序识别数字。已知将索引整除10，就能得到对应特征图像上的数字，因此对于上述索引整除10：
(66, 60, 65, 63, 68, 69, 67, 78, 89, 96, 32)整除10 = (6, 6, 6, 6, 6, 6, 6, 7, 8, 9, 3)

为了叙述上的方便，将上述整除结果标记为dr，在dr 中出现次数最多的数字，就是识别结果。对于上例，dr 中“6”的个数最多，所以识别结果就是数字“6”。

这里我们借助索引判断一组数字中哪个数字出现的次数最多：

• 建立一个数组r，让其元素的初始值都是0。
• 依次从 dr 中取数字n，将数组r 索引位置为n 的值加1。例如，从dr 中取到的第1 个数字为“6”，将r[6]加上1；从dr 中取到第2 个数字也为“6”，将r[6]加上1；以此类推，对于dr=[6, 6, 6, 6, 6, 6, 6, 7, 8, 9, 3]，得到数组r 的值为[0, 0, 0, 1, 0, 0, 7, 1, 1, 1]。

在数组 r 中：

• r[0]=0，表示在dr 中不存在值为0 的元素。
• r[3]=1，表示在dr 中有1 个“3”。
• r[6]=7，表示在dr 中有7 个“6”。
• r[7]=1，表示在dr 中有1 个“7”。
• r[8]=1，表示在dr 中有1 个“8”。
• r[9]=1，表示在dr 中有1 个“9”。
• r 中其余为0 的值，表示其对应的索引在dr 中不存在。

temp=[i/10 for i in temp]
# 数组r 用来存储结果，r[0]表示K 近邻中“0”的个数，r[n]表示K 近邻中“n”的个数
r=np.zeros(10)
for i in temp:
	r[int(i)]+=1
print('当前的数字可能为:'+str(np.argmax(r)))

3.8 完整代码

import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取样本（特征）图像的值
s='image\\' # 图像所在路径
num=100 # 样本总数
row=240 # 特征图像的行数
col=240 # 特征图像的列数
a=np.zeros((num,row,col)) # 存储所有样本的数值
#print(a.shape)
n=0 # 存储当前图像的编号
for i in range(0,10):
	for j in range(1,11):
		a[n,:,:]=cv2.imread(s+str(i)+'\\'+str(i)+'-'+str(j)+'.bmp',0)
		n=n+1
#提采样本图像的特征
feature=np.zeros((num,round(row/5),round(col/5))) # 用来存储所有样本的特征值
#print(feature.shape) # 看看特征值的形状是什么样子
#print(row) # 看看row 的值，有多少个特征值（100）

for ni in range(0,num):
	for nr in range(0,row):
		for nc in range(0,col):
			if a[ni,nr,nc]==255:
				feature[ni,int(nr/5),int(nc/5)]+=1
f=feature # 简化变量名称
#####计算当前待识别图像的特征值
o=cv2.imread('image\\test\\5.bmp',0) # 读取待识别图像
##读取图像值
of=np.zeros((round(row/5),round(col/5))) # 存储待识别图像的特征值
for nr in range(0,row):
	for nc in range(0,col):
		if o[nr,nc]==255:
			of[int(nr/5),int(nc/5)]+=1
###开始计算，识别数字，计算最邻近的若干个数字是多少，判断结果
d=np.zeros(100)
for i in range(0,100):
	d[i]=np.sum((of-f[i,:,:])*(of-f[i,:,:]))
#print(d)
d=d.tolist()
temp=[]
Inf = max(d)
#print(Inf)
k=7
for i in range(k):
	temp.append(d.index(min(d)))
	d[d.index(min(d))]=Inf
#print(temp) #看看都被识别为哪些特征值
temp=[i/10 for i in temp]
# 也可以返回去处理为array，使用函数处理
#temp=np.array(temp)
#temp=np.trunc(temp/10)
#print(temp)
# 数组r 用来存储结果，r[0]表示K 近邻中“0”的个数，r[n]表示K 近邻中“n”的个数
r=np.zeros(10)
for i in temp:
	r[int(i)]+=1
#print(r)
print('当前的数字可能为:'+str(np.argmax(r)))

4. K 近邻模块的基本使用

在 OpenCV 中，不需要自己编写复杂的函数实现K 近邻算法，直接调用其自带的模块函数即可。本节通过一个简单的例子介绍如何使用OpenCV 自带的K 近邻模块。

本例中有两组位于不同位置的用于训练的数据集，如图所示。两组数据集中，一组位于左下角；另一组位于右上角。随机生成一个数值，用OpenCV 中的K 近邻模块判断该随机数属于哪一个分组。

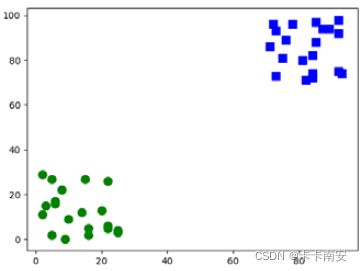
上述两组数据中，位于左下角的一组数据，其x、y 坐标值都在(0, 30)范围内。位于右上角的数据，其x、y 坐标值都在(70, 100)范围内。

根据上述分析，创建两组数据，每组包含20 对随机数（20 个随机数据点）：

rand1 = np.random.randint(0, 30, (20, 2)).astype(np.float32)
rand2 = np.random.randint(70, 100, (20, 2)).astype(np.float32)

• 第 1 组随机数rand1 中，其x、y 坐标值均位于(0, 30)区间内。
• 第 2 组随机数rand2 中，其x、y 坐标值均位于(70, 100)区间内。

接下来，为两组随机数分配标签：

• 将第 1 组随机数对划分为类型0，标签为0。
• 将第 2 组随机数对划分为类型1，标签为1。

然后，生成一对值在(0, 100)内的随机数对：

test = np.random.randint(0, 100, (1, 2)).astype(np.float32)

最后，使用OpenCV 自带的K 近邻模块判断生成的随机数对test 是属于rand1 所在的类型0，还是属于rand2 所在的类型1。

import cv2
import numpy as np
import matplotlib.pyplot as plt
# 用于训练的数据
# rand1 数据位于(0,30)
rand1 = np.random.randint(0, 30, (20, 2)).astype(np.float32)
# rand2 数据位于(70,100)
rand2 = np.random.randint(70, 100, (20, 2)).astype(np.float32)
# 将 rand1 和rand2 拼接为训练数据
trainData = np.vstack((rand1, rand2))

# 数据标签，共两类：0 和1
# r1Label 对应着rand1 的标签，为类型0
r1Label=np.zeros((20,1)).astype(np.float32)
# r2Label 对应着rand2 的标签，为类型1
r2Label=np.ones((20,1)).astype(np.float32)
tdLable = np.vstack((r1Label, r2Label))

# 使用绿色标注类型0
g = trainData[tdLable.ravel() == 0]
plt.scatter(g[:,0], g[:,1], 80, 'g', 'o')
# 使用蓝色标注类型1
b = trainData[tdLable.ravel() == 1]
plt.scatter(b[:,0], b[:,1], 80, 'b', 's')
# plt.show()

# test 为用于测试的随机数，该数在0 到100 之间
test = np.random.randint(0, 100, (1, 2)).astype(np.float32)
plt.scatter(test[:,0], test[:,1], 80, 'r', '*')

# 调用OpenCV 内的K 近邻模块，并进行训练
knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, tdLable)
# 使用K 近邻算法分类
ret, results, neighbours, dist = knn.findNearest(test, 5)
# 显示处理结果
print("当前随机数可以判定为类型：", results)
print("距离当前点最近的5 个邻居是：", neighbours)
print("5 个最近邻居的距离: ", dist)
# 可以观察一下显示，对比上述输出
plt.show()

运行上述程序，显示的运行结果（因为是随机数，每次结果会略有不同）为：

当前随机数可以判定为类型： [[1.]]
距离当前点最近的5 个邻居是： [[1. 1. 1. 1. 1.]]
5 个最近邻居的距离: [[313. 324. 338. 377. 405.]]

同时，程序还会显示如图所示的运行结果。从图中可以看出，随机点（星号点）距离右侧小方块（类型为1）的点更近，因此被判定为属于小方块的类型1。

5. 使用OpenCV进行手写数字识别

本节使用OpenCV 自带的K 近邻模块识别手写数字（效果很差）。

效果好坏完全由喂入K近邻函数的数据集决定。

import cv2
import numpy as np
import matplotlib.pyplot as plt

#读取样本（特征）图像的值
s='image\\'  #图像所在路径
num=100 #共有样本数量
row=240 #每个数字图像的行数
col=240 #每个数字图像的列数
a=np.zeros((num,row,col)) #用来存储所有样本的数值
#print(a.shape)
n=0 #用来存储当前图像的编号。
for i in range(0,10):
    for j in range(1,11):
        a[n,:,:]=cv2.imread(s+str(i)+'\\'+str(i)+'-'+str(j)+'.bmp',0)
        n=n+1

#提取样本图像的特征
feature=np.zeros((num,round(row/5),round(col/5))) #用来存储所有样本的特征值
#print(feature.shape)  #看看feature的shape长什么样子
#print(row)            #看看row的值，有多少个特征（100）个
for ni in range(0,num):
    for nr in range(0,row):
        for nc in range(0,col):
            if a[ni,nr,nc]==255:
                feature[ni,int(nr/5),int(nc/5)]+=1
f=feature   #简化变量名称

#将feature处理为单行形式
train = feature[:,:].reshape(-1,round(row/5)*round(col/5)).astype(np.float32) 
#print(train.shape)

#贴标签，需要注意range(0,100)不是range(0,101)
trainLabels = [int(i/10)  for i in range(0,100)]
trainLabels=np.asarray(trainLabels)
#print(*trainLabels)   #打印测试看看标签值

##读取图像值
o=cv2.imread('image\\test\\5.bmp',0) #读取待测图像
of=np.zeros((round(row/5),round(col/5))) #用来存储测试图像的特征值
for nr in range(0,row):
    for nc in range(0,col):
        if o[nr,nc]==255:
            of[int(nr/5),int(nc/5)]+=1
test=of.reshape(-1,round(row/5)*round(col/5)).astype(np.float32) 

#调用函数识别
knn=cv2.ml.KNearest_create()
knn.train(train,cv2.ml.ROW_SAMPLE, trainLabels)
ret,result,neighbours,dist = knn.findNearest(test,k=5)
cv2.imshow("test",o)
print("当前随机数可以判定为类型：", result)
print("距离当前点最近的5个邻居是：", neighbours)
print("5个最近邻居的距离: ", dist)
cv2.waitKey()
cv2.destroyWindow("test")

运行上述程序，程序运行结果为：

当前随机数可以判定为类型： [[5.]]
距离当前点最近的5 个邻居是： [[5. 3. 5. 3. 5.]]
5 个最近邻居的距离: [[77185. 78375. 79073. 79948. 82151.]]