Python数据结构与算法中的栈详解(3)

目录

• 前序、中序和后序表达式是什么？
• 我们为什么要学习前/后序表达式？
• 从中序向前序和后序转换
• 用Python实现从中序表达式到后序表达式的转换​
• 计算后序表达式
• 总结

前序、中序和后序表达式是什么？

对于像B∗C 这样的算术表达式，可以根据其形式来正确地运算。在B∗C 的例子中，由于乘号出现在两个变量之间，因此我们知道应该用变量 B 乘以变量 C 。​

因为运算符出现在两个操作数的中间 ，所以这种表达式被称作中序表达式 。​

来看另一个中序表达式的例子：A+B∗C。虽然运算符 “ + ” 和 “ * ” 都在操作数之间，但是存在一个问题：它们分别作用于哪些操作数？ “ + ” 是否作用于 A 和 B ？“ * ” 是否作用于 B 和 C ？这个表达式看起来存在歧义。​

事实上，我们经常读写这类表达式，并且没有遇到任何问题。这是因为，我们知道运算符的特点。每一个运算符都有一个优先级 。在运算时，高优先级的运算符先于低优先级的运算符参与运算。唯一能够改变运算顺序的就是括号。乘法和除法的优先级高于加法和减法。​

尽管这些规律对于人来说显而易见，计算机却需要明确地知道以何种顺序进行何种运算。一种杜绝歧义的写法是完全括号表达式 。这种表达式对每一个运算符都添加一对括号。由括号决定运算顺序，没有任何歧义，并且不必记忆任何优先级规则。​

比如，A+B∗C+D可以被重写成((A+(B∗C))+D)， 以表明乘法优先，然后计算左边的加法表达式。由于加法运算从左往右结合，因此A+B+C+D可以被重写成(((A+B)+C)+D)。​

我们已经了解了中序表达式的原理， 还有另外两种重要的表达式，也许并不能一目了然地看出它们的含义，那就是前序和后序表达式。​

以中序表达式A+B为例。如果把运算符放到两个操作数之前，就得到了前序表达式+AB 。同理，如果把运算符移到最后，会得到后序表达式AB+ 。这两种表达式看起来有点奇怪。​

通过改变运算符与操作数的相对位置，我们分别得到 前序表达式 和 后序表达式 。前序表达式要求所有的运算符出现在它所作用的两个操作数之前，后序表达式则相反。下表列出了一些例子。

中序表达式	前序表达式	后序表达式
A + B	+ A B	A B +
A + B * C	+ A * B C	A B C * +

 A+B∗C可以被重写为前序表达式 + A ∗ B C 

乘号出现在 B 和 C 之前，代表着它的优先级高于加号。加号出现在 A 和乘法结果之前。

A+B∗C对应的后序表达式是 A B C ∗ + 

运算顺序仍然得以正确保留，这是由于乘号紧跟 B 和 C 出现，意味着它的优先级比加号更高。

关于前序表达式和后序表达式，尽管运算符被移到了操作数的前面或者后面，但是运算顺序并没有改变。
​

再举一个例子：现在来看看中序表达式  (A+B)∗C。

括号用来保证加号的优先级高于乘号。但是，当A+B被写成前序表达式时，只需将加号移到操作数之前，即+AB。于是，加法结果就成了乘号的第一个操作数。乘号被移到整个表达式的最前面，从而得到∗+ABC。​

同理，后序表达式 A B + A B+ AB+保证优先计算加法。乘法则在得到加法结果之后再计算。因此，正确的后序表达式为 AB+C∗。​

一些中序、前序与后序表达式对应示例：

中序表达式	前序表达式	后序表达式
A + B * C + D	+ + A * B C D	A B C * + D +
(A + B) * (C + D)	* + A B + C D	A B + C D + *
A * B + C * D	+ * A B * C D	A B * C D * +
A + B + C + D	+ + + A B C D	A B + C + D +

我们为什么要学习前/后序表达式？

在上面的中序表达式变为前/后序表达式的例子中，请注意一个非常重要的变化。在后两个表达式中，括号去哪里了？为什么前序表达式和后序表达式不需要括号？答案是，这两种表达式中的运算符所对应的操作数是明确的。只有中序表达式需要额外的符号来消除歧义。前序表达式和后序表达式的运算顺序完全由运算符的位置决定。​

前序表达式是一种十分有用的表达式，它将中序表达式转换为可以依靠简单的操作就能得到运算结果的表达式。例如， ( a + b ) ∗ ( c + d ) (a+b)*(c+d) (a+b)∗(c+d)转换为 ∗ + a b + c d *+ab+cd ∗+ab+cd。它的优势在于只用两种简单的操作，入栈和出栈就可以解决任何中序表达式的运算。——《百度百科关于前序表达式作用的解释》

从中序向前序和后序转换

到目前为止，我们使用了一种难以言明的方法来将中序表达式转换成对应的前序表达式和后序表达式。正如我们所想的那样，这其中一定存在通用的算法，可用于正确转换任意复杂度的表达式。

一个容易观察到的方法是替换括号法，但前提是使用完全括号表达式。

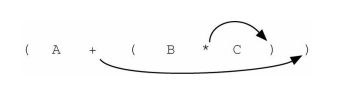
如前所述，可以将A+B∗C写作(A+(B∗C))，以表示乘号的优先级高于加号。进一步观察后会发现，每一对括号其实对应着一个中序表达式（包含两个操作数以及其间的运算符）。 观察子表达式(B∗C)的右括号。如果将乘号移到右括号所在的位置，并且去掉左括号，就会得到BC∗，这实际上是将该子表达式转换成了对应的后序表达式。如果把加号也移到对应的右括号所在的位置，并且去掉对应的左括号，就能得到完整的后序表达式。

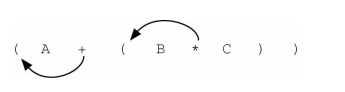
如果将运算符移到左括号所在的位置，并且去掉对应的右括号，就能得到前序表达式，如下图所示。实际上，括号对的位置就是其包含的运算符的最终位置。

因此，若要将任意复杂的中序表达式转换成前序表达式或后序表达式，可以先将其写作完全括号表达式， 然后将括号内的运算符移到 左括号处（前序表达式） 或者 右括号处（后序表达式）。

用Python实现从中序表达式到后序表达式的转换​

我们需要开发一种将任意中序表达式转换成后序表达式的算法。为了完成这个目标，让我们进一步观察转换过程。​

再一次研究A+B∗C这个例子。如前所示，其对应的后序表达式为 ABC∗+。操作数 A 、B 和 C 的相对位置保持不变，只有运算符改变了位置。再观察中序表达式中的运算符。从左往右看，第一个出现的运算符是 + 。但是在后序表达式中，由于 * 的优先级更高（写成完全括号表达式后乘法所在的括号先进行运算），因此 * 先于 + 出现。在本例中，中序表达式的运算符顺序与后序表达式的相反。​

在转换过程中，由于运算符右边的操作数还未出现（不知道运算符右边是否还有括号运算）， 因此需要先将运算符保存在某处。同时，由于运算符有不同的优先级，因此可能需要反转它们的保存顺序。 本例中的加号与乘号就是这种情况。由于中序表达式中的加号先于乘号出现，但乘号的运算优先级更高，因此后序表达式需要反转它们的出现顺序。鉴于这种反转特性，使用栈来保存运算符就显得十分合理。​

那么对于(A+B)∗C，情况会如何呢？它对应的后序表达式为 AB+C∗。从左往右看，首先出现的运算符是 + 。不过，由于括号改变了运算符的优先级，因此当处理到 * 时，+ 已经被放入结果表达式中了。​

现在可以来总结转换算法： 当遇到左括号时，需要将左括号保存下来，以表示接下来的内容里会遇到高优先级的运算符（就算括号里出现的运算符本身的优先级低，但也因为在括号里而优先级高了起来）；那个运算符需要等到左括号对应的右括号出现，才能确定转换为后序表达式之后它应该存在的位置 （回忆一下完全括号表达式的转换法）；当右括号出现时，也就是确定了括号内运算符在后序表达式中的存在位置，便可以将左括号和左括号上面的其他运算符（可能有可能没有）从栈中取出来。 (用于完全括号表达式)​

用代码实现转换算法：

​假设中序表达式是一个以空格分隔的标记串。其中， 运算符标记有+−∗/ ，括号标记有“ ( ( (”和“ ) ) )” ，操作数标记有 A 、B 、C 等。下面的步骤会生成一个后序标记串。​

步骤：

1.创建用于保存运算符的空栈 opstack ，以及一个用于保存结果的空列表。

2.使用字符串方法 split 将输入的中序表达式转换成一个列表。

3.从左往右扫描这个标记列表

3.1 如果标记是操作数，将其添加到结果列表的末尾。

3.2 如果标记是左括号，将其压入 opstack 栈中。

3.3 如果标记是右括号，反复从 opstack 栈中移除元素，直到移除对应的左括号。将从栈中取出的每 一个运算符都添加到结果列表的末尾。

3.4 如果标记是运算符，将其压入 opstack 栈中。但是，在这之前，需要先从栈中取出优先级更高或相同的运算符，并将它们添加到结果列表的末尾。

4.当处理完输入表达式以后，检查 opstack 栈。将其中所有残留的运算符全部添加到结果列表的末尾。​

为了在Python中实现这一算法，我们使用一个叫作 prec 的字典来保存运算符的优先级值。该字典把每一个运算符都映射成一个整数。通过比较对应的整数，可以确定运算符的优先级（本例随意地使用了3、2、1）。左括号的优先级值最小。这样一来，任何与左括号比较的运算符都会被压入栈中。我们也将导入string 模块，它包含一系列预定义变量。本例使用一个包含所有大写字母的字符（string.ascii_uppercase ）来代表所有可能出现的操作数。下述代码展示了完整的转换过程。

import string
class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def pop(self):
        return self.items.pop()
    def push(self, item):
        self.items.append(item)
    def peek(self):
        return self.items[len(self.items) - 1]
def infixToPostfix(infixexpr):
    prec = {
        "*" : 3,
        "/" : 3,
        "+" : 2,
        "-" : 2,
        "(" : 1
        }
    opStack = Stack()  # 创建栈
    postfixList = []  # 创建结果列表
    tokenList = infixexpr.split()  # 分割算式为列表
    for token in tokenList:                   # 遍历算式
        if token in string.ascii_uppercase:   # 如果当前元素是操作数
            postfixList.append(token)         # 直接放入结果列表
        elif token == "(":                    # 如果当前元素是 左括号
            opStack.push(token)               # 左括号入栈
        elif token == ")":                    # 如果当前元素是 右括号
            topToken = opStack.pop()          # 从栈中取元素
            while topToken != "(":            # 取到的元素 不是右括号 循环执行
                postfixList.append(topToken)  # 元素放入结果列表
                topToken = opStack.pop()      # 从栈中取元素
        else:                                 # 遍历到的元素是 运算符
            while (not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]):
                # （栈非空）并且（栈顶的运算符优先级大于等于当前运算符优先级）循环执行：
                #  栈顶元素入结果列表
                postfixList.append(opStack.pop())
            # 运算符入栈
            opStack.push(token)
    # 把栈里剩下的运算符全放入结果列表
    while not opStack.isEmpty():
        postfixList.append(opStack.pop())
    # 返回拼接后的后序表达式字符串
    return " ".join(postfixList)
print(infixToPostfix("A + B * C"))
# A B C * +
print(infixToPostfix("( A + B ) * ( C + D )"))
# A B + C D + *

计算后序表达式

最后一个关于栈的例子是计算后序表达式。在这个例子中，栈再一次成为适合选择的数据结构。不过，当扫描后序表达式时，需要保存的是操作数，而不是运算符。换一个角度来说，当遇到一个运算符时，需要用离它最近的两个操作数来计算。​

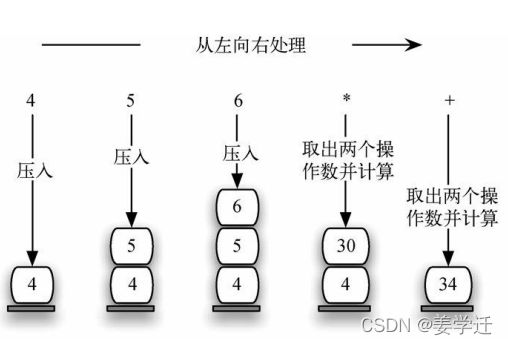
为了进一步理解该算法，考虑后序表达式 4 5 6 * + 。当从左往右扫描该表达式时，首先会遇到操作数 4 和 5 。在遇到下一个符号之前，我们并不确定要对它们进行什么运算。故而将它们都保存在栈中，便可以在需要时取用。​

在本例中，紧接着 4 和 5 后出现的符号又是一个操作数。因此，将 6 也压入栈中，并继续检查后面的符号。​

现在遇到了运算符 * ，这意味着需要将最近遇到的两个操作数相乘。通过执行两次出栈操作，可以得到相应的操作数，然后进行乘法运算 5 ∗ 6 5*6 5∗6（本例的结果是30）。​

接着，将结果压入栈中。这样一来，当遇到后面的运算符时，它就可以作为操作数。当处理完最后一个运算符之后，栈中就只剩一个值。然后就可以将这个值取出来，并作为表达式的结果返回。​

过程如图所示：

需要特别注意的是：​

处理除法运算时需要非常小心。由于后序表达式只改变运算符的位置，因此操作数的位置与在中序表达式中的位置相同。当从栈中依次取出除号的操作数时，它们的顺序是颠倒的，因此我们要必须保证操作数的顺序不能颠倒。​

用代码实现后序表达式计算过程：​

假设后序表达式是一个以空格分隔的标记串。其中， 运算符标记有 ∗ / + − * / + - ∗/+−，操作数标记是一位的整数值。结果是一个整数。​

步骤：

1.创建空栈 operandStack

2.使用字符串方法 split 将输入的后序表达式转换成一个列表

3.从左往右扫描这个标记列表：

(1) 如果标记是操作数，将其转换成整数(因为当前是字符)并且压入 operandStack 栈中

(2) 如果标记是运算符，从 operandStack 栈中取出两个操作数。第一次取出右操作数，第二次取出左操作数。进行相应的算术运算，然后将运算结果压入 operandStack 栈中。

4.当处理完输入表达式时，栈中的值就是结果。将其从栈中返回。​

为了方便运算，我们定义了辅助函数 doMath 。它接受一个运算符和两个操作数，并进行相应的运算。

import string

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def pop(self):
        return self.items.pop()
    def push(self, item):
        self.items.append(item)
    def peek(self):
        return self.items[len(self.items) - 1]

def postfixEval(postfixExpr):
    operandStack = Stack()                             # 创建存放元素的栈
    tokenList = postfixExpr.split()                    # 分割算式字符串
    for token in tokenList:                            # 遍历算式元素
        if token in "0123456789":                      # 如果 元素 是 操作数
            operandStack.push(int(token))              # 转化为整型 入栈
        else:                                          # 元素不是操作数 是运算符
            operand2 = operandStack.pop()              # 从栈顶取 操作数2
            operand1 = operandStack.pop()              # 从栈顶取 操作数1
            result = doMath(token,operand1,operand2)   # 调用doMath进行运算
            operandStack.push(result)                  # 运算结果 入栈
    return operandStack.pop()                          
    # 返回栈内元素（遍历结束后这个唯一的元素就是整个算式的结果）
def doMath(op,op1,op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注脚本之家的更多内容!