强化学习15——Proximal Policy Optimization (PPO)算法详细推导

在Policy Gradient推导和REINFORCE算法两篇文章介绍了PG算法的推导和实现，本篇要介绍的算法是Proximal Policy Optimization (PPO)，中文叫近短策略优化算法。PPO由于其非常的好的性能与易于实现等特性，已被作为OpenAI公司的首选算法，可见这个算法的优秀性能，具体可以查看OpenAI-PPO

一、Policy Gradient 的不足

• 采样效率低下：PG采用MC采样方式，每次基于当前的策略对环境采样一个episode数据，然后基于这些数据更新策略，这个过程中数据仅仅被利用了一次就扔掉了，相比于DQN等离线学习算法，PG这种更新方式是对数据的极大浪费。
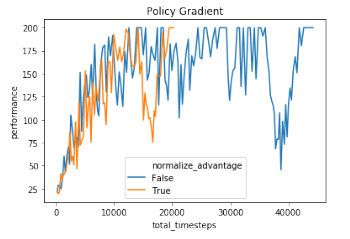
• 训练不稳定：在强化学习中当前的动作选择会影响到将来的情况，不像监督学习的训练样本是相互独立的，如果某一批次的样本不好导致模型训练的很差，只要其他的训练数据没问题最终也能得到一个好的结果。但是在PG中，对于某次策略更新的太大或者太小，就会得到一个不好的Policy，一个不好的和环境交互就会得到一个不好的数据，用这些不好的数据更新的策略很大概率也是不好的。所以训练时候会有下图这种情况，训练过程中会忽然进入一个很差的状态。

在TRPO算法中，对于第一个问题可以使用importance sampling的方式，第二个问题使用Trust region and natural policy gradient方法，TRPO算法是OpenAI在15年提出的算法，做了很多开创性的工作，当然要理解起来论文也不是那么容易的，PPO可以看作是TRPO的一个简化版本，也用到了importance sampling技术，然后效果也不输TRPO，感兴趣的可以自行阅读Arxiv: TRPO

二、重要性采样

重要性采样(importance sampling)是一种近似的采样方法，如下式子所示：我们要求f(x)的期望，其中x服从p(x)分布，可以通过如下入学变换，x可以从另外一个分布q(x)中采样，这时f(x)就需要乘上一个重要性权重$\frac{p(x)}{q(x)}$. 通过这种方式就可以从另外一个分布采样来计算原式，后面只需要乘上一个重要性权重就可以了。

那么重要性权重有什么用呢？上面说了PG算法效率低下，是因为PG属于on-policy算法，那我们能不能把PG变成off-policy算法呢？答案是可以的，方法就是重要性采样。

PG的策略更新梯度为：$\nabla J(\theta )=E_{\tau -p_{\theta }(\tau )}[R(\tau )\nabla log{p}_{\theta }(\tau )]$ ，根据上面的式子，更新梯度可以变为如下形式：
$$\nabla J(\theta )=E_{\tau -p_{{\theta }^{\prime }}(\tau )}\left[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}R(\tau )\nabla log{p}_{\theta }(\tau )\right]$$
此时有两个策略，参数分别为 ${\theta }^{\prime }$和$\theta$ ，我们使用${\theta }^{\prime }$ 来和环境交互采样数据，然后用来更新 $\theta$ 策略，这样就变成了off-policy 方式，采集到的数据可以进行多次更新。$\theta$ 更新多次之后把参数复制给 ${\theta }^{\prime }$ .

下面把使用优势函数的形式改成off-policy形式：

使用优势函数的更新梯度为：
$$E_{(s_t,a_t)-{\pi }_{\theta }}[A^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]$$
使用重要性采样后有：
$$\begin{array}{rl}=& E_{(s_t,a_t)-{\pi }_{{\theta }^{\prime }}}\left[\frac{P_{\theta }(s_t,a_t)}{P_{{\theta }^{\prime }}(s_t,a_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)\right]\\ =& E_{(s_t,a_t)-{\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}\frac{p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)\right]\end{array}$$
上式中需要注意的第一点是对于优势函数的计算，$A^{\theta }(s_t,a_t)$要变为$A^{{\theta }^{\prime }}(s_t,a_t)$。因为优势函数是基于采样策略的和环境交互的数据计算的，这里我们的采样策略参数是${\theta }^{\prime }$，所以要换成 ${\theta }^{\prime }$。另外一点是对于 $\frac{p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(s_t)}$ 一般认为分子分母是近似相等的，这么处理的原因1是对于$p_{\theta }(s_t)$ 难以计算（比如游戏中某一状态的概率怎么算？）第二点就是在PPO中我们要求策略 $\theta$ 和${\theta }^{\prime }$ 差别不能太大，这样就算计算出来 $p_{\theta }(s_t)$ 和 $p_{{\theta }^{\prime }}(s_t)$, 最终结果也会接近于1。至于为什么两个分布不能差别太大，下面会具体介绍。到这里我们就得到了优势函数形式PPO损失函数：
$$J^{{\theta }^{\prime }}(\theta )=E_{(s_t,a_t)-{\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\right]$$
其中$J^{{\theta }^{\prime }}(\theta )$ 表示用 ${\theta }^{\prime }$ 采样，用$\theta$ 更新。

三、梯度更新约束问题

上面我们说了，在PPO算法中这两个分布不能相差太远，下面来解释原因。还是回到下面这个重要性采样例子：
$$E_{x-p}[f(x)]=E_{x-q}[\frac{p(x)}{q(x)}f(s)]$$
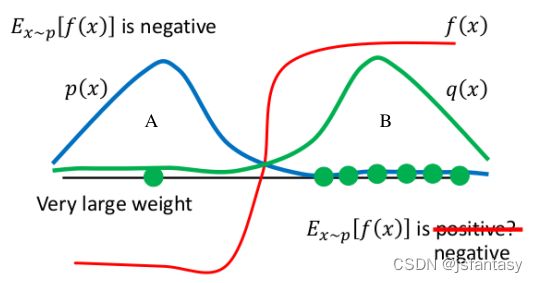
**上面这个公式在理论上是没有问题的，即便p 分布和q分布差别很大也没问题，前提是需要非常大量的采样。但是在实际算法中，由于做不到非常大量的采样，所以这里需要给p分布和q分布加一个限制，就是不能差别太大。**下面结合图片讲解，如图红线代表f(x)，蓝色线为p(x)分布，绿色线为 q(x)分布，其分布差别很大。

• 如果不采用重要性采样方法的话，直接从p(x)分布采样有限的一些点，那么很大概率上会采样到A区域，那么此时算出来f(x)的期望是负的。
• 如果我们在 q(x)分布采样的话，很大概率会采样带范围B（采样点为右边六个绿色点），那么此时很容易会得出 E[f(x)] 是正数的情况。但实际上根据p(x)分布可以看出在采样有限点下 f(x) 的期望应该是负的，这显然是有问题的。
• 如果再继续采样一个点（假如最左边的一个点），这个点在 q 分布下被采样到的几率很小，所以要大量采样，在这个点下计算 $\frac{p(x)}{q(x)}$会得到一个非常大的数，最后的结果f(x)的期望仍然是负数。
• 也就是说尽管在 q 分布下采样到的点很容易都在 B 区域，但是这里的点的 重要性权重 $\frac{p(x)}{q(x)}$ 很小，虽然采样到B区域以外的点概率很小，但是重要性权重比较高。这也是对乘上 $\frac{p(x)}{q(x)}$ 直观的理解。但是这需要大量采样，在算法中采样数量不多时候是不成立的，所以需要对p分布和q分布做一个限制：不能相差太大。

下面谈谈PPO中的限制，PPO论文提供了两种限制梯度更新方式：

• PPO1

PPO1使用KL距离来表示两个分布的差距大小，并把KL距离作为一个惩罚项，使用参数$\beta$来调节

• 如果KL距离太大了，说明没有起到惩罚的作用，需要增加$\beta$
• 如果KL距离太小了，说明惩罚的太严重了，此时适当的减小 $\beta$ 的值

• PPO2

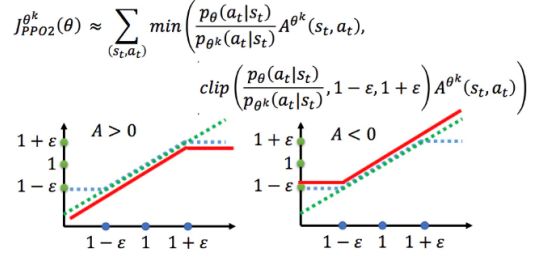
PPO2没有使用 KL 距离限制，而是直接用 clip 剪切。把重要性权重限制在 $(1-ϵ,1+ϵ)$ 范围内。

• 当优势函数 A > 0时，要增加某些动作出现的概率，限制重要性权重，使得梯度不要增加的太快
• 当优势函数 A < 0时，要减小某些动作出现的概率，限制重要性权重，使得梯度不要减小的太快

具体可以结合着图片个式子分析下。这种处理法方法简单粗暴，但效果却出奇的好，不得不说真的很神奇。

以上就是PPO理论部分的内容了，代码实现连接见PPO TF2.X实现，对比着PG的代码和上述理论知识，还是挺好理解的。本篇文章部分图片参考了李宏毅老师的课件，另外李宏毅老师讲的真的不错，简单易懂，这里放上课程链接：李宏毅强化学习。
另外，本强化学习算法系列尤其是头几篇文章参考了周博磊老师的强化学习纲要，周老师的课程更加偏理论一些，对初学者可能不太友好，建议先对算法有个直观的了解然后再观看。

强化学习常用算法打算就介绍这么多，后面会更新一些模仿学习和多智能体强化学习的内容