建立一颗最优的决策树 -如何调参,根据决策树进行数据分析
此篇文章主要介绍了如何获得一颗最优的决策树
关键思想:要构建一棵完美的树,你需要在信息量最大的特征处拆分树,从而得到最纯的子节点
criterion=‘gini’:基尼不纯度是一种误分类的度量,目标是最小化误分类的概率。数据的完美拆分(每个子组包含一个目标标签的数据点)产生的基尼系数为0。我们可以度量树的每种可能拆分的基尼系数,然后选择基尼不纯度最低的那个。它常用于分类和回归树.
criterion=‘entropy’(也称为信息增益):在信息论中,熵是与信号或者分布相关的不确定量的度量。一个完美的数据拆分熵为0。我们可以度量树的每种可能拆分的熵,然后选择熵最低的那个.
关于决策树:
优点
天然的可解释性。 这是决策树最大的优点了,常用于医学等需要可解释性强的分类器
可以处理缺失值(missing), 字符型(nominal), 数值型(numeric)等数据类型。
非参数模型(non-parametric)。 没有复杂的参数设置,谁跑效果都相对一样。
运算速度相对比较快.
缺点
最大的缺点就是很容易过拟合。 导致实际预测的效果并不高。
不适合处理高维数据, 当属性数量过大的时候,决策树相当复杂
对异常值(Outlier)过于敏感, 很容易导致树的结构的巨大的变换。
泛化(Generalization)能力太差, 对于没有出现过的值几乎没有办法分类,鲁棒性差
控制决策树的复杂度
你继续生成一棵树,直到所有的叶子节点都是纯的,那么通常你会得到一棵过于复杂且无法解释的树
纯叶子节点的出现意味着这棵树是100%正确的,也就是过拟合le
决策树避免过拟合有两种常见的方法:
1.先减枝,也就是提前停止树的创建过程
2.后减枝,也就是树形成后再删除或者折叠包含少量信息的节点
1.先减枝:DecisionTreeclassifier
传入参数.
1.max_depth 限制树的最大深度
2.max_leaf_nodes 限制叶子节点的最大数量
3.min_samples_splits 继续拆分节点所需要的节点中最少点数
项目实战:使用决策树诊断乳腺癌
乳腺癌Wisconsin数据集
https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+ (Diagnostic)
sklearn 中 load_breast_cancer
'''初始化与数据集加载'''
from sklearn import datasets
from sklearn import tree
import sklearn.model_selection
import numpy as np
import matplotlib.pyplot as plt
# breast_cancer.data.shape #(569, 30) 569张图的30个特征
# breast_cancer.feature_names.shape #(30,) 30个特征
breast_cancer= datasets.load_breast_cancer()
feature_names = breast_cancer.feature_names
target,Data = breast_cancer.target,breast_cancer.data
target_names = breast_cancer.target_names
dir(breast_cancer)
['DESCR',
'data',
'feature_names',
'filename',
'frame',
'target',
'target_names']
xTrain,xTest,yTrain,yTest = sklearn.model_selection.train_test_split(Data,target,test_size=0.1,random_state=7)
cancer_dtree = tree.DecisionTreeClassifier()
cancer_dtree.fit(xTrain,yTrain)
with open('Dot/cancer_dtree1.dot','w') as f:
tree.export_graphviz(cancer_dtree,f,feature_names = feature_names,class_names = target_names)
这棵树的特征分布不平衡,balance tree,左子树深度为7,右子树为5,如下图
目前问题如下:
非对称树意味着什么?
树的深度可能导致过拟合,对于两个相同性能的树,我们偏向于depth小的
决策树只不过是在不同的特征上执行一组分层逻辑运算,以产生一个预测
print(cancer_dtree.score(xTest,yTest))
0.9473684210526315
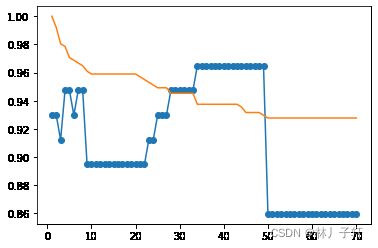
'''探索 树的深度 对于性能的影响'''
max_depths = np.arange(1,71,1)
train_score = []
test_score = []
for index,data in enumerate(max_depths):
dtree = tree.DecisionTreeClassifier(max_depth=data)
dtree.fit(xTrain,yTrain)
train_score.append(dtree.score(xTrain,yTrain))
test_score.append(dtree.score(xTest,yTest))
plt.plot(max_depths,test_score,'o-',label ='test' )
plt.plot(max_depths,train_score,label ='train' )
plt.scatter(max_depths,test_score)
plt.xlabel('tree depth')
plt.ylabel('accuracy score')
plt.show()
从结果上看似乎树越深,模型的效果越好
但是,树的深度可能导致过拟合,对于两个相同性能的树,我们偏向于depth小的
depth 取 17
'''探索 限制叶子节点的容量最小值 对性能的影响'''
min_samples = np.arange(1,71,1) #min_samples_leaf
train_score1 = []
test_score1 = []
for index,data in enumerate(min_samples):
dtree = tree.DecisionTreeClassifier(min_samples_leaf = data)
dtree.fit(xTrain,yTrain)
train_score1.append(dtree.score(xTrain,yTrain))
test_score1.append(dtree.score(xTest,yTest))
plt.plot(min_samples,test_score1,label ='test' )
plt.plot(min_samples,train_score1,label ='train' )
plt.scatter(min_samples,test_score1)
plt.show()
从上图中我们可以看到,min_samples_leaf限制在 40左右会有最优值
'''得出我们的最优参数模型
max_depth = 17
min_samples_leaf = 40'''
dtree_best = tree.DecisionTreeClassifier(min_samples_leaf=40,max_depth=17)
dtree_best.fit(xTrain,yTrain)
dtree_best.score(xTest,yTest)
with open('Dot/bestDot/best_cancer_dtree.dot','w') as f:
tree.export_graphviz(dtree_best,f,feature_names = feature_names,class_names = target_names)
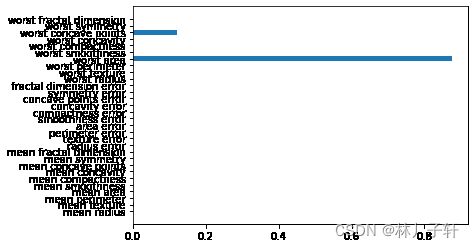
'''最重要的特征'''
dtree_best_importance = dtree_best.feature_importances_
plt.barh(range(len(feature_names)),dtree_best_importance,tick_label = feature_names)
plt.show()
从上图可以看到,乳腺癌 良性或者恶性最根本的判别特征是 worst area 和worst concave points。
最后是生成的最优决策树模型的整体形式(采用的Gini方法)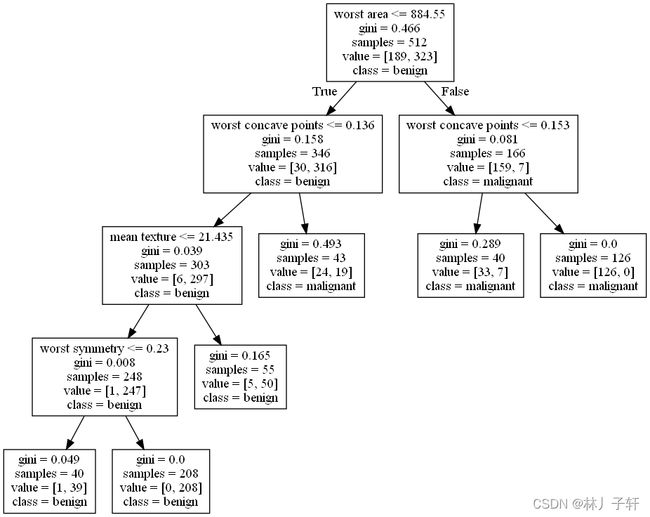
其他文章
决策树的实现与可视化
决策树初探 - 建立一颗简单的决策树
主成分分析,独立成分分析,+t-SNE 分布随机可视化降维的对比
线性回归预测波士顿房价
基于逻辑回归的鸢尾花分类
数据表示和特征工程
参考文献
机器学习 使用OpenCV、Python和scikit-learn进行智能图像处理(原书第2版)-(elib.cc) by (印)阿迪蒂亚·夏尔马(Aditya Sharma)(印)维什韦什·拉维·什里马利(Vishwesh Ravi Shrimali)(美)迈克尔·贝耶勒(Michael Beyeler)
决策树的性质
信息增益