简介
看到文章标题,很多同学可能会疑惑,实现元素的旋转,只需要求得旋转角度,然后用CSS中的transform:rotate(${旋转的角度}deg)就可以实现旋转的需求,为什么要用到线性代数的知识?
我觉得用线性代数的知识实现元素拖拽旋转的理由如下:
- 矩阵中可以同时包含旋转、缩放、平移等信息,不需要进行冗余的计算和属性更新;
- 更加通用。
线性代数的知识作为一种数学知识,是抽象的、通用的,很多GUI编程技术都提供了线性代数矩阵实现元素旋转、缩放、平移等效果,例如CSS中transform属性的matrix(),Canvas中提供的setTransform()等API,安卓Canvas类提供的setMatrix()方法。学会线性代数矩阵旋转,就可以在各个GUI编程技术中通吃此类需求。
拖拽旋转的原理分析
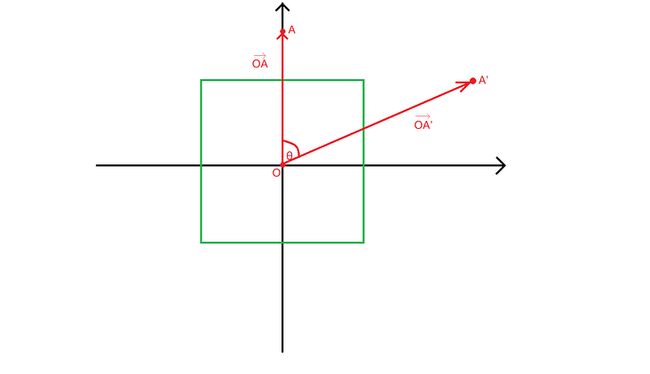
拖拽旋转本质上是绕着原点旋转,这个原点就是物体的中心。让我们用一个矩形来抽象表达这个旋转过程,以矩形中心为原点\(O\),建立\(2D\)坐标系,取一点为旋转起始点\(A\),取一点为旋转结束点\(A'\),将\(A\)、\(A'\)与\(O\)连接起来可得向量\(\overrightarrow{OA}\)、向量\(\overrightarrow{OA'}\),向量\(\overrightarrow{OA}\)和向量\(\overrightarrow{OA'}\)之间的夹角\(\theta\),可得如下图:
在JavaScript中Math.atan2()API可以返回从\(原点(0,0)\)到\((x,y)点\)的线段与\(x轴\)正方向之间的平面角度(弧度值),所以可得求取两个向量之间的夹角弧度的代码如下:
/**
* 计算向量夹角,单位是弧度
* @param {Array.<2>} av
* @param {Array.<2>} bv
* @returns {number}
*/
function computedIncludedAngle(av, bv) {
return Math.atan2(av[1], av[0]) - Math.atan2(bv[1], bv[0]);
}旋转矩阵
在前文线性代数在前端中的应用(一):实现鼠标滚轮缩放元素、Canvas图片和拖拽中,我们知道了缩放元素可以利用缩放矩阵,那么旋转元素也可以利用旋转矩阵,那么怎么推导出旋转矩阵就成了关键。由于我们目前只关心平面维度上的旋转,所以只需要求得\(2D\)维度中的旋转矩阵即可。
假设在\(2D\)坐标轴中有和\(X轴\)、\(Y轴\)分别平行的基向量\(p\)和基向量\(q\),它们之间的夹角为\(90^{\circ}\),将基向量\(p\)和基向量\(q\)同时旋转\(\theta度\),可以得到基向量\(p'\)和基向量\(q'\),根据\(三角函数\)即可以推导出\(p\)、\(p'\)的值。
利用基向量构造矩阵,\(2D\)旋转矩阵就如下:
$$ R(\theta)=\left[ \begin{matrix} p^{'} \\ q^{'} \\ \end{matrix} \right]=\left[ \begin{matrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{matrix} \right] $$
转化为\(4\times4齐次矩阵\)则为:
$$ R(\theta)=\left[ \begin{matrix} p^{'} \\ q^{'} \\ r^{'}\\ w^{'} \\ \end{matrix} \right]=\left[ \begin{matrix} cos\theta & sin\theta & 0 & 0 \\ -sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] $$
CSS中实现矩阵变化的matrix()函数
CSS函数matrix()指定了一个由指定的 6 个值组成的 2D 变换矩阵。matrix(a, b, c, d, tx, ty)是matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1)的简写。
这些值表示以下函数:
matrix( scaleX(), skewY(), skewX(), scaleY(), translateX(), translateY() )例如我们要一个div元素放大两倍,水平向右平移100px,垂直向下平移200px,可以把CSS写成:
div {
transform:matrix(2, 0, 0, 2, 100, 200);
}由于我们采用的是\(4\times4齐次矩阵\)进行矩阵变换计算,所以采用\(RP^{3}下的齐次坐标\)。值得注意的是,关于\(齐次坐标\)我们还可以写成下面这种形式,本文我们将采用这种形式:
$$ \left[ \begin{matrix} a & c & 0 & 0 \\ b & d & 0 & 0 \\ 0 & 0 & 1 & 0 \\ tx & ty & 0 & 1 \end{matrix} \right] $$
矩阵计算库gl-matrix
gl-matrix是一个用JavaScript语言编写的开源矩阵计算库。我们可以利用这个库提供的矩阵之间的运算功能,来简化、加速我们的开发。为了避免降低复杂度,后文采用原生ES6的语法,采用