【机器学习】01 梯度下降(详细注释+动态训练效果图)
前言
让我们把时间的齿轮拨回到20万年前,那时候我们的老祖宗正在那智人没有称霸的地球上每天担惊受怕地生活着。
早期智人什么都吃,蘑菇是他们很喜欢的一种食物,但众所周知有很多蘑菇是有毒的,那我们的祖先是如何判断蘑菇是否有毒呢,如果把一个初级的人工智能穿越回20万年前,它将如何帮助我们的祖先辨别什么样的蘑菇是毒蘑菇,说不定多鉴别出一个毒蘑菇,信息革命也就更早发生,现在大家也就不用在csdn上看文章而可以直接像《黑客帝国》一样读取人工智能技能包了~
理论部分
闲言少叙,书归正文。
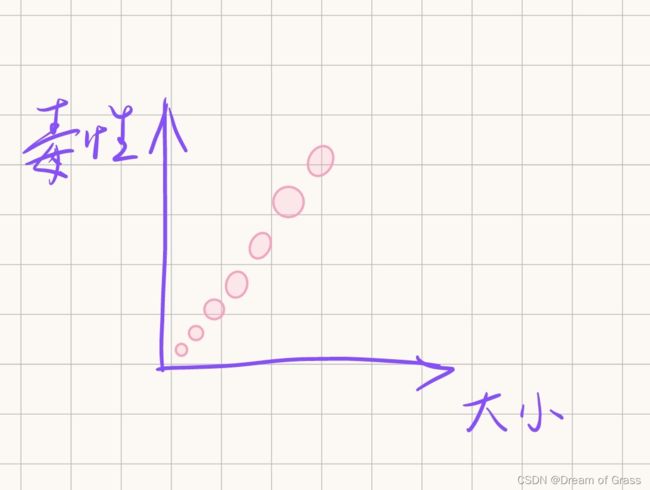
我们先简单假设蘑菇的大小和毒性成正比例关系。
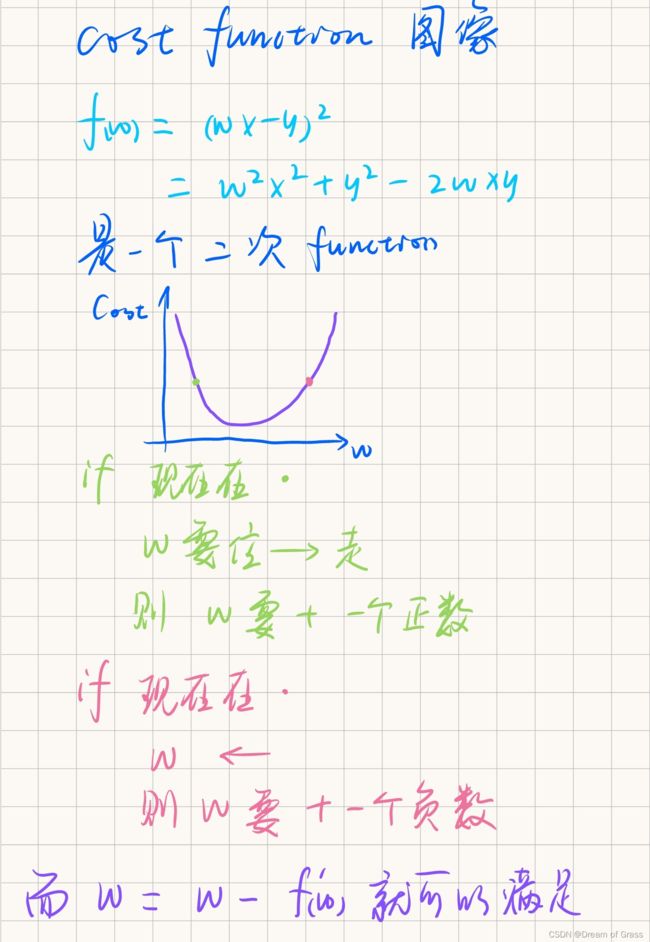
如何衡量预测的毒性和真实的毒性之间的误差呢,我们就通过下图的代价函数来衡量,然后为了使得预测准确,也就是要找到相应的参数,使得代价函数达到最小值。
我们就通过梯度下降算法来找到代价函数的最小值点。
代码部分
生成数据集
建一个dataset.py文件
import numpy as np
def get_mushroom(counts):
xs = np.random.rand(counts)
# 生成counts个x
xs = np.sort(xs)
# 将x们按顺序排列
ys = np.array([1.2*x+np.random.rand()/10 for x in xs])
# 按照y=1.2x生成y,并加入一些小偏差
return xs,ys
导入包和数据集
import numpy as np
from matplotlib import pyplot as plt
import dataset
beans_num = 100
xs, ys = dataset.get_mushroom(beans_num)
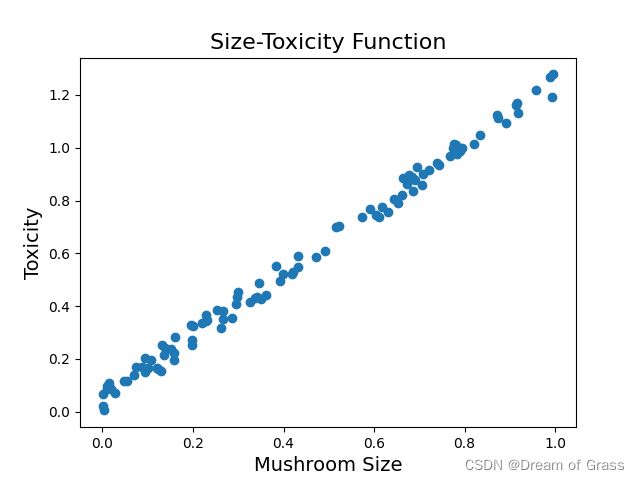
画个散点图
# 画一个散点图,看看豆豆的大小和毒性大致是一个什么关系
plt.scatter(xs, ys)
# 画个标题和横纵坐标
plt.title("Size-Toxicity Function", fontsize=16)
plt.xlabel("Mushroom Size", fontsize=14)
plt.ylabel("Toxicity", fontsize=14)
plt.show()
随机梯度下降
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。(批量梯度下降后面会介绍)
先随便给出一个预测函数,然后通过随机梯度下降来调整参数,具体过程通过画一个动态的图来直观地显示出来。
# 随便给出一个预测函数
w = 0.8
y_pre = w * xs
# print(y_pre)
plt.plot(xs, y_pre, color='green')
# plt.show()
# 上面还是错的离谱,下面使用梯度下降算法来修正w
# 普通随机下降
for _ in range(1):
for i in range(beans_num):
x = xs[i]
y = ys[i]
# 斜率为代价函数对参数求导得来的
k = 2 * (x ** 2) * w -2 * x * y
alpha = 0.1
# 学习率
w = w - alpha * k
# 下面是利用 matplotlib 来画一个动态图,画出参数不断调整的过程
plt.clf()
# 清空窗口
plt.scatter(xs, ys,color='moccasin')
y_pre = w * xs
# print(y_pre)
plt.plot(xs, y_pre, color='crimson')
es = (ys - y_pre) ** 2
avg_e = np.sum(es) / beans_num
plt.xlim(0,1)
plt.ylim(0,1.2)
plt.text(0.02, 1, "误差:",color="mediumturquoise",font='STSong',fontsize=14)
plt.text(0.1, 1, avg_e,color="mediumblue",font='STSong',fontsize=15)
plt.text(0.03,1.13,"w:",color="teal",font='STSong',fontsize=14)
plt.text(0.1,1.13,w,color="teal",font='STSong',fontsize=14)
plt.pause(0.01)
plt.show()
下面就是动态演示效果
批量梯度下降
批量梯度下降法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。
for i in range(beans_num):
# x = xs[i]
# y = ys[i]
# 斜率k=2aw+b
k = 2 * np.sum(xs ** 2) * w + np.sum(-2 * xs * ys)
k=k/100
alpha = 0.1
w = w - alpha * k
plt.clf()
# 清空窗口
plt.scatter(xs, ys, color='moccasin')
y_pre = w * xs
# print(y_pre)
plt.plot(xs, y_pre, color='crimson')
es = (ys - y_pre) ** 2
avg_e = np.sum(es) / beans_num
plt.xlim(0, 1)
plt.ylim(0, 1.2)
plt.text(0.02, 1, "误差:", color="mediumturquoise", font='STSong', fontsize=14)
plt.text(0.1, 1, avg_e, color="mediumblue", font='STSong', fontsize=15)
plt.text(0.03, 1.13, "w:", color="teal", font='STSong', fontsize=14)
plt.text(0.1, 1.13, w, color="teal", font='STSong', fontsize=14)
plt.pause(0.01)
plt.show()
固定步长下降
顾名思义就是按照一定的步长去调整参数,而不是随梯度而去调整步长。
for i in range(beans_num):
# x = xs[i]
# y = ys[i]
# 斜率k=2aw+b
k = 2 * np.sum(xs ** 2) * w + np.sum(-2 * xs * ys)
k=k/100
# alpha = 0.1
step=0.01
# w = w - alpha * k
if k>0:
w=w-step
else:
w+=step
plt.clf()
# 清空窗口
plt.scatter(xs, ys, color='moccasin')
y_pre = w * xs
# print(y_pre)
plt.plot(xs, y_pre, color='crimson')
es = (ys - y_pre) ** 2
avg_e = np.sum(es) / beans_num
plt.xlim(0, 1)
plt.ylim(0, 1.2)
plt.text(0.02, 1, "误差:", color="mediumturquoise", font='STSong', fontsize=14)
plt.text(0.1, 1, avg_e, color="mediumblue", font='STSong', fontsize=15)
plt.text(0.03, 1.13, "w:", color="teal", font='STSong', fontsize=14)
plt.text(0.1, 1.13, w, color="teal", font='STSong', fontsize=14)
plt.pause(0.01)
plt.show()
结语
认为毒性和蘑菇大小成正比例关系的假设实在是太过简单了,后面就用更复杂的假设吧!