R语言——基于主成分分析的自杀影响因素降维
基于主成分分析的自杀影响因素降维
- 一、实验目的
- 二、实验原理
-
- (一)主成分分析
-
- 1.基本原理
- 2.计算步骤
- 三、使用仪器、材料
- 四、实验步骤
- 五、实验过程、结果及分析
-
- (一)数据说明
- (二)数据预处理
-
- 1.缺失值处理
- 2.数据标准化处理
- 3.定类变量哑编码
- (三)主成分分析
-
- 1.计算样本相关系数矩阵
- 2.确定主成分个数及表达式
- 3.主成分解释
- 4.样本回代预测
- 六、参考资料
- 七、附录
这是本人多元统计分析以主成分分析为主题的课程作业,在主成分的解释概括存在一些不足,欢迎交流指正。数据集来源:https://www.kaggle.com/szamil/who-suicide-statistics
一、实验目的
基于主成分分析对WHO公布的1978-2016年自杀率的8个影响因素进行降维处理得到累积贡献率>80%的X个主成分,根据主成分碎石图、散点图和式子对各个主成分进行统计意义解释。
二、实验原理
(一)主成分分析
1.基本原理
主成分分析法是一种降维的统计方法,它借助于一个正交变换,将其分量相关的原随机向量转化成其分量不相关的新随机向量,这在代数上表现为将原随机向量的协方差阵变换成对角形阵,在几何上表现为将原坐标系变换成新的正交坐标系,使之指向样本点散布最开的p 个正交方向,然后对多维变量系统进行降维处理,使之能以一个较高的精度转换成低维变量系统。
2.计算步骤
1)设原始变量X1,X2…Xp的n次观测数据矩阵为:

2)将数据矩阵按列进行中心标准化,为了方便将标准化后的数据矩阵仍然记为X
3)求相关系数矩阵R, rij的定义如下

4)求R的特征方程
![]()
5)确定主成分的个数

6)计算m个相应的单位特征向量:
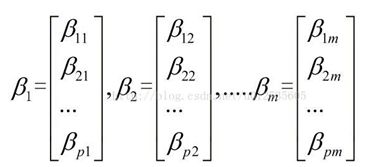
7)计算主成分

三、使用仪器、材料
WIN10系统、R-studio、Excel
四、实验步骤
1.下载数据,数据来源于kaggle。
2.数据预处理,筛选8个变量,对定类变量进行哑编码处理。
3.对8个变量进行主成分分析,提取4个主成分。
4.写出主成分表达式并解释各主成分的统计及意义。
5.绘制主成分载荷散点图、碎石图对主成分进行解释。
6.对样本回代预测,即计算各样本在主成分上的得分。
五、实验过程、结果及分析
(一)数据说明
原始数据拥有12个变量,其中8个定量变量,4个定类变量,自杀年份记载从1987年至2016年,数据条总计27821行。原始数据字段属性如下表所示:
| 字段 | 含义 |
|---|---|
| country | 国籍 |
| year | 年份 |
| sex | 性别 |
| age | 年龄区间 |
| suicides_no | 自杀数量 |
| population | 人口数量 |
| suicides/100k pop | 每10w人的自杀率 |
| country-year | 国家年份 |
| HDI for year | 人类发展指数 |
| gdp_for_year ($) | GDP |
| gdp_per_capita ($) | 人均国民生产总值 |
| generation | 属于哪一代人 |
由于选取的是影响自杀因素的自变量,故将数据集中的suicides_no(自杀数量)因变量舍去。HDI for year人类发展指数缺失项过多,且无法对缺失值进行补充,故舍去该列。存在年份和国家年份两个时间度量单位,选取年份国际通用度量单位。国家是定类数据,且存在101个类型并且各国的政治文化环境差异过大影响自杀率因素过于复杂,此文不把该变量考虑在内。
因此选取如下8个变量进行后续主成分分析。
| 字段 | 含义 |
|---|---|
| x1 | 年份 |
| x2 | 人口数量 |
| x3 | 每10w人的自杀率 |
| x4 | GDP |
| x5 | 人均国民生产总值 |
| x6 | 属于哪一代人 |
| x7 | 年龄区间 |
| x8 | 性别 |
(二)数据预处理
1.缺失值处理
经检测无缺失值,无异常值。
2.数据标准化处理
八个指标的取值范围有较大的差异,采用标准差标准化来消除数量级数据的影响。
3.定类变量哑编码
对性别、年龄、时代3个类型变量进行编码处理。
| 性别 | 编号 |
|---|---|
| 男 | 0 |
| 女 | 1 |
| 年龄 | 编号 |
|---|---|
| 5-14years | 0 |
| 15-24years | 1 |
| 25-34 years | 2 |
| 35-54 years | 3 |
| 55-74 years | 4 |
| 75+ years | 5 |
| 时代 | 编号 |
|---|---|
| 二战大兵一代1900-1924 | 0 |
| 沉默的一代1925-1945 | 1 |
| 战后婴儿潮1946-1964 | 2 |
| X世代1965-1980 | 3 |
| 千禧一代1981-1994 | 4 |
| Z世代1995-2016 | 5 |
(三)主成分分析
1.计算样本相关系数矩阵
读取完数据后,求样本的相关性系数矩阵如下表所示:

用简洁的符号表示出相关系数矩阵
结合一图一表可以知道x1 年份与x5人均国民生产总值、x6出生时代之间有正相关性,x2人口和x4GDP有较强正相关性,x3每10万人自杀率与x6出生时代、x8性别存在负相关,与x7年龄存在正相关性。x4GDP与x5人均国民生产总值存在正相关性,x7年龄和X6出生时代有很强的负相关性。
初步认定,x1年份越大现代化程度越高发展逐步变好使得x5人均国民生产总值也随着时间推移而正向增长,而出生时代本身的定义就是对近一个世纪进行人为划分,编码的变量也是随着时间推移变大(0-5),与年份正相关是合理的。x7年龄和X6出生时代两个都是人为分类变量,出生时代越早与年龄越大是合理的。
X2人口越多,劳动力所占的比例也可能越多,即创造的社会财富越大推进x4GDP的正向发展。x4GDP越大 x5人均国民生产总值正向增长。
X6出生时代越早意味着处于二战大兵一代、和沉默的一代的可能性越大,而这两个年代一个战乱时期社会格局动荡另一个经济大萧条生活不稳定,与X3每10万人自杀率越高存在一定的相关性。并且x3与x8性别也存在负相关,由于X8是二分类变量,0是男性1是女性,性别变量越小意味着是男性时,x3的自杀率会越高。
2.确定主成分个数及表达式
对这8个因子做主成分分析求取样本相关矩阵的特征值和主成分载荷,运行结果如下:

由程序运行结果可知主成分的标准差,即相关系数矩阵的8个特征值开方各为:

从输出结果可以看出,前四个主成分的累积贡献率为0.2799+0.2270+0.1623+0.1496=0.8189,超过了80%,因此从8个主成分中提取4个主成分。
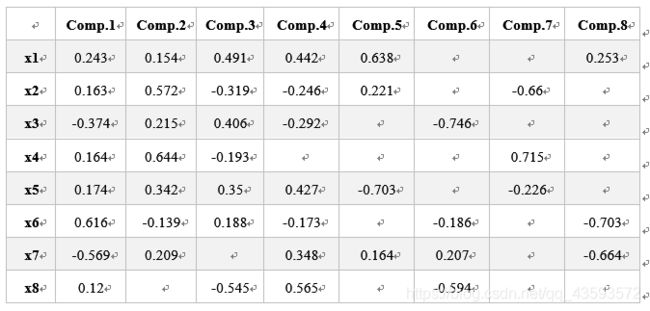
前4个主成分的式子如下图所示:

第一主成分在 x6和x7这两个指标上载荷值的绝对值比较大,且x6出生时代为正值,x7年龄为负值,出生时代离现在越近说明社会格局相比从前要更稳定些,可视为反映社会环境的主成分。
第二主成分在 x4 GDP和x2人口这两个指标上取值为正且载荷值较大,可视为反映经济发展水平的主成分。
第三主成分在 x8性别、x1年份和x3 每10w人自杀率这三个指标上载荷值的绝对值较大,可视为自杀传染倾向的主成分。
第四主成分在x8性别、x1年份、x5人均国民生产总值这3个指标上取正且载荷值较大可视为反映个体经济地位的主成分。
3.主成分解释
(1)主成分碎石图
以直方图的类型绘制主成分碎石图,如下图所示:

直观地看出来前4个主成分特征值都大于1,且前4个主成分的方差占了总方差变化地大部分,因此选取主成分的个数为4是恰当的。
(2)载荷散点图
使用主成分载荷矩阵的前4列数据绘制主成分的载荷散点图,下图1是第一主成分和第二主成分的载荷散点图,下图2是第三主成分和第四主成分的载荷散点图。

从图中可以很明显地看到第一主成分除了每10w人自杀率和年龄外,其他6个变量都在右侧正值,进一步反映社会环境水平。第二主成分GDP、人口、人均国民生产总值在正值的最上方,直观体现经济发展水平。

从图可以看到第三主成分的在年份和每10w人自杀率这2个指标上载荷值的绝对值较大,且为正值,可体现自杀传染倾向。第四主成分在性别、年份、人均国民生产总值这3个指标0轴上方反映个体经济地位。
4.样本回代预测
计算各样本在主成分上的得分,选取样本数据集的一前一尾作为实例。
 各样本在4个主成分上的得分绝对值较大的在上表结果中用粗体标出。
各样本在4个主成分上的得分绝对值较大的在上表结果中用粗体标出。
从第一主成分看,样本4、6号的主成分得分为负,且绝对值较大,说明这两个样本社会环境比较动荡,样本27818、27819号的主成分得分为正,且绝对值较大,说明这两个样本的社会环境比较稳定和谐。
从第二主成分看,样本1、3、5号的主成分得分为负,且绝对值较大,说明这三个样本经济发展水平较差。
从第三主成分看,样本3、6号的主成分得分为负,且绝对值较大,说明这两个样本自杀传染倾向比较低,样本1号的主成分得分为正,且绝对值较大,说明这一个样本的自杀传染倾向比较高。
从第四主成分看,样本1、5号的主成分得分为负,且绝对值较大,说明这两个样本个体经济地位比较低,样本27817的主成分得分为正,且绝对值较大,说明这个样本的个体经济地位比较高。
六、参考资料
《多元统计分析——基于R》第二版 费宇主编
千语_肉丸子___数据降维--------主成分分析(PCA)算法原理和实现学习笔记:https://blog.csdn.net/u012535605/article/details/70163357
七、附录
install.packages("lattice")
install.packages("MASS")
install.packages("nnet")
install.packages("mice")
install.packages("nnet")
library(lattice)
library(MASS)
library(nnet)
library(mice)
library(nnet)
##导入函数
##预处理
data1=read.csv("E:/桌面/大学/大三/大三下/多元统计分析/第三次作业/1985年至2016年自杀率概览/suicide4.csv",header=T)
sum(is.na(data1)) #计算缺失值数量
sum(complete.cases(data1)) #计算data中完整样本的数量
data=na.omit(data1)
#取前8列变量
a<-as.matrix(data1[,1:8])
colnames(a)<-NULL
d<-as.vector(scale(a)) #标准化处理#
#主成分分析
R=round(cor(d),3) #求样本相关系数矩阵,保留三位小数
R
symnum(cor(d,use="complete.obs")) ##用简洁的符号表示出相关系数矩阵中绝对值位于不同区间内的相关系数的位置
PCA=princomp(d,cor=T)
summary(PCA,loadings=T) #列出主成分分析结果
pre=round(predict(PCA),3)##预测,计算各样本的主成分得分
head(pre)
tail(pre)
screeplot(PCA,type="barplot")###碎石图,直方图形式
load=loadings(PCA)##提取主成分载荷矩阵
plot(load[,3:4],xlim=c(-1.0,1.0),ylim = c(-1.0,1.0)) #作第3、4个主成分的载荷散点图
abline(h=0,v=0)
rnames=c("年份","人口数量","每10w人的自杀率","GDP","人均国内生产总值","时代","年龄","性别")
text(load[,3],load[,4],labels = rnames)
biplot(PCA,scale=0.5) ##绘制样本点关于X个主成分的图