学习笔记(4)——序列标注与隐马尔可夫模型
- 序列标注问题
-
- 序列标注与中文分词
- 序列标注与词性标注
- 序列标注与命名实体识别
- 隐马尔可夫模型
-
- 从马尔可夫假设到隐马尔可夫模型
- 初始状态概率向量
- 状态转移矩阵
- 发射概率矩阵
对于一个句子中相对陌生的新词,之前的分词算法识别不出,但人类可以根据构词法进行动态组词。所以我们需要更细粒度的模型,比词语更细粒度的就是字符。
只要将每个汉字组词时所处的位置(首尾等)作为标签,则中文分词就转化为给定汉字序列找出标签序列的问题。一般而言,由字构词是 序列标注模型 的一种应用。在所有“序列标注”模型中, 隐马尔可夫模型 是最基础的一种。
序列标注问题
序列标注指的是给定一个序列 x = x 1 x 2 … x n x=x_{1} x_{2} \ldots x_{n} x=x1x2…xn ,找出序列中每个元素对应标签 y = y 1 y 2 … y n y=y_{1} y_{2} \ldots y_{n} y=y1y2…yn 的问题。其中,y 所有可能的取值集合称为标注集 。比如,输入一个自然数序列,输出它们的奇偶性。
求解序列标注问题的模型一般称为序列标注器 ,通常由模型从一个标注数据集 { X , Y } = { ( x ( i ) , y ( i ) ) } , i = 1 , … , K \{X, Y\}=\left\{\left(x^{(i)}, y^{(i)}\right)\right\}, i=1, \ldots, K {X,Y}={(x(i),y(i))},i=1,…,K 中学习相关知识后再进行预测。NLP问题中,x 通常是字符或词语,而 y 则是待预测的组词角色或词性等标签。中文分词、词性标注以及命名实体识别,都可以转化为序列标注问题。
序列标注与中文分词

分词标注集 并非只有一种,为了捕捉汉字分别作为词语首尾 (Begin、End) 、词中(Middle) 以及单字成词(Single) 时不同的成词概率,人们提出了 {B,M,E,S} 这种最流行的标注集。
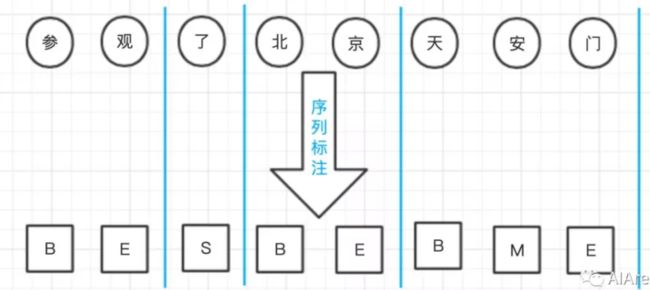
序列标注与词性标注
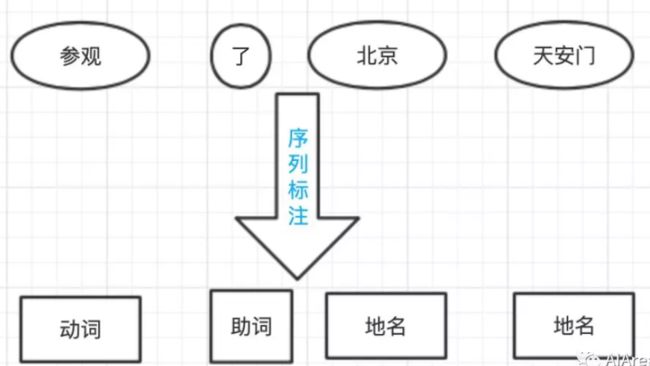
词性标注任务是一个天然的序列标注问题:x 是单词序列,y 是相应的词性序列。需要综合考虑前后的单词与词性才能决定当前单词的词性。
序列标注与命名实体识别
所谓命名实体 ,指的是现实存在的实体,比如人名、地名和机构名,命名实体是 OOV(Out of Vocabulary,即未登录词) 的主要组成部分。
考虑到字符级别中文分词和词语级别命名实体识别有着类似的特点,都是组合短单位形成长单位的问题。所以命名实体识别可以复用BMES标注集 ,并沿用中文分词的逻辑,只不过标注的对象由字符变为单词而已。唯一不同的是,命名实体识别还需要确定实体所属的类别,可以通过将命名实体类别附着到BMES标签来达到目的。比如,构成地名的单词标注为“B/M/E/S-地名”,以此类推。对于那些不构成命名实体的单词,则统-标注为O ( Outside), 即复合词之外。

隐马尔可夫模型
隐马尔可夫模型( Hidden Markov Model, HMM) 是描述两个时序序列联合分布 p(x,y) 的概率模型: x 序列外界可见(外界指的是观测者),称为观测序列(obsevation sequence); y 序列外界不可见,称为状态序列(state sequence)。隐马尔可夫模型之所以称为“隐”,是因为从外界来看,状态序列(例如词性)隐藏不可见,是待求的因变量。从这个角度来讲,人们也称状态为隐状态(hidden state),而称观测为显状态( visible state)。隐马尔可夫模型之所以称为“马尔可夫模型”,”是因为它满足马尔可夫假设。
从马尔可夫假设到隐马尔可夫模型
马尔可夫假设 :每个事件的发生概率只取决于前一个事件。
马尔可夫链 :将满足马尔可夫假设的连续多个事件串联起来,就构成了马尔可夫链。
如果把事件具象为单词,那么马尔可夫模型就具象为二元语法模型。
隐马尔可夫模型 :它的马尔可夫假设作用于状态序列,
- 假设 ① :当前状态 Yt 仅仅依赖于前一个状态 Yt-1, 连续多个状态构成隐马尔可夫链 y。
- 假设 ②: 任意时刻的观测 x 只依赖于该时刻的状态 Yt,与其他时刻的状态或观测独立无关。
如果用箭头表示事件的依赖关系(箭头终点是结果,依赖于起点的因缘),则隐马尔可夫模型可以表示为下图所示:

状态与观测之间的依赖关系确定之后,隐马尔可夫模型利用三个要素来模拟时序序列的发生过程——即初始状态概率向量 、状态转移概率矩阵 和发射概率矩阵。
初始状态概率向量
系统启动时进入的第一个状态 Y1 称为初始状态,假设 y 有 N 种可能的取值,那么 Y1 就是一个独立的离散型随机变量,由 P(y1 | π) 描述。其中:
π = ( π 1 , ⋯ , π N ) T , 0 ⩽ π i ⩽ 1 , ∑ i = 1 N π i = 1 \pi=\left(\pi_{1}, \cdots, \pi_{N}\right)^{\mathrm{T}}, 0 \leqslant \pi_{i} \leqslant 1, \sum_{i=1}^{N} \pi_{i}=1 π=(π1,⋯,πN)T,0⩽πi⩽1,∑i=1Nπi=1
是概率分布的参数向量,称为初始状态概率向量。
给定 π ,初始状态 Y1 的取值分布就确定了,比如采用{B,M,E,S}标注集时概率如下:
p ( y 1 = B ) = 0.7 p\left(y_{1}=B\right)=0.7 p(y1=B)=0.7
p ( y 1 = M ) = 0 p\left(y_{1}=M\right)=0 p(y1=M)=0
p ( y 1 = E ) = 0 p\left(y_{1}=E\right)=0 p(y1=E)=0
p ( y 1 = S ) = 0.3 p\left(y_{1}=S\right)=0.3 p(y1=S)=0.3
此时隐马尔可夫模型的初始状态概率向量为 π=[0.7,0,0,0.3],注意,句子第一个词是单字的可能性要小一些。
状态转移矩阵
根据马尔可夫假设,t+1 时的状态仅仅取决于 t 时的状态,既然一共有 N 种状态,那么从状态 Si 到状态 Sj 的概率就构成了一个 N×N 的方阵,称为状态转移矩阵 A:
A = [ p ( y t + 1 = s j ∣ y t = s i ) ] N × N A=\left[p\left(y_{t+1}=s_{j} \mid y_{t}=s_{i}\right)\right]_{N \times N} A=[p(yt+1=sj∣yt=si)]N×N
其中下标 i、j 分别表示状态的第 i、j 种取值。状态转移概率的存在有其实际意义,在中文分词中,标签 B 的后面不可能是 S,于是就有 P(Yt+1 = S | Yt = B) = 0。同样,词性标注中的“形容词->名词”“副词->动词”也可通过状态转移概率来模拟,这些概率分布参数不需要手动设置,而是通过语料库上的统计自动学习。
发射概率矩阵
根据隐马尔可夫假设②,当前观测 Xt 仅仅取决于当前状态 Yt。也就是说,给定每种 y,x 都是一个独立的离散型随机变量,其参数对应一个向量。假设观测 x 一共有 M 种可能的取值,则 x 的概率分布参数向量维度为 M。由于 y 共有 N 种,所以这些参数向量构成了 N×M 的矩阵,称为发射概率矩阵B。
/ B = [ p ( x t = o i ∣ y t = s j ) ] N × M / \boldsymbol{B}=\left[p\left(x_{t}=o_{i} \mid y_{t}=s_{j}\right)\right]_{N \times M} /B=[p(xt=oi∣yt=sj)]N×M
其中,第 i 行 j 列的元素下标 i 和 j 分别代表观测和状态的第 i 种和第 j 种取值。
参考文献
《自然语言处理入门》详细笔记——4. 隐马尔可夫模型与序列标注