蓝桥每日一点题,国赛场上ta和你
目录
-
- 第一题 巧排扑克牌
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 第二题 质数拆分
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 第三题 日志统计
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 第四题 递增三元组
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 第五题 外卖点优先级
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
第一题 巧排扑克牌
题目描述
原题传送门
解题报告
这个题我不太知道怎么落实到代码上,不知道有没有小伙伴能够指点一下关于代码落实的事儿了,我这儿就直接草稿纸上进行演算,然后直接输出结果吧。
推导的图示如下:
a[0] ~ a[12]分别代表手上拿的这13扑克牌

此时就可以很清楚的看到原本a[0]到a[12]对应的扑克牌是多少了。
参考代码(C++版本)
#include
int main()
{
//我感觉比较坑的是,题目中好像没有说它们之间有空格嘛....
printf("7, A, Q, 2, 8, 3, J, 4, 9, 5, K, 6, 10");
return 0;
}
第二题 质数拆分
题目描述
原题传送门
解题报告
这个题,我唯一想说的了,就是读题时候仔细一点。
我原本以为是很呆萌的凑来两个质数相加等于2019了。都准备拿出才学的双指针进行练手了,然后就WA了。
题目中说的是若干两两不同的质数。意思就是用很多质数进行组合,但是每个质数是唯一的,只能用一次,现在让找到一个最优解,那么这个就是可爱的01背包呀。
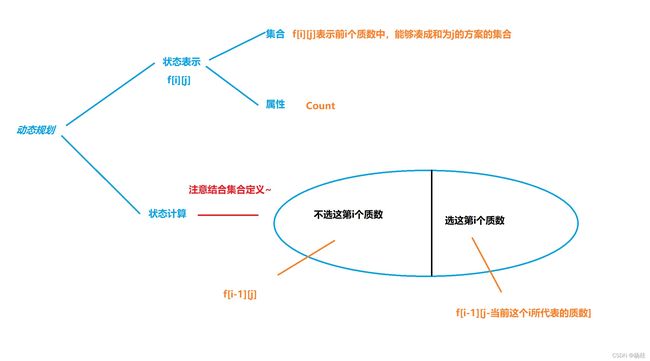
拿出咱们可爱的闫式DP分析法
状态表示:
集合: f [ i ] [ j ] f[i][j] f[i][j]表示前 i i i个质数中能够构成和为 j j j的方案个数
属性: C o u n t Count Count
因为这个集合f[i][j]最终还是依旧是一块存储空间,要存储一个数据的,我们就泛泛的将这个数据称为f[i][j]的一个属性
状态计算:
状态计算的本质是依旧最后一个不同点,对当前已经确定的集合f[i][j]进行划分。
对于01背包而言,这个题的划分依旧就是当前这个质数选还是不选。
这里写的是二维DP哈,它这个是可以优化为一维的,因为后面内容比较多,我就不讲优化了,以后出关于优化的博客~
参考代码(C++版本)
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 2030;
bool st[N];
int primes[N],cnt;
LL f[N][4200]; //f[i][j]表示在前i个质数中能够构成和为j的方案个数
//线性筛把质数搞出来
void get_primes(int n)
{
for(int i = 2;i <= n;i++)
{
//如果是质数,就把加到数组中去
if(!st[i]) primes[++cnt] = i;
//从小到大枚举所有的质数
for(int j = 0; primes[j] <= n/i;j++)
{
//把prims[j] * i筛掉
st[primes[j] * i] = true;
}
}
}
int main()
{
//用筛法先把2-2019的所有质数都筛出来
get_primes(2019);
//每个数只能用一次,那么就可以摸出可爱的01背包了
//初始化
f[0][0] = 1;
for(int i = 1; i <= cnt;i++)
for(int j = 0;j <= 2019;j++)
{
f[i][j] += f[i-1][j];
if(j >= primes[i]) f[i][j] += f[i-1][j-primes[i]];
}
cout << f[cnt][2019] << endl;
return 0;
}
第三题 日志统计
题目描述
原题传送门
解题报告
它给的标签是贪心,但是我刚好在学双指针,那就用双指针来写吧,刚好我也不太会贪心~,其实我也太不是很会双指针,可恶。
双指针算法:让一个指针 i i i在前面,走得慢,另一个指针 j j j,走的快,和 i i i指针形成一个区间。
对于这个题而言: 先把每个获赞的帖子,将它存起来。
再去校验帖子是否在规定的时间差 d d d下获得 K K K个赞。倘若是,那么这个帖子就是热帖,
参考代码(C++版本)
#include
#include
#include
#include
#define x first
#define y second
using namespace std;
typedef pair PII;//当输入的信息是一个二元组的时候,就要么使用pair,要么自己定义结构体
const int N = 100010;
int n,d,k;
PII logs[N];;//用于存储日志ts, id
int cnt[N];//用来标记帖子的id号
bool st[N];//用来记录一个id号获得的赞数,表示形式为cnt[id]++;
int main()
{
//处理读入
scanf("%d%d%d",&n,&d,&k);
for(int i = 0; i < n;i++) scanf("%d%d",&logs[i].x,&logs[i].y);
//按照时间顺序进行排序
sort(logs,logs+n);
// 枚举每个帖子
for(int i = 0,j = 0; i < n;i++)
{
int id = logs[i].y;//把每个获赞的帖子id存起来
cnt[id] ++;;//获得一个赞,所以此刻 ++
while(logs[i].x - logs[j].x >= d)
{
cnt[logs[j].y] --; //把这个不符合要求的贴扣除去
j ++;//要把指针j向后移动
}
if(cnt[id] >= k) st[id] = true;
}
// 把热帖的id打印出来
for(int i = 0;i <= 100000;i++)
if(st[i]) printf("%d\n",i);
return 0;
}
第四题 递增三元组
题目描述
原题传送门
解题报告
倘若直接三重循环枚举,那么就是 1 0 15 10^{15} 1015次的运算,远远大于了C++ 一秒能够进行的一亿次运算,那么是肯定要超时的。
结合我在壹之型放的根据数据范围确定算法中可以看到,假如数据范围是 1 0 5 10^5 105,那么我们最多是只能进行一层循环的。

因为B序列可以是在A序列和C序列的中间。刚好可以做到很好的联动,因此咱们待会决定枚举它吧。
按照题目要求,
我们需要找到 A A A序列中比 B i B_i Bi小的数,统计出它们的个数;
找到 C C C序列中比 B i B_i Bi大的,统计它们的个数。
最后根据出可爱的乘法原理(小学数学内容),就可以得到结果了
为了统计出A序列中小于 B i B_i Bi的个数,C序列中大于 B i B_i Bi的个数。
可以先排序,再结合着二分查找。
也可以用前缀和,先将A序列和C序列进行初始化,初始化环节统计的是个数,出现过就算作1,没有出现过就算作0。
统计A序列中小于 B i B_i Bi的个数,那么相当于在前缀和数组中查找 0 0 0 ~ B i − j B_i-j Bi−j有多少个数。
统计B序列中大于 B i B_i Bi的个数,那么相当于在前缀和数组中查找 B i B_i Bi ~ N − 1 N-1 N−1有多少个数。
参考代码(C++版本)
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int a[N],b[N],c[N];
int a_b[N];//a_bi] 表示在A[]中有多少个数小于b[i]的个数
int c_b[N];//c_b[i] 表示在C[]中有多少个数大于b[i]的个数
int cnt[N],s[N]; //用于统计的cnt数组以及用于计算前缀和的s数组
int main()
{
scanf("%d",&n);
//读入三个三元组
//因为要用到前缀和的知识,前缀和中会有减一的操作,为了不出现数组角标越界,所有需要对输入的结果都+1
for(int i = 0; i < n;i++) scanf("%d",&a[i]),a[i] ++;
for(int i = 0; i < n;i++) scanf("%d",&b[i]),b[i] ++;
for(int i = 0; i < n;i++) scanf("%d",&c[i]),c[i] ++;
//求as[]
//先统计这个a[i]出现的次数
for(int i = 0; i < n;i++) cnt[a[i]] ++;//用cnt数组统计,意思就是,出现了就是1,没有出现就是0
for(int i = 1; i < N;i++) s[i] = s[i-1] +cnt[i]; //进行前缀和的初始化
for(int i = 0; i < n;i++) a_b[i] = s[b[i]-1];//统计(0,到Bj-1)的前缀和,因为这个前缀和记录的是个数,就可以用O(1)实现查询
//求cs[]
//先将cnt和s数组都清空
memset(cnt,0,sizeof cnt);
memset(s,0,sizeof s);
for(int i = 0; i < n;i++ ) cnt[c[i]] ++;
for(int i = 1; i < N;i++) s[i] = s[i-1] + cnt[i];
for(int i = 0; i < n;i++) c_b[i] = s[N-1] - s[b[i]];//这里就统计s[N-1]到b[i]的就好
//根据数据范围定算法这里我们确定了我们只能枚举一个数
//枚举每一个b[i]
LL res = 0;
for(int i = 0; i < n;i++) res += (LL)a_b[i] * c_b[i];
cout << res << endl;
return 0;
}
第五题 外卖点优先级
题目描述
解题报告
处理离散数据的思想——因为对于一个店铺而言,可能一段时间有订单,一段时间又没有订单了。
因此数据是离散的。处理的方式可以把连续没有订单的时刻先忽略了,放到有订单之后来处理。
解题思想:
| 这个模拟题稍微有点复杂,假如小伙伴有写伪代码的习惯,那么在解决较为复杂的模拟题时,可以更舒服一些 |
1、将所有订单按照时间排序
2、然后从前向后枚举每个订单
纯暴力是枚举的每一个时刻,时间复杂度是 O ( N 2 ) O(N^2) O(N2),会超时的。
在循环中,每次处理的是一批相同的订单了(可以理解为,只要这个时间点和其对应的店铺Id是相同的,就把它们看做一个整体,实现每次处理一批订单)
![]()
假设当前订单为第 i i i个,利用循环判断后面有没有相同的订单(也就是在相同的订单时间 t t t,店铺的编号 i d id id相同)。
当到第 j j j个订单时,订单不相同了,那么此时这批订单的数量应该是 c n t = j − i cnt= j - i cnt=j−i
下次 f o r for for循环从j从开始处理下一批订单
| 记录此时t和id,计算id的优先权,有两部分需要处理 |
第一部分:
计算上一个拿到订单的时间 l a s t [ i d ] last[id] last[id]和 t t t之间,因为没有订单,所有都要减1,那么没有订单的数量是 t − l a s t [ i d ] − 1 t-last[id]-1 t−last[id]−1(最后要补一个-1是因为, t t t和 l a s t [ i d ] last[id] last[id]都有订单,比如2和5,第2时刻和第3时刻都有订单,那么没有订单的时刻就是3,4)
计算优先权,如果此时为负值,那么将优先权重置为0。
如果优先权小于等于3了,将这个店铺从优先缓存中剔除,即 : s t [ i d ] = f a l s e st[id] = false st[id]=false
第二部分:
t t t时刻拿到订单,并且数量为 c n t cnt cnt,这个店铺的优先权要加上 2 ∗ c n t 2*cnt 2∗cnt。
计算优先权,如果大于5,放入优先缓存中 ,即: s t [ i d ] = t r u e st[id] = true st[id]=true;
| 因为相同的订单已经处理过了,就不需要再计算了,直接到j这个出现下一批订单的位置开始新的一轮循环。 |
for(int i = 0; i < m;)
......
i = j;
循环到最后,将上一次拿到订单的时间 l a s t [ i d ] last[id] last[id]更新为 t t t
3、最后的处理
如果最后一个订单的时刻为T,那么倒是不用处理了。
如果不是T,那么最后一个订单到T时刻这部分扣除优先级的减法需要我们补上。
即,减去最后一个订单时刻与T的差值。因为T时刻也没有订单,所有这里不用减一了。
判断优先级,假如小于等于3,清除出优先缓存中。最后遍历优先缓存,得到的数量就是题目的答案
参考代码(C++版本)
#include
#include
#include
#include
#define x first
#define y second
using namespace std;
typedef pair PII;
const int N = 100010;
int n,m,T;
int score[N];//表示第i个店铺的优先级
int last[N];//表示第i个店铺上次没有订单的时刻
bool st[N];//表示第i个店铺当前是否处于优先缓存中
PII order[N];
int main()
{
scanf("%d%d%d",&n,&m,&T);
//因为订单信息是一个二元组,所有这里使用pair来读入一个二元组
for(int i = 0; i < m;i++) scanf("%d %d",&order[i].x,&order[i].y);
//进行一步排序:pair是自带比较函数的,按照第一关键字first进行,倘若第一关键字相同,考虑第二关键字
sort(order,order+m);
//枚举每个订单
for(int i = 0; i < m;)
{
int j = i;
//找到m个订单中,相同的订单
while(j < m && order[j] == order[i]) j++;
int t = order[i].x;//获取订单时间
int id = order[i].y;//获取订单id
int cnt = j-i; //获取数量
i = j;//将j赋值给i,处理下一批订单
score[id] -= t - last[id] - 1;//扣除掉t时刻内,没有订单时候的优先级
if(score[id] < 0) score[id] = 0;//如果优先级扣成负数了,重置为0
if(score[id] <= 3) st[id] = false;//将这个店铺从优先缓存中抽出来
//以上是t时刻之前的信息
score[id] += cnt * 2;
if(score[id] > 5) st[id] = true;
//更新last[id]
last[id] = t;
}
//枚举每一个店铺
for(int i = 1; i <= n;i++)
if(last[i] < T) //如果到最后的这段时间中,确实没有订单了,就扣除相应的
{
score[i] -= T - last[i];
if(score[i] <= 3) st[i] = false;
}
int res = 0;
//最后统计有多少个店铺在优先缓存中
for(int i = 1;i <= n;i++) res += st[i];
//输出结果
printf("%d\n",res);
return 0;
}