VQLS：变分量子算法解线性方程组

复现的算法为VQLS算法，用于处理线性方程组$Ax=b$的问题。
这是一种变分量子算法，即用一个经典的优化器来训练一个含参的量子电路，整个算法的思路有些类似机器学习。
代码参考了qiskit提供的VQLS示例

10.17日晚重新看了一遍论文，才发现自己弄错了很多概念，例如：误以为分解$A$是为了作为量子态输入到电路，实际上他是作为门矩阵作用于含参$x$的

流程分析

我大致将该算法分为一下4个流程。

1. 搭建含参电路
2. 计算损失函数
3. 优化器进行梯度下降
4. 求解得标准化后的x

图1 算法整体框架

1. 搭建含参电路

输入量子电路的为试探态，一般选择全$|0⟩$态，通过含参电路后，则可得：
$$|x(\alpha )⟩=V(\alpha )|0⟩$$
其中$V(\alpha )$为含参电路的等效矩阵。

将$A$分解为U矩阵和的形式来作为门电路：$$A=\sum c_n{A}_n$$上式中 $c_n$ 均为复数，这意味着可以将我们可以将$A_n$分别作为量子电路的门电路。

然后让带参数的$x(\alpha )$分别通过$A_n$再累加，得到$Ax(\alpha )$，接着就是构建一个损失函数，用于评估$Ax(\alpha )$与$b$的接近程度，可以理解为判别两个向量是否在同一方向上。

这一部分对用于图1中的蓝框部分。

2.损失函数

论文中提出两种损失函数，分别对应local和global。
global损失函数如下：
$$\begin{array}{rl}\widehat{C_G}=& tr(|\psi ⟩⟨\psi |(I-|b⟩⟨b|))\\ =& ⟨x|H_G|x⟩\end{array}$$
其中$H_G=A^{+}(I-|b⟩⟨b|)A，|x⟩=V(\alpha )|0⟩$
进行归一化则有：
$$\begin{array}{r}{C}_G=1-|⟨b|\Psi ⟩{|}^2\end{array}$$
其中$|\Psi ⟩=\frac{|\psi ⟩}{\sqrt{⟨\psi |\psi ⟩}}$。

local损失函数：$$\begin{array}{r}\widehat{C_L}=⟨x|H_L|x⟩\end{array}$$
其中$H_L=A^{+}U(I-\frac{1}{n}{\sum }_{j=1}^n(|0_j⟩⟨0_j|\otimes I_j))U^{+}A$。
对其进行归一化则有：$$\begin{array}{r}{C}_L=\frac{\widehat{C_L}}{⟨\psi |\psi ⟩}\end{array}$$

论文中提出局部损失函数相较于全局损失函数具有更好的梯度下降效果，如图2所示，局部损失函数能够在更少的迭代次数中达到梯度消失。

图2 两种损失函数对比

为了提高运算效率，这一步在量子计算机中进行，对应于图1中的红框部分。

复现过程中，我选择的是global损失函数。

3.优化器

在优化其中，主要实现的功能为：

• 计算损失函数
• 进行进行梯度下降

由步骤2分析可知，损失函数需要计算的有两个式子：
$$\begin{array}{rl}{\hat{C}}_G& =1-\frac{|⟨b|\psi ⟩|}{⟨\psi |\psi ⟩}\\ ⟨\psi |\psi ⟩& =⟨0|V(\alpha {)}^{+}{A}^{+}AV(\alpha )|0⟩\\ & =\sum _m\sum _n{c}_m^{\ast }{c}_n⟨0|V(\alpha {)}^{+}{A}_m^{+}{A}_{n}V(\alpha )|0⟩\\ |⟨b|\psi ⟩{|}^2& =\sum _m\sum _n{c}_m^{\ast }{c}_n⟨0|U^{+}{A}_{n}V(\alpha )|0⟩⟨0|V(\alpha {)}^{+}{A}_{m}U|0⟩\\ & =\sum _m\sum _n{c}_m{c}_n⟨0|U^{+}{A}_{n}V(\alpha )|0⟩⟨0|U^{+}{A}_{m}V(\alpha )|0⟩\end{array}$$
其中$U|0⟩=|b⟩$

Hadamard Test

该电路主要作用是对任给的幺正算符$U$和量子态$|\Psi ⟩$，可以给出该幺正算符在量子态上的投影期望 $⟨\Psi |U|\Psi ⟩$，如图3所示。

图3 Hadamard Test电路

由推导可知：
$$\begin{array}{r}P(0)=\frac{1}{2}(1+Re⟨\psi |U|\psi ⟩)\\ P(1)=\frac{1}{2}(1-Re⟨\psi |U|\psi ⟩)\end{array}$$
则有：
$$\begin{array}{r}Re⟨\psi |U|\psi ⟩=P(0)-P(1)\end{array}$$

我们需要做的是，将$x(\alpha )$作为图3中的$|\psi ⟩$输入到电路，选取$A_n$作为$U$，通过测量第一个qubit的0、1的概率再分别乘以系数累加则可得$⟨\psi |\psi ⟩$

Hadamard Overlap Test

Hadamard Overlap Test电路是用于计算：
$$⟨0|U^{+}{A}_{n}V(\alpha )|0⟩⟨0|V(\alpha {)}^{+}{A}_{m}U|0⟩$$

图4 Hadamard Overlap Test电路

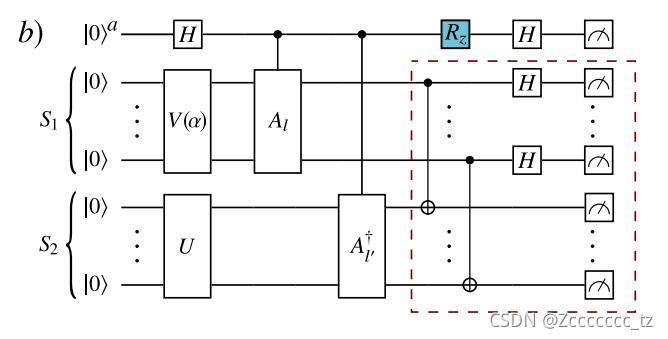
推导图4所示量子电路，可得：
$$P(0)-P(1)=Re(⟨0|U^{+}{A}_{l}V(\alpha )|0⟩⟨0|V(\alpha {)}^{+}{A}_l^{+}U|0⟩)$$
同样，通过测量第一个qubit的0、1的概率再分别乘以系数累加则可得$|⟨b|\psi ⟩{|}^2$

梯度下降

对于global损失函数，我们对其求梯度：
$$\begin{array}{r}\frac{\partial \widehat{C_G}}{\partial {\alpha }_i}=\sum _{m,n}{m}^{\ast }n\left(\frac{\partial ⟨0|V(\alpha {)}^{+}{A}_m^{+}{A}_{n}V(\alpha )|0⟩}{\partial {\alpha }_i}-\frac{\partial ⟨0|U^{+}{A}_{n}V(\alpha )|0⟩⟨0|V(\alpha {)}^{+}{A}_{m}U|0⟩|0⟩}{\partial {\alpha }_i}\right)\end{array}$$

最后经过迭代，得到最终的参数。这一部分对应图1中的绿框部分。

4.求解得标准化后的x

经过步骤3我们得到可以得到最终的量子电路参数，所有qubit位输入$|0⟩$，我们得到的是标准化后的$$|x⟩=\frac{x}{||x|{|}_2}$$

实践部分

量子电路搭建

含参电路

首先需要搭建的是含参电路，以3qubits电路，参数初始化全初始化为1为例，如图5所示。

图5 含参电路

代码如下，加入ry门以及cz门，ry门的参数作为可变参数，cz门使量子之间产生纠缠。

def apply_fixed_ansatz(circ, qubits, parameters):
    # 必须写为张量的形式
    parameters = paddle.to_tensor(parameters)
    parameters = paddle.reshape(parameters, [3, -1])
    for iz in range (0, len(qubits)):
        circ.ry(parameters[0][iz], qubits[iz])
    
    circ.cz([qubits[0], qubits[1]])
    circ.cz([qubits[2], qubits[0]])

    for iz in range (0, len(qubits)):
        circ.ry(parameters[1][iz], qubits[iz])

    circ.cz([qubits[1], qubits[2]])
    circ.cz([qubits[2], qubits[0]])

    for iz in range (0, len(qubits)):
        circ.ry(parameters[2][iz], qubits[iz])

Hadamard Test电路

再含参电路的基础上，搭建不同的U矩阵，计算$$⟨x(\alpha )|A_m^{+}{A}_n|x(\alpha )⟩$$
复现过程中取$$A=0.45Z_3+0.55I$$
故一共需要构建四种电路，分别对应$Z_3、I$的四种组合。
生成电路如图6所示（以$A_m=I,A_n=Z_3$为例）：

图6 Hadamard Test

代码如下所示：

def had_test(circ, gate_type, qubits, auxiliary_index, parameters):

    circ.h(auxiliary_index)

    apply_fixed_ansatz(circ, qubits, parameters)

    for ie in range (0, len(gate_type[0])):
        if (gate_type[0][ie] == 1):
            circ.cz([auxiliary_index, qubits[ie]])

    for ie in range (0, len(gate_type[1])):
        if (gate_type[1][ie] == 1):
            circ.cz([auxiliary_index, qubits[ie]])
    
    circ.h(auxiliary_index)

Hadamard Overlap Test电路

Hadamard Overlap Test电路是对Hadamard Test的推广，用于计算$$|⟨b|\psi ⟩{|}^2=\sum _m\sum _n{c}_m{c}_n⟨0|U^{+}{A}_{n}V(\alpha )|0⟩⟨0|U^{+}{A}_{m}V(\alpha )|0⟩$$

qiskit提供的VQLS示例中，取$A为8\ast 8$矩阵，$$b=[\sqrt{0.125},\sqrt{0.125},\sqrt{0.125},\sqrt{0.125},\sqrt{0.125},\sqrt{0.125},\sqrt{0.125},\sqrt{0.125}{]}^T$$
故取的$U=H_1{H}_2{H}_3$，如图7所示，

图7 U电路

最终生成的Hadamard Overlap Test电路如图8（由于jupyter生成的图片显示不全，选择在pycharm生成，建议paddle优化一下可视化效果）：

图8 Hadamard Overlap Test电路

同样也是对第一个qubit进行测量，然后乘系数累加则可得到$|⟨b|\psi ⟩{|}^2$
代码如下所示：

def special_had_test(circ, gate_type, qubits, auxiliary_index, parameters):

    circ.h(auxiliary_index)

    control_fixed_ansatz(circ, qubits, parameters, auxiliary_index)

    for ty in range (0, len(gate_type)):
        if (gate_type[ty] == 1):
            circ.cz([auxiliary_index, qubits[ty]])


    control_b(circ, auxiliary_index, qubits)
    
    circ.h(auxiliary_index)

优化器构建

这一部分同时参考paddle中VQE示例以及qiskit中示例，由于对双方的api都不熟悉，这一部分代码编写花费了很长时间，还存在着参数不能优化的bug以及我也无法验证loss计算过程是否存在问题。

loss计算

最开始使用paddle的优化器，由于api不熟悉，于是更换了scipy.optimize的minimize作为优化器
代码如下：

# 定义损失函数和前向传播机制
def calculate_cost_function(parameters):
    overall_sum_1 = 0# 参数1

    for i in range(0, len(gate_set)):
        for j in range(0, len(gate_set)):
            # 用hadmard-test电路计算loss的一个值
            cir_loss1 = UAnsatz(4)


            multiply = coefficient_set[i]*coefficient_set[j]
            had_test(cir_loss1, [gate_set[i], gate_set[j]], [1, 2, 3], 0, parameters)
            cir_loss1.run_state_vector()
            result = cir_loss1.measure(shots = 0, which_qubits = [0])
            # print(result['1'])
            overall_sum_1+=multiply*(1-(2*(result['1'])))
    print(overall_sum_1)

    overall_sum_2 = 0

    for i in range(0, len(gate_set)):
        for j in range(0, len(gate_set)):

            multiply = coefficient_set[i]*coefficient_set[j]
            mult = 1

            for extra in range(0, 2):

                cir_loss2 =  UAnsatz(5)

                if (extra == 0):
                    special_had_test(cir_loss2, gate_set[i], [1, 2, 3], 0, parameters)
                if (extra == 1):
                    special_had_test(cir_loss2, gate_set[j], [1, 2, 3], 0, parameters)

                cir_loss2.run_state_vector()
                result = cir_loss2.measure(shots = 0, which_qubits = [0])
                # print(result['1'])
                mult = mult*(1-(2*(result['1'])))

            overall_sum_2+=multiply*mult
    # print(overall_sum_2)
    loss = 1-float(overall_sum_2/overall_sum_1)
    # print(loss)
    return loss

如同前面分析

1. 先对$⟨\psi |\psi ⟩、|⟨b|\psi ⟩{|}^2$分开求解：搭建两个电路，输入全0态
2. 测量得到两个电路第一个qubit为1得概率$P(1)$，分别得到
   $$\begin{array}{rl}⟨\psi |\psi ⟩& =\sum _m\sum _n{c}_m^{\ast }{c}_n(1-2P(1))\\ |⟨b|\psi ⟩{|}^2& =\sum _m\sum _n{c}_m{c}_n(1-2P(1))\end{array}$$
3. 带入$$loss=1-\frac{|⟨b|\psi ⟩{|}^2}{⟨\psi |\psi ⟩}$$

参数优化器配置

out = minimize(calculate_cost_function, x0=[float(random.randint(0,3000))/1000 for i in range(0, 9)], method="COBYLA", options={'maxiter':100})
print(out)

运行结果如下：

图9 优化器运行结果

得到标准化后的x

图10 VQLS和numpy求解x对比（标准化后）

除了相差$\pi$的全局相位，我复现求解的$x$与真实标准化的$x$存在着排列顺序上以及的区别(我将示例中求解出来的电路参数带入也有相同的问题)

小结

复现过程中，发现的问题如下：

1. 对机器学习部分基础知识掌握不到位，对paddle的api调用不熟练
2. 量子计算理论部分还相当薄弱，对于测量、纠缠以及量子门对应的作用（尤其是多比特量子门）等部分不熟悉。