矩阵快速幂算法及相关应用(含python源码)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 一、快速幂算法(概述)
- 二、整数快速幂(源码)
- 三、矩阵快速幂(源码)
- 四、矩阵快速幂的应用
-
- 1.矩阵构造举例:
- 2.例题:
一、快速幂算法(概述)
①快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高。
②快速幂算法的核心思想就是每一步都把指数分成两半,而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。
③快速幂可以用位运算来实现,python实现为:
b & 1 #取b二进制的最低位,判断和1是否相同,相同返回1,否则返回0,可用于判断奇偶
b >> 1 #把b的二进制右移一位,即去掉其二进制位的最低位
二、整数快速幂(源码)
'''
首先,幂数会被表示为二进制系数,
其位数即为结果的项的个数,最后某项是否被乘进去需要看此项的系数是否为1,若为0则
'''
x=int(input())
n=int(input())
def quick_power(x, n):
# 特殊情况
if n == 0:
return 1
# 递归过程的最后一层
elif n == 1:
return x
# 如果幂的值为偶数, 则 不 进行记录,传给下一层
else:
y=quick_power(x,n//2)#递下去
print(y)
if(n&1):#n的末位是不是1
return (y**2)*x
return(y**2)
print(quick_power(x, n))
三、矩阵快速幂(源码)
跟整数快速幂一样,但是平方需要重写一个矩阵乘法的函数,如果有取模的需要也应该在此函数中体现。此处举例模99999999,代码如下:
##矩阵快速幂算法(递归法
def matrix_mul(A, B):
#矩阵乘法函数,返回两个矩阵相乘的值,建议背诵
return [[sum(a * b % 99999999 for a, b in zip(col, row)) % 99999999 for col in zip(*B)] for row in A]
def matrix_pow(A, n):
size_ = len(A)
if n == 0:#返回单位矩阵
res = [[0 for _ in range(size_)] for _ in range(size_)]
for i in range(size_):
res[i][i] = 1
return res
elif n == 1:#返回自己
return A
else:
y = matrix_pow(A, n // 2)
if n & 1:#要乘
return matrix_mul(matrix_mul(y, y), A)
return matrix_mul(y, y)#不乘
四、矩阵快速幂的应用
可以通过构造快速幂矩阵来求递推式,比如斐波那契数列等等,
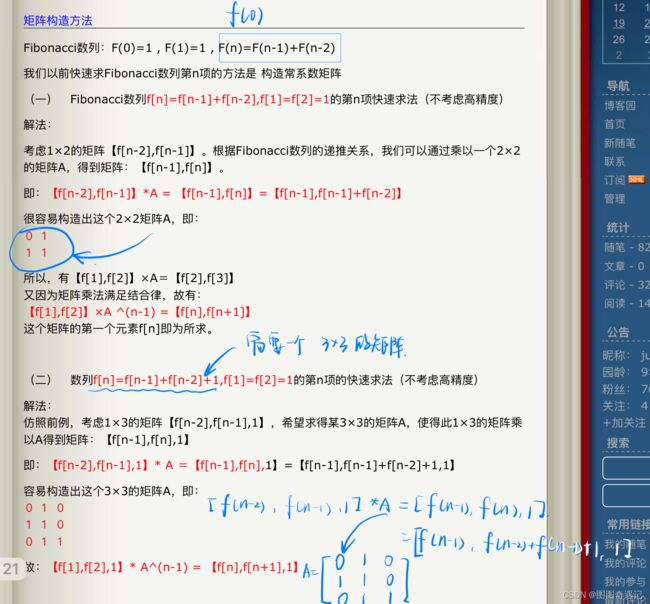
1.矩阵构造举例:
2.例题:
以下面这道题为例说明具体应用:

①给出了六个初始值,需要构造6*6的二维矩阵
②构造出的矩阵应能使前一个向量变成它递推的后一个向量(即n+1)
③通过对此矩阵的快速幂乘法,得到递推n次后的值,进而求出结果
其代码如下:
##矩阵快速幂算法(递归法
def matrix_mul(A, B):
#矩阵乘法函数,返回两个矩阵相乘的值,建议背诵
return [[sum(a * b % 99999999 for a, b in zip(col, row)) % 99999999 for col in zip(*B)] for row in A]
def matrix_pow(A, n):
size_ = len(A)
if n == 0:#返回单位矩阵
res = [[0 for _ in range(size_)] for _ in range(size_)]
for i in range(size_):
res[i][i] = 1
return res
elif n == 1:#返回自己
return A
else:
y = matrix_pow(A, n // 2)
if n & 1:#要乘
return matrix_mul(matrix_mul(y, y), A)
return matrix_mul(y, y)#不乘
matrix = [[0, 1, 0, 0, 2, 0, 5],
[1, 0, 0, 0, 3, 2, 3],
[1, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1]] #构造的矩阵
ini = [[6], [5], [1], [4], [2], [3], [1]] #初始值
a = matrix_mul(matrix_pow(matrix, int(input()) - 1), ini) #幂数减去第一个,乘上初始的
print(a[-3][0] % 99999999, a[-2][0] % 99999999, sep='\n') #输出第n个值