基于强化学习与深度强化学习的游戏AI训练

github地址

一、摘要

在本次大作业中由两个项目组成。

第一个小项目即为简单AI走迷宫游戏，通过强化学习的Q-learning算法，对AI进行训练来让其能以大概率找打一条通关路径并基本按照该路径进行移动。第二个小项目基于Gym库提供的Atari游戏Pong，通过深度强化学习的DQN算法，对AI进行训练来让其能与机器进行弹球对战。

二、引言

第一个项目通过利用强化学习中的Q-learning算法，实现了游戏AI去游玩走迷宫游戏并且找到最大概率通过迷宫的目标。这个项目主要利用了强化学习的入门知识去实现简单的走迷宫游戏例子，并通过训练我们自己的AI去从重重障碍中走出迷宫。

第二个项目通过利用DQN算法，实现了Pong弹球小游戏中的AI训练。我们训练我们自己的AI完成Pong游戏。经过DQN算法对AI的训练，可以看到我们的AI胜率有了很大改善，从最开始几乎全输到几乎全胜。

三、研究方法

（一）项目一：Q-Learning算法在AI走迷宫游戏中的探索

1、Q-learning算法介绍

1.1. 什么是Q-learning：

Q-learning是一种用于机器学习的强化学习技术。 Q-learning的目标是学习一种策略，告诉Agent在什么情况下要采取什么行动。 它不需要环境模型，可以处理随机转换和奖励的问题。

对于任何有限马尔可夫决策过程（FMDP），Q学习找到一种最优的策略，即从当前状态开始，它在任何和所有后续步骤中最大化总奖励的预期值。在给定无限探索时间和部分随机策略的情况下，Q学习可以为任何给定的 FMDP 确定最佳动作选择策略。“Q”命名函数返回用于提供强化的奖励，并且可以说代表在给定状态下采取的动作的“质量”。

1.2. 强化学习(Reinforcement learning)

强化学习涉及一个代理(Agent)，一组状态S(state)，以及一组动作A(action)。通过在状态中执行动作从而切换到另一个状态。在特定状态下执行动作为Agent提供奖励(reward) Agent的目标是最大化其总（未来）奖励。 它通过将未来状态可获得的最大奖励添加到实现其当前状态的奖励来实现这一点，从而通过潜在的未来奖励有效地影响当前行动。 该潜在奖励（价值）是从当前状态开始的所有未来步骤的奖励的预期值的加权总和。

例如：考虑登上火车的过程，其中奖励是通过登上火车总时间的负值来衡量的（值越小代表登上火车时间越短，这是更优的选择）。 一种策略是一旦打开就进入火车门，最大限度地缩短了自己的初始等待时间。 然而，如果火车很拥挤，那么在你进入大门的最初动作之后你将会进入缓慢状态，因为当你试图登上火车时，其他上火车的人会将你推离火车。 总的登上火车时间（成本）是：
0秒等待时间+ 15秒上车时间
第二天，通过随机机会（探索），你决定等待并让其他人先离开。 这最初导致更长的等待时间。 但是，由于其他上车人竞争，于是你可以更快的登上火车。 总体而言，此路径的奖励高于前一天，因为总的登上火车时间现在是：
5秒等待时间+ 0秒上车时间
通过探索，尽管最初行动导致更大的成本（或负面奖励），而不是强有力的策略，总体成本更低，从而揭示了更有价值的策略。

2、Q表(Q-table)

在训练过程中需要对游戏中遇到的场景的一些选择情况进行保存，因此可以建立如下的表

Q-table	Action1	Action2	Action3	Action4
State1	Q (s1, a1)	Q (s1, a2)	Q (s1, a3)	Q (s1, a4)
State2	Q (s2, a1)	Q (s2, a2)	Q (s2, a3)	Q (s2, a4)
State3	Q (s3, a1)	Q (s3, a2)	Q (s3, a3)	Q (s3, a4)

如上表所示，Q表中保存了在游戏进程中所将遇到的若干个场景，以及在场景中Agent将会遇到的所有情况下所能做出的相应应对动作选择（离散的），而每一个Q值所代表的就是在当前环境状态下，所选择了某个动作来应对之后在游戏结束时所Agent期望所能得到的分数。

由于我们所做的走迷宫demo的环境状态和对应的动作都是离散的，因此可以利用Q表来保存每轮训练的结果。

3、公式推导：

正如引言中所提到的，本子项目的主要目的是训练一个能够玩走迷宫游戏的AI并且在该游戏中拿到高分，因此我们的目标就是求出累计奖励最大的策略的期望：

Q-learning的主要优势就是使用了时间差分法TD（融合了蒙特卡洛和动态规划）能够进行离线学习, 使用bellman方程可以对马尔科夫过程求解最优策略。

通过bellman方程求解马尔科夫决策过程的最佳决策序列，状态值函数$V_{\pi }(s)$可以评价当前状态的好坏，每个状态的值不仅仅由当前状态决定，还需要由后面的状态决定，所以状态的累计奖励期望就可以得出当前$s$的状态值函数$V(s)$。

最优累计期望可用$V^{\ast }(s)$表示，可知最优解函数就是$V^{\ast }(s)=ma{x}_{\pi }{V}_{\pi }(s)$

$Q(s,a)$状态动作值函数

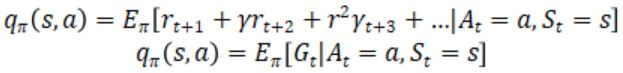
其中$G_t$是$t$时刻开始的总折扣奖励，从这里我们能看出来$\gamma$衰变值对$Q$函数的影响，$\gamma$越接近于1代表它越有远见会着重考虑后续状态的价值，当$\gamma$接近0的时候就会变得近视只考虑当前的利益的影响。所以从0到1，算法就会越来越会考虑后续回报的影响。

最优价值动作函数$Q^{\ast }(s,a)=ma{x}_{\pi }{Q}^{\ast }(s,a)$

Bellman方程实际上就是价值动作函数的转换关系

4、更新公式以及伪代码实现

根据以上推导可以对Q值进行计算，所以有了Q值我们就可以进行学习，也就是Q-table的更新过程，其中$\alpha$为学习率$\gamma$为奖励性衰变系数，采用时间差分法的方法进行更新。

上式就是Q-learning更新的公式，根据下一个状态$s^{\prime }$中选取最大的值$Q(s^{\prime },a^{\prime })$乘以衰变$\gamma$加上真实回报值做为Q现实，而根据过往Q表里面的$Q(s,a)$作为Q估计。

整个训练程序的伪代码如下：

1.Initialize Q arbitrarily //随机初始化Q值
2.Repeat (for each episode): //每一次游戏，从agent出发到游戏结束是一个episode
3.    Initialize S //agent处于初始位置(左上角)，S为初始位置的状态
4.    Repeat (for each step of episode):
5.        根据当前Q和位置S，使用一种策略，得到动作A //这个策略可以是ε-greedy等
6.        做了动作A，agent到达新的位置S'，并获得奖励R //奖励可以是1，50或者-1000
7.        Q(S,A) ← (1-α)*Q(S,A) + α*[R + γ* max Q(S', a)] //在Q中更新S
8.        S ← S'
9.until S is terminal //即到规定训练轮数为止

5、程序主要代码

① 从Q表中选取动作：

1.# 从Q-table中选取动作  
2.def get_action(self, state):  
3.    if np.random.rand() < self.epsilon:  
4.        # 贪婪策略随机探索动作  
5.        action = np.random.choice(self.actions)  
6.    else:  
7.        # 从q表中选择  
8.        state_action = self.q_table[state]  
9.        action = self.arg_max(state_action)  
10.    return action  

② 采样

1.# 采样   
2.    def learn(self, state, action, reward, next_state):  
3.        current_q = self.q_table[state][action]  
4.        # 贝尔曼方程更新  
5.        new_q = reward + self.discount_factor * max(self.q_table[next_state])  
6.        self.q_table[state][action] += self.learning_rate * (new_q - current_q) 

③ agent从Q表中选择出最优动作

1.#agent如何在Q表中选择出最优动作  
2.@staticmethod  
3.    def arg_max(state_action):  
4.        max_index_list = []  
5.        max_value = state_action[0]  
6.        for index, value in enumerate(state_action):  
7.            if value > max_value:  
8.                max_index_list.clear()  
9.                max_value = value  
10.                max_index_list.append(index)  
11.            elif value == max_value:  
12.                max_index_list.append(index)  
13.        return random.choice(max_index_list) 

（二）项目二：DQN算法在弹球游戏中的探索

1、DQN算法介绍

上一部分介绍关于Q-Learning的算法原理及DEMO实现流程，可以看出Q-Learning算法通过建立Q表完成了对于简单游戏的训练。在上面的简单分析中，我们使用表格来表示，但是这个在现实的很多问题上是几乎不可行的，因为状态实在是太多。使用表格的方式根本存不下，会造成维度爆炸问题。

以我们即将完成的Demo—Atari中的pong游戏为例：

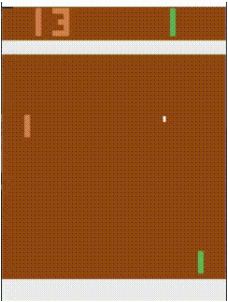
计算机玩Atari游戏的要求是输入原始图像数据，也就是210x160像素的图片，然后输出几个按键动作。总之就是和人类的要求一样，纯视觉输入，然后让计算机自己玩游戏。那么这种情况下，到底有多少种状态呢？有可能每一帧的状态都不一样。因此，从理论上看，如果每一个像素都有256种选择，那么就有：$256^{210\ast 160}$种状态。所以，我们是不可能通过表格来存储状态的。我们有必要对状态的维度进行压缩。

2、DQN算法原理解释

① 价值函数近似

说起来很简单，就是用一个函数来表示$Q(s,a)$，即$Q(s,a)=f(s,a)$。$f$可以是任意类型的函数$Q(s,a)=w_{1}s+w_{2}a+b$，其中$w_1,w_2,b$是函数$f$的参数。

通过函数表示，我们就可以无论$s$到底是多大的维度，最后都通过矩阵运算降维输出为单值的$Q$。因为我们并不知道$Q$值的实际分布情况，本质上就是用一个函数来近似$Q$值的分布，用$w$来统一表示函数$f$的参数，我们就可以得到$Q(s,a)\approx f(s,a,w)$。

对于Atari游戏而言，这是一个高维状态输入（原始图像），低维动作输出（上下左右）。我们只需要对高维状态进行降维，而不需要对动作也进行降维处理。

处理方法是只把状态s作为输入，但是输出的时候输出每一个动作的Q值，也就是输出一个向量$[Q(s,a_1),Q(s,a_2),......,Q(s,a_n)]$，这里输出是一个值，只不过是包含了所有动作的Q值的向量而已。这样我们就只要输入状态s，而且还同时可以得到所有的动作Q值，也将更方便的进行Q-Learning中动作的选择与Q值更新。

② Q值神经网络化

我们用一个深度神经网络来表示这个函数$f$。
输入是经过处理的4个连续的84x84图像（处理方式是利用[1]提到的预处理方法）经过三个卷积层，两个全连接层，最后输出包含每一个动作Q值的向量。

③ DQN算法

神经网络的训练是一个最优化问题，最优化一个损失函数，目标是让损失函数最小化。基于Q-Learnning算法，我们把目标Q值作为标签，目标就是让Q值趋近于目标Q值。因此，DQN训练的损失函数就是$L(w)=E[(r+\gamma maxQ(s^{\prime },a^{\prime },w)-Q(s,a,w){)}^2]$。
确定了损失函数，确定了获取样本的方式。那么DQN的整个算法也就成型了。

④ DQN训练

通过Q-Learning获取无限量的训练样本，然后对神经网络进行训练。但是仅仅通过简单的梯度下降算法SGD，对于网络的训练效果较差，因此引入了一下两个概念：经验回放与目标网络。

（1）经验回放

经验池的功能主要是解决相关性及非静态分布问题。具体做法是把每个时间戳Agent与环境交互得到的转移样本$(s_t,a_t,r_t,s_{t+1})$储存到回放记忆单元，要训练时就随机拿出一些（minibatch）来训练。（其实就是将游戏的过程打成碎片存储，训练时随机抽取就避免了相关性问题）。

这样做可以减少经验浪费并减轻经验关联性对网络训练的影响
伪代码：NIPS 2013 DQN算法

（2）目标网络

在[2]Nature 2015版本的DQN中提出了这个改进，使用另一个网络（这里称为target_net）产生Target Q值。具体地，$Q(s,a,w_{t+1})$表示当前网络eval_net的输出，用来评估当前状态动作对的值函数；$Q(s,a,w_{t+1})$表示target_net的输出，代入上面求 Target Q 值的公式中得到目标Q值。根据上面的Loss Function更新eval_net的参数，每经过N轮迭代，将参数复制给target_net。

引入target_net后，再一段时间里目标Q值使保持不变的，一定程度降低了当前Q值和目标Q值的相关性，提高了算法稳定性。

伪代码：Nature 2015 DQN算法

3、Demo实现流程

① 项目架构

基于Pytorch框架进行开发，完成了对于Atari游戏Pong的训练。

主要文件：

Env.memory.py：经验池
Env.models.py：DQN神经网络搭建
Env.wrappers.py：图像预处理
Dqn.py：主程序入口

数据分析：

Pong_run：tensorboard文件
Log/DQN：训练轮数与得分记录

② 训练参数

1.parser = argparse.ArgumentParser()  
2.parser.add_argument('--device', type=str,  
3.                    default='cuda' if torch.cuda.is_available() else 'cpu')  
4.parser.add_argument('--batch-size', type=int, default=32)  
5.parser.add_argument('--seed', type=int, default=0)  
6.parser.add_argument('--gamma', type=float, default=0.99)  
7.parser.add_argument('--eps-start', type=float, default=0.8)  
8.parser.add_argument('--eps-end', type=float, default=0.02)  
9.parser.add_argument('--eps-decay', type=int, default=1000000)  
10.parser.add_argument('--target-update', type=int, default=1000)  
11.parser.add_argument('--lr', type=float, default=0.0001)  
12.parser.add_argument('--initial-memory', type=int, default=500)  
13.parser.add_argument('--train-episodes', type=int, default=1600)  
14.parser.add_argument('--render-train', default=False,  
15.                    action="store_true", help="Render the Training Process")  
16.parser.add_argument('--render-test', default=False,  
17.                    action="store_true", help="Render the Testing Process")  
18.args = parser.parse_known_args()[0]  
19.args.memory_size = 200000 

③ DQN整体思路

1.def train(args, env, n_episodes, render=True):
2.    render = True
3.    writer_path = os.path.join('pong_runs', 'dqn_' + args.a_path)
4.    writer = SummaryWriter(writer_path)
5.    episode_list = []
6.    reward_list = []
7.    for episode in range(n_episodes):
8.        obs = env.reset()
9.        state = get_state(obs)
10.        total_reward = 0.0
11.        for t in count():
12.
13.            action = select_action(args, state)
14.            obs, reward, done, info = env.step(action)
15.
16.            if render:
17.                env.render()
18.
19.            total_reward += reward
20.
21.            if not done:
22.                next_state = get_state(obs)
23.            else:
24.                next_state = None
25.
26.            reward = torch.tensor([reward], device=args.device)
27.
28.            args.memory.push(state, action.to('cpu'),
29.                             next_state, reward.to('cpu'))
30.            state = next_state
31.
32.            if args.steps_done > args.initial_memory:
33.                optimize_model(args)
34.                if args.steps_done % args.target_update == 0:
35.                    args.target_net.load_state_dict(
36.                        args.policy_net.state_dict())
37.
38.            if done:
39.                episode_list.append(episode)
40.                reward_list.append(total_reward)
41.                break
42.
43.        # 写入tensorboard用于看图
44.        writer.add_scalar("reward", total_reward, episode)
45.        # 将每局对应的总奖励写成txt文件，用于matplotlib画图
46.        write_file(args.path+'/episodes.txt', episode_list)
47.        write_file(args.path+'/rewards.txt', reward_list)
48.
49.        if episode % 10 == 0 or episode == n_episodes-1:
50.            print('Total steps: {} \t Episode/t: {}/{} \t Total reward: {}'.format(
51.                args.steps_done, episode, t, total_reward))
52.    env.close()
53.    return

④ 经验池

1.class ReplayMemory(object):
2.    def __init__(self, capacity):
3.        self.capacity = capacity
4.        self.memory = []
5.        self.position = 0
6.        
7.    def push(self, *args):
8.        if len(self.memory) < self.capacity:
9.            self.memory.append(None)
10.        self.memory[self.position] = Transition(*args)
11.        self.position = (self.position + 1) % self.capacity
12.        
13.    def sample(self, batch_size):
14.        return random.sample(self.memory, batch_size)
15.    
16.    def __len__(self):
17.        return len(self.memory)

⑤ 神经网络搭建

1.class DQN(nn.Module):
2.    def __init__(self, in_channels=4, n_actions=14):
3.        super(DQN, self).__init__()
4.        self.conv1 = nn.Conv2d(in_channels, 32, kernel_size=8, stride=4)# 4*84*84-->32*20*20
5.        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)# 32*20*20-->64*9*9
6.        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)# 64*9*9-->64*7*7
7.
8.        self.fc4 = nn.Linear(7 * 7 * 64, 512)
9.        self.head = nn.Linear(512, n_actions)
10.        
11.    def forward(self, x):
12.        x = x.float() #/ 255
13.        x = F.relu(self.conv1(x)) 
14.        x = F.relu(self.conv2(x))
15.        x = F.relu(self.conv3(x))
16.
17.        x = F.relu(self.fc4(x.view(x.size(0), -1)))
        return self.head(x)

四、研究结果与项目结论

1、项目一

为了更好的展示训练的结果，我们设置了一个情景，即小人走迷宫。

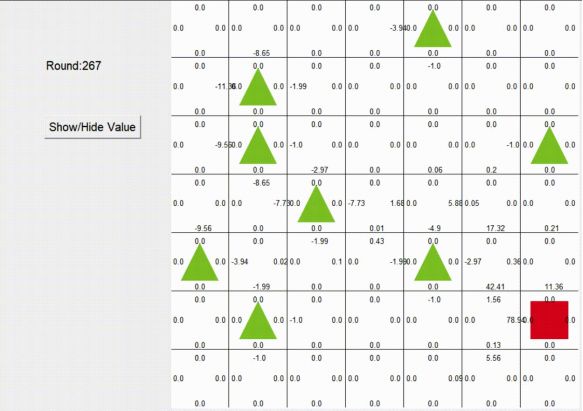
在上图的迷宫中，红色方框代表小人（我们的agent），绿色三角为迷宫中的障碍物，小人（我们的agent）碰到就会死亡，蓝色圆圈代表迷宫的终点，到达即获胜。

程序最开始运行时小人会经常撞到绿色三角障碍物上；300轮训练后，大致可以找到走出迷宫的路径。1000轮训练结束后，基本上已经找到了走出迷宫的路径。

此外，也可以见地图上每个格子的四个方位上都存在有一个数值，该数值就是我们的Q值，值越大agent在这个位置时选择走这个方向的概率就更大。经过1000轮训练后我们可以发现，存在一条路径中Q值远大于其他路径Q值的路，这即为找到的走出迷宫的路。

2、项目二

我们使用弹球游戏对训练结果进行测试。

我们控制右侧的绿色板子，电脑控制另一块橙色板子。小球从屏幕中央弹出，通过移动一侧板子将小球弹给对方。当一方未接到由另一方弹来的小球，即判负，为对手加上一分。我们设定当一方达到20分时为一轮。进行多轮次的训练。由于训练过程时间消耗很大，我们使用Tensorboard进行训练结果的可视化。当训练刚开始时，绿方完全不能接住弹出的小球，前几轮几乎橙色方得20分，绿方得0分。训练运行一段时间后，橙色方得分仍为20分，但绿色方得分变多。训练再运行一段时间后，逐渐打平。运行很长时间后，橙色方几乎不得分，绿色方可以完美接到橙色方弹出的小球。

利用Tensorboard对训练结果进行可视化，可得到如下曲线。

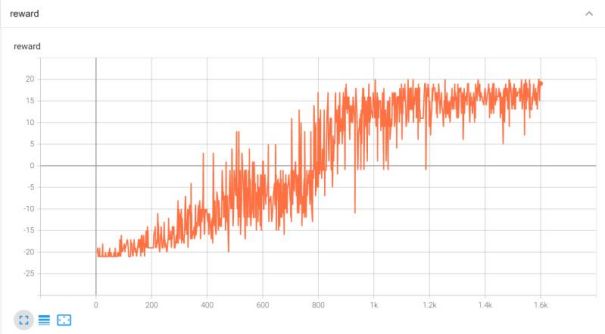
对曲线进行平滑处理后，可以得到如下训练曲线：

可以看出，随着训练时间的增长，橙色方得分逐渐增加，当训练到第800轮时基本打平。当训练到第1600轮时，橙色方几乎不得分。

参考文献

项目一：
[1] https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/tabular-q2/

[2] https://www.bilibili.com/video/BV13W411Y75P?p=8

[3] https://blog.csdn.net/sinat_32485497/article/details/75313499

[4] https://blog.csdn.net/qq_30615903/article/details/80739243

项目二：
[1] Mnih, Volodymyr, et al. “Playing atari with deep reinforcement learning.” arXiv preprint arXiv:1312.5602 (2013).

[2] Mnih V., Kavukcuoglu K., Silver D., et al. Human-level control through deep reinforcement learning. Nature,2015,518(7540):529-533.

[3] Haodi Zhang, Zihang Gao, Yi Zhou, et al. Faster and Safer Training by Embedding High-Level Knowledge into Deep Reinforcement Learning. arXiv preprint. 2019:1910.09986.

[4] Shusen Wang DQN高级技巧 https://www.youtube.com/watch?v=rhslMPmj7SY&list= PLvOO0btloRntS5U8rQWT9mHFcUdYOUmIC

[5] Hung-yi Lee DRL Lecture https://www.youtube.com/watch?v=o_g9JUMw1Oc

[6] 莫凡Python 强化学习 https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/

[7] Shusen Wang CS583：DeepLearning https://github.com/wangshusen/DeepLearning